🐠 🍖 👸🏽 Cómo hacer predicciones científicas. 👈🏾 🔐 🙇🏻

Predicciones, no casualidades

¿Cómo hacer predicciones de cualquier evento para que los científicos serios te crean, te vuelvas famoso y obtengas un Nobel? Es muy simple: debe convencer a los científicos de que sus predicciones son solo predicciones, no casuales. Un curso escolar en teoría de la probabilidad es suficiente para esto. Por lo tanto, solo se necesitan completar tres puntos.

Punto 1. Describamos el evento predicho, limitándolo al tiempo y al intervalo espacial. Por ejemplo, argumentamos que un determinado evento ocurrirá al día siguiente (intervalo de tiempo) dentro de los 100 km (intervalo espacial).

Luego, necesitamos calcular la probabilidad de una ocurrencia accidental de este evento en el intervalo especificado. Existen varios métodos para esto, dependiendo del tipo de eventos, su distribución, etc. Pero esto debe hacerse, y para esto indicamos un tiempo claro e intervalo espacial del evento. Denota esta probabilidad por P _chance.

TentaciónEn este punto, realmente quiero hacer trampa, declarando un intervalo igual al infinito. Es decir, este evento en el otro lado de la Tierra: cometimos un pequeño error en las coordenadas, pero el hecho de que sea un año después es un error en el tiempo. Pero, por desgracia, esta es exactamente la razón por la que necesitamos una evaluación de la ocurrencia aleatoria. En el caso de un intervalo infinito, será demasiado cercano a 1.

Punto 2. A continuación, veremos cuántos de los eventos predichos ocurrieron. Y en base a esto, calcularemos la probabilidad de nuestras predicciones. Es decir, si en el intervalo indicado el evento realmente sucedió, ponga un más, no sucedió - cero, y así para todas nuestras predicciones. Denote esta probabilidad P _antes.

TentaciónA veces, un evento no cae dentro de nuestro rango. Más una hora, menos un kilómetro. Y realmente quiero contarlo como una coincidencia. Muchos investigadores sin escrúpulos lo hacen. Pero no, necesitamos expandir inicialmente el rango de predicciones, o descartar nuestro evento del conteo como no exitoso.

Dilema: Y hay un dilema tan interesante: si aumentamos el rango, caerán más eventos predichos. Pero, la probabilidad de coincidencia accidental aumentará. Reducción del rango: disminuimos la precisión de nuestras predicciones.

Análisis de evaluación A continuación, puede realizar un análisis de evaluación del _caso P. y P _prev.Si la probabilidad de un evento accidental es mucho mayor de lo previsto, o son aproximadamente iguales, entonces estamos haciendo algo mal. Engaño, hechos apropiados, pero no predicciones. Si el _caso P. mucho menos que 1, y P _antes.más de al menos 0.5, entonces podemos decir que el estudio fue exitoso. Luego, necesitamos construir estimaciones probabilísticas más precisas, luego escribir artículos y postular al Nobel. Se completará el análisis de evaluación.

¿Te parece que este artículo no trata de nada, y todo esto es obvio para el investigador? Pero, por desgracia, la investigación que hice a continuación muestra un completo malentendido de estas cosas por parte de personas oficialmente dedicadas a la ciencia.

Segunda parte: predicción de terremotos

Pasamos al estudio de la fiabilidad de las predicciones de terremotos. La discusión que comenzó en los comentarios de esta publicación me animó a escribir este artículo . La esencia es esta: cierto equipo de científicos cree que puede predecir terremotos, y uno de los autores incluso pone estas predicciones en el sitio . Me comprometí a verificar la fiabilidad desde un punto de vista estadístico.

Para comenzar, la complejidad surgió con los límites de las predicciones: el autor no indica directamente en ningún lugar en qué rango se realiza. Es decir, ¿cómo entender que este evento es exactamente lo que predijimos? No hay respuesta en artículos científicos. Además, el gráfico de precisión de las predicciones muestra que los autores consideran que los eventos que ocurrieron a lo largo de 1000 km son predicciones exitosas. desde el punto predicho.

Pero podemos determinar los límites nosotros mismos. Para hacer esto, tome estas citas de sus artículos científicos :

El epicentro del terremoto, hasta ahora, incluye un área con un radio de unos 50 km.

Vemos que el error en grados (esto es aproximadamente 100 km) es una precisión bastante aceptable en las coordenadas. Esto se confirma en la tabla anterior. Para el intervalo de tiempo, tome el día según la siguiente cita:

El momento del inicio del supuesto terremoto podría variar dentro de ± 13 horas desde el tiempo estimado. De los 1,118 pronósticos, 978 casos se hicieron realidad el día en que fueron pronosticados;

Según los autores, la precisión alegada de tal pronóstico:

El éxito de estos pronósticos es del 70 al 80%.

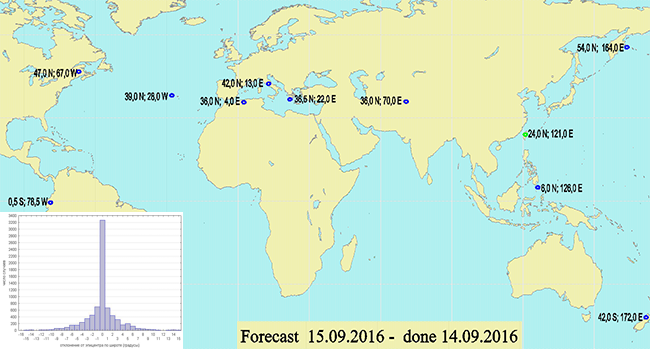
Evaluación independiente del pronóstico.

La evaluación se realizó el 15 de septiembre de 2016 (pude verificar que el pronóstico realmente apareció un día antes del evento y no ha cambiado desde entonces). Para no crear una carga en el sitio del autor, adjunto una imagen con un pronóstico.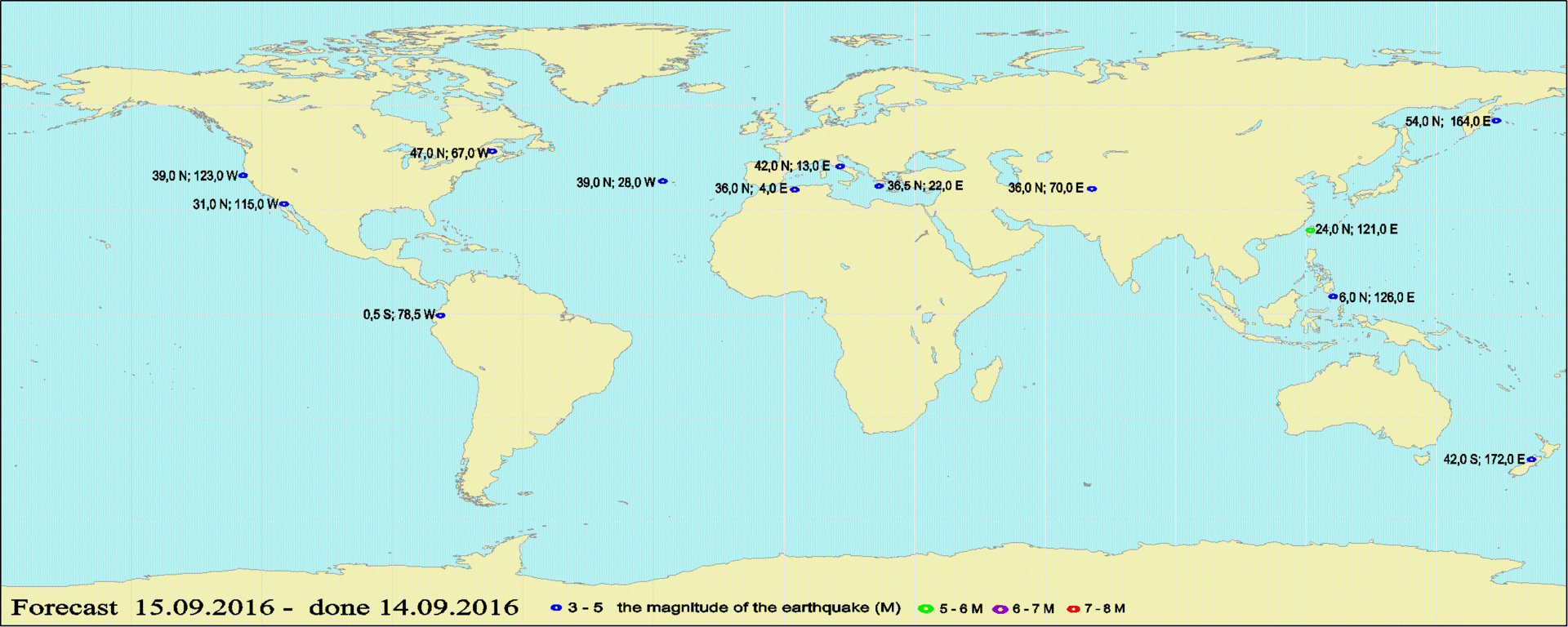

Los datos reales se tomaron del sitio web del EMSC
, el cual tiene la oportunidad de ver todos los terremotos durante cualquier período de tiempo, con ciertas magnitudes. Los datos pueden descargarse en forma de CSV o superponerse en un mapa de Google:

vemos una discrepancia completa de datos.Los datos se tomaron para el 15 de septiembre, se seleccionaron todos los eventos con una magnitud superior a 3. Si comparamos estas imágenes, veremos que los focos no coinciden en decenas de grados. Allí ni siquiera tiene que profundizar en los cálculos, a partir de los dibujos, por lo que todo está claro. Pero puedes hacer un pequeño análisis extra. En la tabla de la columna izquierda están los datos pronosticados, a la derecha, las coordenadas del epicentro más cercano, si el epicentro está más cerca de una docena de grados del punto predicho.

Predicho	Real
24N 121E (grande)
39N 123W
31N 115W
47N 67W
0.5S 78.5W	3.34S 80.8W
39N 28W
42N 13E	42.8N 13.2E
36N 4E
36.5N 22E	40.1N 24.8E
36N 70E
54N 164E
6N 126E	3.8N 129.1E
42S 172E

De los 13 eventos (uno de ellos es fuerte), solo 4 ocurrieron dentro de 1000 km. desde el punto indicado, y solo uno cabe en el cuadrado reclamado de 50 km.

¿Algo coincidió?

¡Pero uno de ellos coincidió con el grado! ¿Ha pasado algo? No, todo es más simple; no se ajusta al azar. Como se puede ver en la tabla Nie de los terremotos reales, se sacudió todos los días, comenzando el 10 de septiembre. Por lo tanto, la probabilidad de un evento en el punto indicado para el 15 de septiembre era demasiado cercana a 1.

Fecha	Latitud	Longitud	Magnitud
15/09/2016	42,82	13,19	4.3 4.3
14/09/2016	42,73	13,18	3.2
13/09/2016	42,58	13,2	3.4
12/09/2016	42,8	13,22	3.2
11/09/2016	42,68	13,28	3,3
10/09/2016	42,79	13,24	3.1
10/09/2016	42,96	13,16	3,3
10/09/2016	42,84	13,26	3

Debido a la aparente discrepancia entre las dos imágenes: terremotos pronosticados y reales, no hay ninguna razón para realizar un análisis más detallado, podemos llegar a conclusiones.

Conclusión

A juzgar por las estadísticas, las predicciones de estos científicos no tienen poder. Quien engaña exactamente a los autores, personas o ellos mismos, sigue siendo desconocido. Pero sus gráficos, en los que muestran la precisión de las predicciones, no son ciertos.

Lo que, de hecho, se correlaciona bien con el trabajo de los científicos del USGS que, en trabajos recientes, demostraron la imposibilidad de pronósticos a corto plazo, ya que el sistema es caótico, debido a la compleja estructura de la corteza terrestre, la perturbación crece exponencialmente. Es como con un montón de arena: rociando un grano de arena, sabemos que tarde o temprano la colina se derrumbará (se hacen pronósticos a largo plazo (años, décadas)), pero no sabemos cuándo sucederá exactamente (a corto plazo (día y hora) no son posibles). Más y más interesantemente escrito aquí , en la sección "Lecciones del pasado, dudas y esperanzas para el futuro".

Cómo hacer predicciones científicas.

Segunda parte: predicción de terremotos

More articles: