Cómo cortar un pastel con justicia
Los informáticos han desarrollado un algoritmo de pastel justo para cualquier número de personas.
 Dos jóvenes científicos, expertos en el campo de la informática, descubrieron cómo compartir honestamente un pastel entre cualquier número de personas, resolviendo el problema que los matemáticos han estado luchando durante décadas. Su trabajo sorprendió a muchos investigadores que consideraron esa separación imposible en principio.Compartir un pastel es una metáfora de una amplia gama de tareas de la vida real, incluida la división de un determinado objeto continuo, ya sea un pastel o un pedazo de tierra, entre personas que valoran sus propiedades de manera diferente. A uno le gusta una capa de chocolate, el otro quiere flores de color crema. Desde tiempos bíblicos, se conoce un algoritmo para dividir dicho objeto entre dos personas, de modo que nadie envidie a la otra: una persona divide el pastel en dos partes iguales para él, y la otra elige una de ellas. En Génesis, Abraham (entonces conocido como Abram) y Lot usaron este método para dividir la tierra, cuando Abraham inventó una separación, y Lot eligió entre Jordania y Canaán.En la década de 1960, los matemáticos idearon un algoritmo para tal pastel dividido "sin envidia" para tres personas. Pero hasta ahora, la mejor solución del problema para muchas personas era más de tres procedimientos establecidos en 1995, el politólogo Stephen Brahms [Steven Brams] de la Universidad de Nueva York y el matemático Alan Taylor [Alan] Taylor de la Universidad Union. Garantizó un reparto "justo" del pastel, pero con una condición: el procedimiento era "ilimitado", es decir, el número de pasos necesarios para compartir sería arbitrariamente grande.El algoritmo de Brahms-Taylor una vez se llamó avance, pero "es ilimitado, en mi opinión, fue un gran inconveniente", dice Ariel Procaccia[Ariel Procaccia], un científico informático de la Universidad Carnegie Mellon, uno de los creadores de Spliddit , una herramienta gratuita en línea para un reparto equitativo de tareas, desde tareas domésticas hasta tarifas de alquiler compartidas.En los últimos 50 años, muchos matemáticos e informáticos, incluido Procaccia, se han convencido de que no existe un algoritmo justo limitado para dividir un pastel en n partes."Fue esta tarea la que me llevó al área de las divisiones equitativas", dice Walter Stromkvist.[Walter Stromquist], profesor de matemáticas en el Brin Mavre College de Pensilvania, que logró buenos resultados en el problema del reparto de pasteles en 1980. "Toda mi vida pensé que volvería a este problema en mi tiempo libre y probaría que tal extensión del resultado es imposible en principio". .Pero, en abril, dos especialistas en ciencias de la computación refutaron estas expectativas al publicar un algoritmo para compartir pastel justo con un horario de trabajo que depende del número de participantes en el intercambio y no de sus preferencias personales. Un científico, Simon Mackenzie , Ph.D. , de 27 años , de Carnegie Mellon, presentó su trabajo el 10 de octubre en la 57ª edición de los fundamentos anuales de informática de IEEE.El algoritmo es extremadamente complejo. Una partición de pastel entre n participantes puede requerir hasta nn n n n n pasos, con aproximadamente el mismo número de cortes. Incluso para un pequeño número de participantes, este número excede el número de átomos en el universo. Pero los investigadores ya tienen ideas para simplificar y acelerar el algoritmo, según un segundo miembro del equipo, Haris Aziz , un especialista en informática de 35 años de la Universidad de Nueva Gales del Sur, que trabaja en el grupo de investigación de datos australiano Data61.Los expertos que estudian la teoría de la división equitativa , según Procaccia, consideran que "definitivamente es el mejor resultado durante décadas".
Dos jóvenes científicos, expertos en el campo de la informática, descubrieron cómo compartir honestamente un pastel entre cualquier número de personas, resolviendo el problema que los matemáticos han estado luchando durante décadas. Su trabajo sorprendió a muchos investigadores que consideraron esa separación imposible en principio.Compartir un pastel es una metáfora de una amplia gama de tareas de la vida real, incluida la división de un determinado objeto continuo, ya sea un pastel o un pedazo de tierra, entre personas que valoran sus propiedades de manera diferente. A uno le gusta una capa de chocolate, el otro quiere flores de color crema. Desde tiempos bíblicos, se conoce un algoritmo para dividir dicho objeto entre dos personas, de modo que nadie envidie a la otra: una persona divide el pastel en dos partes iguales para él, y la otra elige una de ellas. En Génesis, Abraham (entonces conocido como Abram) y Lot usaron este método para dividir la tierra, cuando Abraham inventó una separación, y Lot eligió entre Jordania y Canaán.En la década de 1960, los matemáticos idearon un algoritmo para tal pastel dividido "sin envidia" para tres personas. Pero hasta ahora, la mejor solución del problema para muchas personas era más de tres procedimientos establecidos en 1995, el politólogo Stephen Brahms [Steven Brams] de la Universidad de Nueva York y el matemático Alan Taylor [Alan] Taylor de la Universidad Union. Garantizó un reparto "justo" del pastel, pero con una condición: el procedimiento era "ilimitado", es decir, el número de pasos necesarios para compartir sería arbitrariamente grande.El algoritmo de Brahms-Taylor una vez se llamó avance, pero "es ilimitado, en mi opinión, fue un gran inconveniente", dice Ariel Procaccia[Ariel Procaccia], un científico informático de la Universidad Carnegie Mellon, uno de los creadores de Spliddit , una herramienta gratuita en línea para un reparto equitativo de tareas, desde tareas domésticas hasta tarifas de alquiler compartidas.En los últimos 50 años, muchos matemáticos e informáticos, incluido Procaccia, se han convencido de que no existe un algoritmo justo limitado para dividir un pastel en n partes."Fue esta tarea la que me llevó al área de las divisiones equitativas", dice Walter Stromkvist.[Walter Stromquist], profesor de matemáticas en el Brin Mavre College de Pensilvania, que logró buenos resultados en el problema del reparto de pasteles en 1980. "Toda mi vida pensé que volvería a este problema en mi tiempo libre y probaría que tal extensión del resultado es imposible en principio". .Pero, en abril, dos especialistas en ciencias de la computación refutaron estas expectativas al publicar un algoritmo para compartir pastel justo con un horario de trabajo que depende del número de participantes en el intercambio y no de sus preferencias personales. Un científico, Simon Mackenzie , Ph.D. , de 27 años , de Carnegie Mellon, presentó su trabajo el 10 de octubre en la 57ª edición de los fundamentos anuales de informática de IEEE.El algoritmo es extremadamente complejo. Una partición de pastel entre n participantes puede requerir hasta nn n n n n pasos, con aproximadamente el mismo número de cortes. Incluso para un pequeño número de participantes, este número excede el número de átomos en el universo. Pero los investigadores ya tienen ideas para simplificar y acelerar el algoritmo, según un segundo miembro del equipo, Haris Aziz , un especialista en informática de 35 años de la Universidad de Nueva Gales del Sur, que trabaja en el grupo de investigación de datos australiano Data61.Los expertos que estudian la teoría de la división equitativa , según Procaccia, consideran que "definitivamente es el mejor resultado durante décadas".Pedazos de pastel
El algoritmo de Aziz y Mackenzie se basa en un procedimiento elegante inventado independientemente por los matemáticos John Selfridge y John Conway en la década de 1960, que le permite dividir un pastel en tres.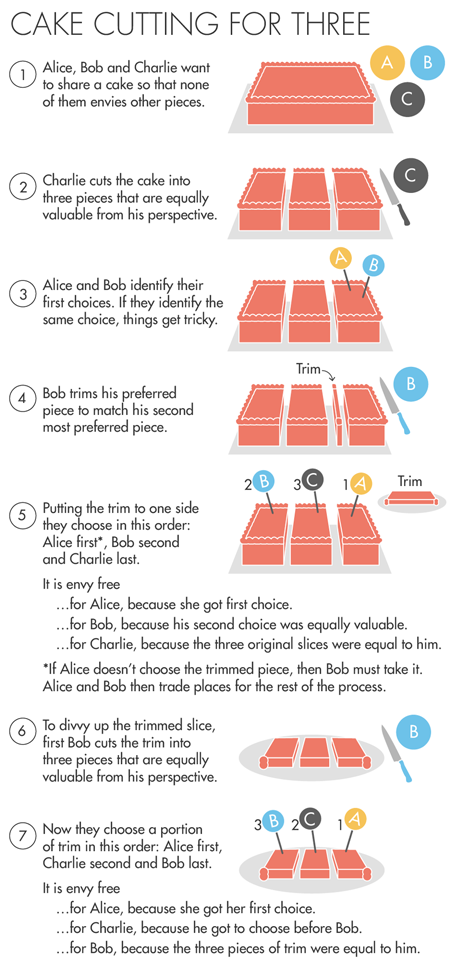 Si Alice, Bob y Charlie (A, B, C) quieren dividir el pastel, el algoritmo comienza con Charlie dividiendo el pastel en tres pedazos que le parecen iguales. Alice y Bob eligen las piezas que les gustan. Si eligen diferentes piezas, voila, todos obtienen lo que quieren.Si Alice y Bob eligen una pieza, entonces Bob corta una pequeña parte de esta pieza para que la pieza se vuelva equivalente, en su opinión, a otro pedazo de pastel, el que Bob elegiría en segundo lugar. El residuo cortado se pospone. Ahora Alice debe elegir la mejor pieza para ella de las tres restantes, y luego selecciona a Bob, con la condición de que él tome la pieza cortada por él, si Alice no la selecciona. Charlie consigue la tercera pieza.Como resultado, nadie envidia a nadie. Alice eligió el primero. Bob recibió una de dos piezas de igual valor para él. Charlie consiguió una de las tres piezas originales que él mismo cortó.Solo queda un pequeño corte. Pero se puede dividir sin iniciar primero el algoritmo y sin caer en un ciclo interminable de circuncisiones y elecciones, ya que Charlie está satisfecho con su pieza, e incluso si el que obtuvo la pieza recortada recibiría el resto completo en apéndice, por Charlie no se vería deshonesto, porque la pieza cortada y el resto le darán un pedazo de pastel equivalente a su pieza; después de todo, cortó estas piezas desde el principio. Aziz y Mackenzie describen la posición de Charlie como "dominante".Ahora, si, por ejemplo, Alice obtuvo la pieza cortada, entonces Bob corta la moldura en tres partes, equivalente desde su punto de vista, Alice selecciona una de estas piezas para sí misma, luego selecciona a Charlie y luego a Bob. Todos están contentos: Alice eligió primero, Charlie obtiene una pieza mejor que Bob (y no le importa cuánto tomó Alice), y desde el punto de vista de Bob, las tres piezas son equivalentes.Brahms y Taylor usaron la propiedad de "dominio" (pero con un nombre diferente) para desarrollar su algoritmo de 1995, pero no terminaron su idea hasta que apareció un algoritmo limitado. En los próximos 20 años, nadie ha logrado los mejores resultados. "Y no por la falta de intentos", dice Procaccia.
Si Alice, Bob y Charlie (A, B, C) quieren dividir el pastel, el algoritmo comienza con Charlie dividiendo el pastel en tres pedazos que le parecen iguales. Alice y Bob eligen las piezas que les gustan. Si eligen diferentes piezas, voila, todos obtienen lo que quieren.Si Alice y Bob eligen una pieza, entonces Bob corta una pequeña parte de esta pieza para que la pieza se vuelva equivalente, en su opinión, a otro pedazo de pastel, el que Bob elegiría en segundo lugar. El residuo cortado se pospone. Ahora Alice debe elegir la mejor pieza para ella de las tres restantes, y luego selecciona a Bob, con la condición de que él tome la pieza cortada por él, si Alice no la selecciona. Charlie consigue la tercera pieza.Como resultado, nadie envidia a nadie. Alice eligió el primero. Bob recibió una de dos piezas de igual valor para él. Charlie consiguió una de las tres piezas originales que él mismo cortó.Solo queda un pequeño corte. Pero se puede dividir sin iniciar primero el algoritmo y sin caer en un ciclo interminable de circuncisiones y elecciones, ya que Charlie está satisfecho con su pieza, e incluso si el que obtuvo la pieza recortada recibiría el resto completo en apéndice, por Charlie no se vería deshonesto, porque la pieza cortada y el resto le darán un pedazo de pastel equivalente a su pieza; después de todo, cortó estas piezas desde el principio. Aziz y Mackenzie describen la posición de Charlie como "dominante".Ahora, si, por ejemplo, Alice obtuvo la pieza cortada, entonces Bob corta la moldura en tres partes, equivalente desde su punto de vista, Alice selecciona una de estas piezas para sí misma, luego selecciona a Charlie y luego a Bob. Todos están contentos: Alice eligió primero, Charlie obtiene una pieza mejor que Bob (y no le importa cuánto tomó Alice), y desde el punto de vista de Bob, las tres piezas son equivalentes.Brahms y Taylor usaron la propiedad de "dominio" (pero con un nombre diferente) para desarrollar su algoritmo de 1995, pero no terminaron su idea hasta que apareció un algoritmo limitado. En los próximos 20 años, nadie ha logrado los mejores resultados. "Y no por la falta de intentos", dice Procaccia.Divisores de pastel no profesionales
Cuando Aziz y Mackenzie (A&M) decidieron asumir esta tarea hace un par de años, eran nuevos en la tarea de compartir pasteles. "No teníamos tanta experiencia como las personas que trabajaron intensamente en él", dijo Aziz. "Aunque esto suele ser un inconveniente, en nuestro caso fue una ventaja, porque pensamos de manera diferente".A&M comenzó estudiando la tarea de dividir en tres participantes desde cero, y como resultado del análisis llegó a un algoritmo justo limitado para cuatro participantes , publicado por ellos el año pasado.No pudieron mostrar de inmediato cómo expandir su algoritmo a un número mayor de cuatro participantes, pero asumieron esta tarea con entusiasmo. "Después de enviar el trabajo sobre cuatro participantes, realmente queríamos continuar rápidamente el trabajo hasta que alguien más experimentado e inteligente lo generalizara independientemente al caso de n participantes", dice Aziz. Y después de aproximadamente un año, su búsqueda fue exitosa.Al igual que el algoritmo Selfridge-Conway, el protocolo AiM ofrece constantemente diferentes participantes para cortar el pastel en n partes iguales, y otros para cortar y elegir pedazos de pastel. Pero hay otros pasos en el algoritmo, por ejemplo, el intercambio periódico de piezas de pasteles de una manera especial, con el fin de aumentar el número de relaciones dominantes entre los participantes.Estas relaciones permiten a A&M reducir la complejidad de la tarea. Si, por ejemplo, tres participantes dominan al resto, ya pueden ser enviados a comer sus propios pedazos de pastel; estarán felices independientemente de quién reciba las sobras. Después de esto, quedan menos participantes, y después de un número limitado de tales pasos, todos están satisfechos y todo el pastel se divide."Mirando hacia atrás a la complejidad del algoritmo, no sorprende que haya tardado tanto en desarrollarlo", dice Procaccia. Pero A&M ya cree que pueden simplificar el algoritmo para que no requiera un intercambio de piezas y tenga lugar en solo n n n pasos. Según Aziz, ya están trabajando en estos resultados.Brahms advierte que incluso un algoritmo más simple no tendrá una aplicación práctica; después de todo, los pedazos de pastel recibidos por los participantes incluirán muchas migajas pequeñas de diferentes partes del pastel. Este enfoque no es particularmente útil si, por ejemplo, está dividiendo la tierra.Pero para los matemáticos y los informáticos que estudian el problema, el nuevo resultado "restablece todo el tema", dice Stromkvist.Ahora que los investigadores saben que la torta se puede dividir en un número limitado de pasos, el siguiente paso, según Procaccia, es comprender la gran brecha entre el límite superior en el número de pasos por el método AiM y el límite inferior en el número de pasos necesarios para esto. Procaccia ya ha demostrado anteriormente que el algoritmo para la separación equitativa del pastel no puede pasar en menos de n2 pasos, pero el número de pasos es pequeño en comparación con n n n n n n e incluso n n n .Aziz dice que los investigadores ahora tienen que descubrir cómo reducir esta brecha. "Creo que se puede avanzar en ambas direcciones".Source: https://habr.com/ru/post/es398683/
All Articles