La belleza de los números. Constantes matemáticas en la naturaleza

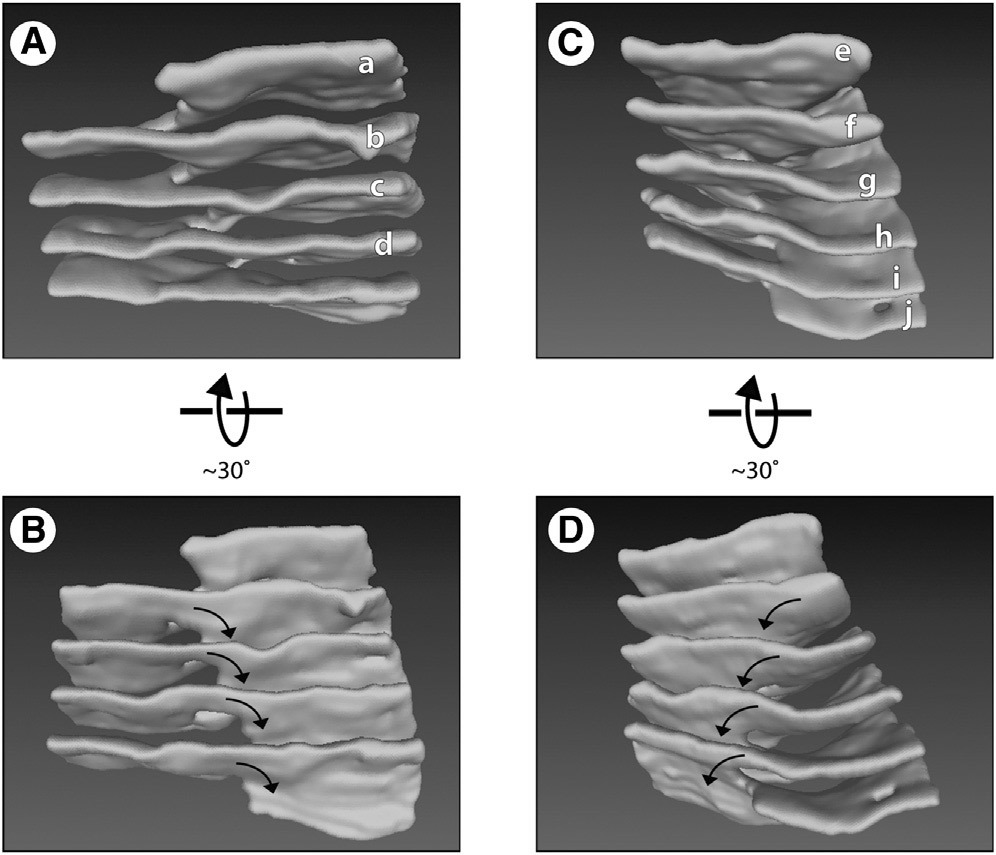Un modelo 3D del retículo endoplásmico de una célula eucariota con rampas de Terasaki que conectan las láminas planas de la membrana

En 2013, un grupo de biólogos moleculares de los Estados Unidos investigó una forma muy interesante del retículo endoplásmico : el organoide dentro de la célula eucariota. La membrana de este organoide consta de láminas planas conectadas por "rampas" en espiral, como si se calculara en un programa de modelado 3D. Estas son las llamadas rampas de Terasaki. Tres años más tarde, el trabajo de los biólogos fue notado por los astrofísicos. Se sorprendieron: después de todo, precisamente tales estructuras están presentes dentro de las estrellas de neutrones. La llamada "pasta nuclear" consiste en láminas paralelas conectadas por formas espirales.

La sorprendente similitud estructural de las células vivas y las estrellas de neutrones: ¿de dónde vino? Obviamente, no existe una conexión directa entre las células vivas y las estrellas de neutrones. ¿Solo una coincidencia?


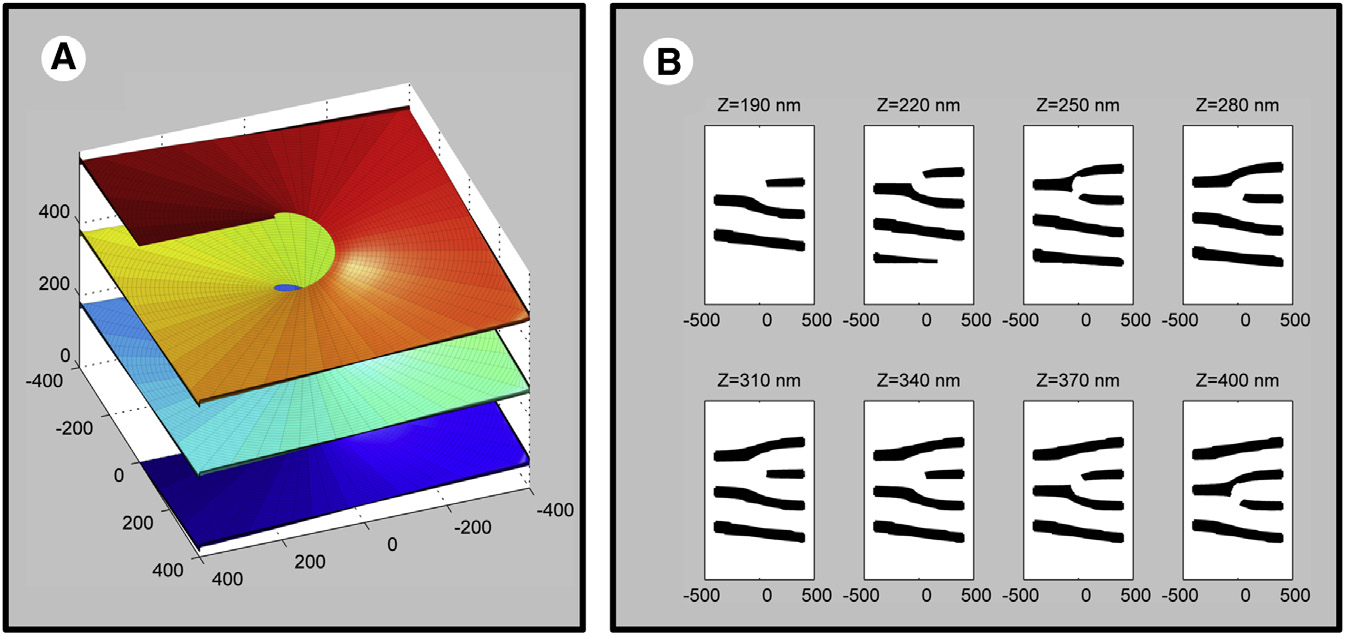Modelo de conexiones espirales entre láminas de membrana plana en una célula eucariota

Se supone que las leyes de la naturaleza actúan sobre todos los objetos del micro y macrocosmos de tal manera que algunas de las formas y configuraciones más óptimas aparecen como si fueran por sí mismas. En otras palabras, los objetos del mundo físico obedecen las leyes matemáticas ocultas que subyacen en todo el universo.

Veamos algunos ejemplos más que respaldan esta teoría. Estos son ejemplos donde objetos materiales esencialmente diferentes exhiben propiedades similares.

Por ejemplo, los agujeros negros acústicos, observados por primera vez en 2011, exhiben las mismas propiedades que los agujeros negros reales deberían tener en teoría. En el primer agujero negro acústico experimentalEl condensado de Bose-Einstein de 100 mil átomos de rubidio se desenroscó a una velocidad supersónica de tal manera que algunas partes del condensado cruzaron la barrera del sonido, mientras que las vecinas no lo hicieron. El límite de estas partes de condensado simulaba un horizonte de eventos de agujero negro, donde la velocidad del flujo es exactamente igual a la velocidad del sonido. A temperaturas cercanas al cero absoluto, el sonido comienza a comportarse como partículas cuánticas - fonones(una cuasipartícula ficticia representa un cuanto de movimiento vibratorio de los átomos de cristal). Resultó que un agujero negro de "sonido" absorbe partículas de la misma manera que un agujero negro real absorbe fotones. Por lo tanto, el flujo de fluido actúa sobre el sonido de la misma manera que un agujero negro real actúa sobre la luz. En principio, un agujero negro sónico con fonones puede considerarse como un modelo peculiar de curvatura verdadera en el espacio-tiempo.

Si observa más ampliamente las similitudes estructurales en varios fenómenos físicos, puede ver un orden sorprendente en el caos natural. Todos los fenómenos naturales diversos se describen, de hecho, mediante reglas básicas simples. Reglas matemáticas

Toma los fractales. Estas son formas geométricas auto-similares que se pueden dividir en partes para que cada parte sea al menos aproximadamente una copia reducida del todo. Un ejemplo es el famoso helecho Barnsley.



El helecho de Barnsley se construye utilizando cuatro transformaciones afines de la forma:



esta hoja en particular se genera con los siguientes coeficientes: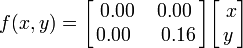









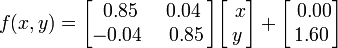
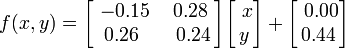en nuestro entorno, tales fórmulas matemáticas se encuentran en todas partes: en nubes, árboles, cadenas montañosas, cristales de hielo, llamas parpadeantes, en la costa del mar. Estos son ejemplos de fractales, cuya estructura se describe mediante cálculos matemáticos relativamente simples.

Galileo Galilei ya en 1623 dijo: "Toda la ciencia está escrita en este gran libro, me refiero al Universo, que siempre está abierto para nosotros, pero que no se puede entender sin aprender a entender el idioma en el que está escrito. Y está escrito en el lenguaje de las matemáticas, y sus letras son triángulos, círculos y otras figuras geométricas, sin las cuales es imposible para una persona distinguir cualquiera de sus palabras; sin ellos, es como vagar en la oscuridad ".

De hecho, las reglas matemáticas se manifiestan no solo en la geometría y los contornos visuales de los objetos naturales, sino también en otras leyes. Por ejemplo, en la dinámica no lineal de la población, cuya tasa de crecimiento disminuye dinámicamente al acercarse al límite natural del nicho ecológico. O en física cuántica.

En cuanto a las constantes matemáticas más famosas, por ejemplo, el número pi, es bastante natural que se encuentre ampliamente en la naturaleza, porque las formas geométricas correspondientes son las más racionales y adecuadas para muchos objetos naturales. En particular, el número 2π se convirtió en la constante física fundamental. Muestra cuál es el ángulo de rotación en radianes, que está contenido en una revolución completa cuando el cuerpo gira. En consecuencia, esta constante se encuentra en todas partes en la descripción de la forma rotacional del movimiento y el ángulo de rotación, así como en la interpretación matemática de las oscilaciones y las ondas.

Por ejemplo, el período de pequeñas vibraciones naturales de un péndulo matemático de longitud L inmóvil suspendido en un campo gravitacional uniforme con aceleración gravitacional g es



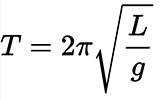Bajo condiciones de rotación de la Tierra, el plano de oscilación del péndulo rotará lentamente en la dirección opuesta a la dirección de rotación de la Tierra. La velocidad de rotación del plano de oscilación del péndulo depende de su latitud geográfica .



El número pi es una parte integral de la constante de Dirac : la constante de Planck reducida, la constante principal de la física cuántica, que conecta dos sistemas de unidades: cuántica y tradicional. Relaciona la magnitud de la energía cuántica de cualquier sistema físico oscilatorio lineal con su frecuencia.



En consecuencia, el número pi se incluye en el postulado fundamental de la mecánica cuántica: el principio de incertidumbre de Heisenberg.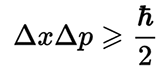



El número pi se usa en la fórmula constante de estructura fina- otra constante física fundamental que caracteriza la fuerza de la interacción electromagnética, así como en las fórmulas hidromecánicas, etc.

En el mundo natural, puedes encontrar otras constantes matemáticas. Por ejemplo, el número e , la base del logaritmo natural. Esta constante se incluye en la fórmula para la distribución de probabilidad normal, que viene dada por la función de densidad de probabilidad:



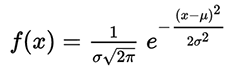la distribución normal está sujeta a muchos fenómenos naturales, incluidas muchas características de los organismos vivos en una población. Por ejemplo, la distribución del tamaño de los organismos en una población: longitud, altura, área de superficie, peso, presión arterial en humanos y mucho más.

Una observación cercana del mundo que nos rodea muestra que las matemáticas no son en absoluto una ciencia abstracta seca, como podría parecer a primera vista. Todo lo contrario. Las matemáticas son la base de todo el mundo viviente y no viviente. Como Galileo Galilei señaló correctamente, las matemáticas son el lenguaje que la naturaleza nos habla.

Source: https://habr.com/ru/post/es398987/