Calculadora de cartón y bola de cuatro bits.
 Apariencia de una calculadora de cartón de cartón de cuatro bits. El medio sumador en la parte superior y los tres sumadores en la parte media e inferior de la calculadora son claramente visibles.Érase una vez, antes de la invención de la electrónica, la gente fabricaba computadoras mecánicas con materiales improvisados. El ejemplo más famoso y complejo de tal máquina es el mecanismo anticitera : se usó un dispositivo complejo de al menos 30 engranajes para calcular el movimiento de los cuerpos celestes e hizo posible averiguar la fecha de 42 eventos astronómicos.Hoy en día, es más probable que las computadoras mecánicas (calculadoras) sean un objeto de entretenimiento para los geeks y una ocasión para organizar un espectáculo divertido. Por ejemplo, como una computadora de 10,000 fichas de dominó que suma números binarios arbitrarios de cuatro dígitos y produce una suma de dos bits de cinco dígitos (teoría matemática de esta calculadora y arquitectura ). Tales actuaciones permiten a los niños comprender mejor cómo funcionan las operaciones de lógica de bits en la programación y cómo se organizan las puertas lógicas. Y, en general, es muy interesante hacer una computadora pequeña con sus propias manos con materiales improvisados, especialmente si lo hace con su hijo.
Apariencia de una calculadora de cartón de cartón de cuatro bits. El medio sumador en la parte superior y los tres sumadores en la parte media e inferior de la calculadora son claramente visibles.Érase una vez, antes de la invención de la electrónica, la gente fabricaba computadoras mecánicas con materiales improvisados. El ejemplo más famoso y complejo de tal máquina es el mecanismo anticitera : se usó un dispositivo complejo de al menos 30 engranajes para calcular el movimiento de los cuerpos celestes e hizo posible averiguar la fecha de 42 eventos astronómicos.Hoy en día, es más probable que las computadoras mecánicas (calculadoras) sean un objeto de entretenimiento para los geeks y una ocasión para organizar un espectáculo divertido. Por ejemplo, como una computadora de 10,000 fichas de dominó que suma números binarios arbitrarios de cuatro dígitos y produce una suma de dos bits de cinco dígitos (teoría matemática de esta calculadora y arquitectura ). Tales actuaciones permiten a los niños comprender mejor cómo funcionan las operaciones de lógica de bits en la programación y cómo se organizan las puertas lógicas. Y, en general, es muy interesante hacer una computadora pequeña con sus propias manos con materiales improvisados, especialmente si lo hace con su hijo.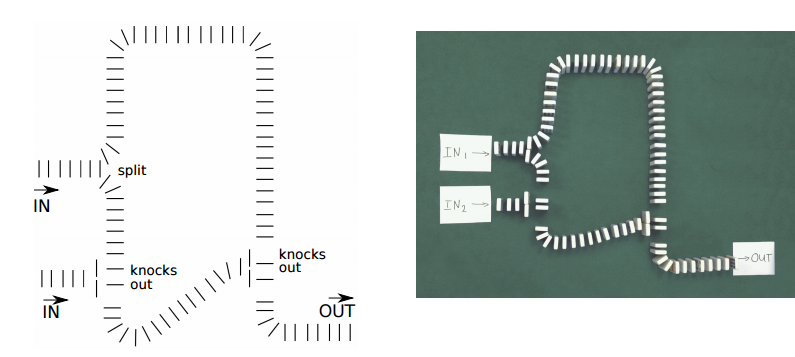 El funcionamiento lógico Y en una computadora de 10,000 fichas de dominó.Para la fabricación de una calculadora mecánica, el constructor de Lego es excelente. Puede encontrar muchos ejemplos de tales calculadoras en YouTube .Calculadora de computadora LegoInspirado en un ejemplo de una computadora hecha de dominó y calculadoras mecánicas del constructor de Lego, el programador de C ++ bajo el apodo de lapinozz, junto con sus hermanas menores, decidió construir en casa algo similar para uno de los proyectos de ciencias de la escuela de la hermana. Concibió e implementó una calculadora LOGIC de cuatro bits completamente funcional (Logic cardbOard Gates Inpredictable Calculator) . Para producir esta computadora, no se necesita nada más que cartón y pegamento, y no funciona con electricidad, sino con bolas y gravedad terrestre. La calculadora puede agregar números del 0 al 15 con un máximo de 30.A diferencia de las fichas de dominó de Lego y los ladrillos de Lego, no se utilizaron componentes de fábrica en la fabricación de esta calculadora. Todos los elementos de la calculadora están pegados de cartón desde cero, lo que se entiende bien a partir de las fotos del dispositivo. En este sentido, este dispositivo puede considerarse único.
El funcionamiento lógico Y en una computadora de 10,000 fichas de dominó.Para la fabricación de una calculadora mecánica, el constructor de Lego es excelente. Puede encontrar muchos ejemplos de tales calculadoras en YouTube .Calculadora de computadora LegoInspirado en un ejemplo de una computadora hecha de dominó y calculadoras mecánicas del constructor de Lego, el programador de C ++ bajo el apodo de lapinozz, junto con sus hermanas menores, decidió construir en casa algo similar para uno de los proyectos de ciencias de la escuela de la hermana. Concibió e implementó una calculadora LOGIC de cuatro bits completamente funcional (Logic cardbOard Gates Inpredictable Calculator) . Para producir esta computadora, no se necesita nada más que cartón y pegamento, y no funciona con electricidad, sino con bolas y gravedad terrestre. La calculadora puede agregar números del 0 al 15 con un máximo de 30.A diferencia de las fichas de dominó de Lego y los ladrillos de Lego, no se utilizaron componentes de fábrica en la fabricación de esta calculadora. Todos los elementos de la calculadora están pegados de cartón desde cero, lo que se entiende bien a partir de las fotos del dispositivo. En este sentido, este dispositivo puede considerarse único.Objetivo del proyecto
Representación visual de cómo agregar números binarios. Enseñar a un alumno a traducir de decimal a binario y viceversa. Estudio de operaciones lógicas de bits y circuitos lógicos básicos.Apariencia de la calculadora
Como puede ver en la fotografía de la calculadora, en la parte superior hay una zona para ingresar datos. Después de completar todas las operaciones lógicas, las bolas muestran el resultado de la operación a continuación. La entrada de datos se realiza por bolas. La bola es - 1, la bola no es - 0. El bit de la derecha es el bit más pequeño del número. Antes de comenzar a trabajar, algunas partes de la calculadora deben llevarse a su posición original. Después de especificar los valores iniciales, la tira de cartón se empuja hacia atrás, lo que mantiene las bolas en la posición inicial, y comienza el proceso de adición.Por ejemplo, esta es la posición inicial de las bolas para la operación 7 + 5 (0111 + 0101).
La entrada de datos se realiza por bolas. La bola es - 1, la bola no es - 0. El bit de la derecha es el bit más pequeño del número. Antes de comenzar a trabajar, algunas partes de la calculadora deben llevarse a su posición original. Después de especificar los valores iniciales, la tira de cartón se empuja hacia atrás, lo que mantiene las bolas en la posición inicial, y comienza el proceso de adición.Por ejemplo, esta es la posición inicial de las bolas para la operación 7 + 5 (0111 + 0101).
Dispositivo calculadora
Las operaciones lógicas de una calculadora de cartón se llevan a cabo de manera similar, como en la computadora de dominó mencionada anteriormente .Las puertas lógicas esquemáticas para todas las operaciones lógicas se muestran en el diagrama. Es decir, la puerta lógica "AND" (AND) significa que cuando se reciben 0 bolas en la entrada, se obtiene 0 en la salida. Al recibir 1 bola en la entrada, se obtiene 0 en la salida. Al recibir 2 bolas en la entrada, se obtiene 1 en la salida.1 en la entrada, 0 en la salida
Es decir, la puerta lógica "AND" (AND) significa que cuando se reciben 0 bolas en la entrada, se obtiene 0 en la salida. Al recibir 1 bola en la entrada, se obtiene 0 en la salida. Al recibir 2 bolas en la entrada, se obtiene 1 en la salida.1 en la entrada, 0 en la salida 2 en la entrada, 1 en la salida
2 en la entrada, 1 en la salida La puerta lógica XOR es un poco más complicada. En este caso, si llega una pelota, debe pasar. Y si llegan dos bolas, entonces deben cancelarse entre sí, es decir, el resultado será 0. El autor muestra cómo hacerlo, a través de un trozo de cartón que cuelga verticalmente con un cuello estrecho. Si dos bolas llegan al mismo tiempo, entonces se bloquean entre sí, y por lo tanto implementan efectivamente la operación lógica XOR.Puerta lógica XOR
La puerta lógica XOR es un poco más complicada. En este caso, si llega una pelota, debe pasar. Y si llegan dos bolas, entonces deben cancelarse entre sí, es decir, el resultado será 0. El autor muestra cómo hacerlo, a través de un trozo de cartón que cuelga verticalmente con un cuello estrecho. Si dos bolas llegan al mismo tiempo, entonces se bloquean entre sí, y por lo tanto implementan efectivamente la operación lógica XOR.Puerta lógica XOR Para optimizar el sistema y no bloquear la masa de las puertas lógicas AND y XOR, el autor implementó un medio sumador- un circuito lógico combinacional que tiene dos entradas y dos salidas. El medio sumador le permite calcular la suma de A + B, con el resultado de dos bits S y C, donde S es el bit de la suma del módulo 2 y C es el bit de acarreo. En nuestra construcción de cartón, esto significa que si tenemos 1 bola en la entrada, entonces va a la salida C, y si hay 2 bolas en la entrada, entonces 1 bola va a la salida S, y la segunda no llega a ninguna parte.El programador ideó un esquema bastante simple y efectivo para un medio sumador. En él, 1 bola en la entrada continúa tranquilamente su camino, girando la barrera y pasando al hoyo C. Pero si entran dos bolas, entonces la segunda bola ya no puede pasar a través de la barrera, volteada por la primera bola, y cae en el hoyo, clavando un nuevo camino S. Este es un medio sumador.Una pelota en la entrada del medio sumador
Para optimizar el sistema y no bloquear la masa de las puertas lógicas AND y XOR, el autor implementó un medio sumador- un circuito lógico combinacional que tiene dos entradas y dos salidas. El medio sumador le permite calcular la suma de A + B, con el resultado de dos bits S y C, donde S es el bit de la suma del módulo 2 y C es el bit de acarreo. En nuestra construcción de cartón, esto significa que si tenemos 1 bola en la entrada, entonces va a la salida C, y si hay 2 bolas en la entrada, entonces 1 bola va a la salida S, y la segunda no llega a ninguna parte.El programador ideó un esquema bastante simple y efectivo para un medio sumador. En él, 1 bola en la entrada continúa tranquilamente su camino, girando la barrera y pasando al hoyo C. Pero si entran dos bolas, entonces la segunda bola ya no puede pasar a través de la barrera, volteada por la primera bola, y cae en el hoyo, clavando un nuevo camino S. Este es un medio sumador.Una pelota en la entrada del medio sumador Dos bolas en la entrada del medio sumador
Dos bolas en la entrada del medio sumador Finalmente, el sumador es una verdadera obra maestra. Por lo general, se compone de dos medios sumadores y una puerta lógica "OR", pero el autor ha implementado otro diseño, que en realidad es una pequeña modificación del medio sumador.Una bola en la entrada - una bola en el camino 1
Finalmente, el sumador es una verdadera obra maestra. Por lo general, se compone de dos medios sumadores y una puerta lógica "OR", pero el autor ha implementado otro diseño, que en realidad es una pequeña modificación del medio sumador.Una bola en la entrada - una bola en el camino 1 Dos bolas en la entrada - una bola en el camino 2
Dos bolas en la entrada - una bola en el camino 2 Tres bolas en la entrada - una bola en el camino 1, y la otra a lo largo del camino 2
Tres bolas en la entrada - una bola en el camino 1, y la otra a lo largo del camino 2 La calculadora completa consiste enteramente en un medio sumador y tres sumadores.
La calculadora completa consiste enteramente en un medio sumador y tres sumadores. La calculadora da el resultado de cálculo correcto si las bolas caen a la velocidad correcta, ni demasiado rápido ni demasiado lento, y no rebotan entre sí. La lógica en sí es perfecta, pero en la práctica, la calculadora a veces tiene errores.
La calculadora da el resultado de cálculo correcto si las bolas caen a la velocidad correcta, ni demasiado rápido ni demasiado lento, y no rebotan entre sí. La lógica en sí es perfecta, pero en la práctica, la calculadora a veces tiene errores.Source: https://habr.com/ru/post/es399391/
All Articles