Estructuras misteriosas combinan matemática y naturaleza.

En la ciudad de Cuernavaca en México, una red "espía" aumenta la eficiencia de la flota de autobuses. Como resultado, el horario de salida del autobús siempre coincide con el patrón de "universalidad"

En 1999, mientras estaba sentado en una parada de autobús en Cuernavaca, México, el físico checo Petr Šeba notó que las personas le daban trozos de papel a los conductores de autobuses a cambio de dinero. Descubrió que esto no era una manifestación del crimen organizado, sino un comercio "oculto" diferente: cada conductor pagaba un "espía", y señalaba cuándo el autobús anterior partía de la parada. Si se fue recientemente, el conductor de este autobús disminuyó la velocidad para que los pasajeros pudieran reunirse en la próxima parada. Si ese autobús partió hace mucho tiempo, el conductor aceleró para que otros autobuses no lo adelantaran. Tal sistema maximiza las ganancias de los conductores. Lo que le dio a Sheba una idea.

"Pensamos que estábamos observando una situación que recordaba los sistemas cuánticos caóticos", explicó el coautor de Sheba, Milan Krbálek.

Después de varios intentos fallidos de comunicarse con los "espías", Sheba le pidió a su estudiante que le explicara que no era del impuesto ni de la mafia. Es solo un científico loco que cambia el tequila a sus datos. Y la gente le dio sus notas. Cuando los investigadores trazaron miles de horarios de salida de autobuses, se confirmaron sus sospechas. La interacción entre los conductores condujo a la distribución de brechas entre los desechos de transporte, lo que coincidió con la estructura de algunos experimentos en física cuántica.

"Estaba pensando que algo así podría aparecer, pero me sorprendió ver una coincidencia tan exacta", dijo Sheba.

Las partículas subatómicas tienen poco en común con un sistema de bus descentralizado. Pero a lo largo de los años desde el descubrimiento de extrañas interacciones cuánticas, las mismas estructuras de datos han aparecido en otras situaciones no relacionadas. Los científicos creen que este fenómeno común, conocido como "universalidad", se debe a la conexión matemática de los fenómenos y les ayuda a simular sistemas complejos, desde Internet hasta el clima del planeta.


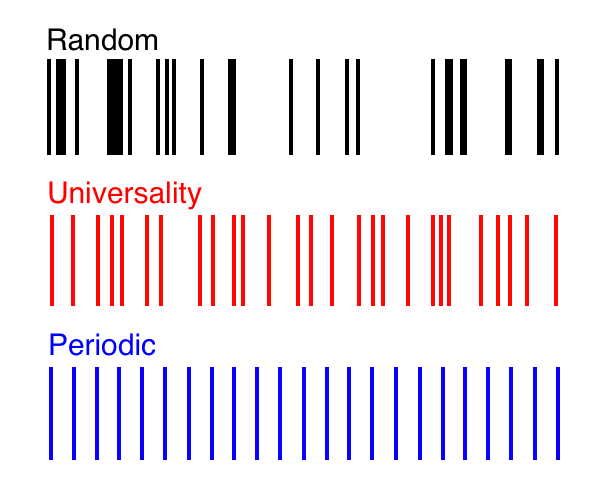El gráfico rojo representa el equilibrio perfecto entre aleatoriedad y periodicidad, conocido como universalidad. Se observa en los espectros de muchos sistemas complejos con correlación. En este espectro, la función de correlación matemática proporciona la probabilidad exacta de la presencia de dos líneas a una distancia determinada entre sí.

Dicha estructura se encontró por primera vez en la naturaleza en la década de 1950 enespectro de energía de un núcleo de uranio , un monstruo con cientos de partes móviles, oscilando y estirándose en un número infinito de formas, y emitiendo una secuencia infinita de niveles de energía. En 1972, Hugh Montgomery, especialista en teoría de números, lo observó en los ceros de la función zeta de Riemann , un objeto matemático relacionado con la distribución de números primos. En 2000, Krbalek y Sheba la encontraron en un horario de salida de autobús en Cuernavaca . Y recientemente, apareció en las mediciones espectrales de materiales compuestos, como el hielo marino y el tejido óseo humano, y en la dinámica de las señales del modelo Erd -s-Reni , una versión simplificada de Internet.

Cada uno de estos sistemas tiene un espectro: una secuencia de código de barras que representa datos tales como niveles de energía, ceros zeta, horarios de salida de autobuses o velocidades de señal. Estructuras idénticas aparecen en todo el espectro. La distribución de los datos parece aleatoria, pero al mismo tiempo, las líneas adyacentes se "repelen" entre sí, lo que conduce a una cierta regularidad de las brechas. El equilibrio exacto entre el caos y el orden, determinado por la fórmula, también aparece en problemas puramente matemáticos: determina la distancia entre los valores propios de una matriz llena de números aleatorios.

"Por qué tantos sistemas físicos se comportan como matrices aleatorias sigue siendo un misterio", dice Horng Tzer Yao, matemático de la Universidad de Harvard. "Pero en los últimos tres años, hemos dado un paso muy importante para entender esto".

Para estudiar el fenómeno de la universalidad en matrices aleatorias, los científicos comprenden un poco por qué aparece en todas partes y cómo se puede usar. En una pila de documentos nuevos, Yao y otros matemáticos describieron muchos tipos nuevos de matrices aleatorias que obedecen a varias distribuciones numéricas y reglas de simetría. Por ejemplo, los números para columnas y filas de matrices pueden tomarse de la curva de distribución normal de valores posibles, o puede rellenarlo con los valores 1 y -1. Las partes superior derecha e inferior izquierda de la matriz pueden reflejarse entre sí o no visualizarse. E independientemente de sus características, las matrices aleatorias exhiben los mismos espectros caóticos pero regulares en la distribución de sus valores propios. Por lo tanto, los matemáticos llamaron a este fenómeno "universalidad".

"Parece una ley de la naturaleza", dijo Wang Wu, matemático de la Universidad de Yale, quien, junto con Terence Tao de la Universidad de California en Los Ángeles, demostró la universalidad de una amplia clase de matrices aleatorias.

Se cree que la universalidad aparece en sistemas muy complejos, que consta de muchas partes que interactúan estrechamente entre sí para crear un espectro. Una configuración aparece en el espectro de una matriz aleatoria, por ejemplo, porque todos los elementos de la matriz se utilizan para calcular este espectro. Pero las matrices aleatorias, según Wu, son simplemente "sistemas de juguete", son lo suficientemente simples para aprender y lo suficientemente ricos como para modelar sistemas reales. La versatilidad es mucho más común. La hipótesis de Wigner (llamada así por Eugene Wigner, la síntesis que descubrió la universalidad en el espectro de los átomos), sugiere que todos los sistemas complejos con correlación son universales, desde la red cristalina hasta Internet.

Cuanto más complejo es el sistema, más universal se manifiesta, dice Laszlo Erdös de la Universidad de Munich, uno de los colegas de trabajo de Yao. "Usted cree que la universalidad es un comportamiento típico".

En muchos sistemas simples, los componentes individuales pueden influir demasiado en el resultado general, lo que cambia la apariencia del espectro. Los sistemas más grandes no tienen dominio de un solo componente. "Resulta que hay una sala con mucha gente que decide hacer algo, y la identidad de uno de ellos no es tan importante", dice Wu.


Los matemáticos usan matrices aleatorias para estudiar y predecir algunas propiedades de Internet, por ejemplo, el tamaño de un grupo de computadoras típico

Cuando un sistema demuestra universalidad, esto sirve como garantía de que es complejo y que hay suficiente correlación dentro de él para ser interpretado como una matriz aleatoria. "Eso significa que puede usar una matriz aleatoria para modelarla", dice Wu. "Puede calcular otros parámetros del modelo en función de la matriz y utilizarlos para predecir el comportamiento de este sistema".

Esta técnica permite a los científicos comprender la estructura y evolución de Internet. Algunas propiedades de esta enorme red de computadoras, como el tamaño típico de un grupo de computadoras, pueden estimarse con bastante precisión a través de las propiedades medidas de la matriz aleatoria correspondiente. "Las personas están interesadas en los clústeres y su ubicación, y esto a menudo se debe a objetivos prácticos, como la publicidad", dice Wu.

Tecnologías similares pueden conducir a mejoras en los modelos de cambio climático. Los científicos han descubierto que la presencia de universalidad, similar al espectro de energía, en el material indica una fuerte conexión de sus partes y, como resultado, una buena conductividad de líquidos, electricidad o calor. Y viceversa, la falta de versatilidad puede indicar escasez del material y sus propiedades aislantes. En un nuevo artículo presentado en una conferencia matemática en San Diego, Ken Golden, un matemático de la Universidad de Utah, y su alumno, Ben Murphy, utilizaron esta diferencia para predecir la conductividad térmica y los flujos de fluidos en el hielo marino, tanto a nivel microscópico como Ajenjo ártico, presente en territorios que se extienden por miles de kilómetros.

Una medición espectral del mosaico de ajenjo fundido fotografiado desde un helicóptero, o los datos de hielo marino obtenidos de una muestra, muestran el estado de cada uno de estos sistemas. "El flujo de fluido a través del hielo marino impulsa procesos muy importantes que deben entenderse para comprender el sistema climático", dice Golden. "Las transiciones en las estadísticas de nuestras propias decisiones representan un nuevo enfoque matemáticamente riguroso para la inclusión del hielo marino en los modelos climáticos".

El mismo truco puede conducir a una prueba simple de osteoporosis. Golden, Murphy y sus colegas descubrieron que el espectro de un hueso denso y sano tiene versatilidad, mientras que el espectro de un hueso poroso no.


Los ajenjos árticos son universales si están suficientemente conectados

"Trabajamos con sistemas cuyas" partículas "pueden tener un tamaño de milímetro o kilómetro, dice Murphy sobre los componentes del sistema. "Es sorprendente que la misma matemática los describa a todos".

La razón por la cual los sistemas reales exhiben un comportamiento similar a una matriz aleatoria es quizás más fácil de entender en el caso de un núcleo de átomo pesado. Todos los sistemas cuánticos, incluidos los átomos, funcionan de acuerdo con las reglas de las matemáticas, especialmente con la participación de matrices. "Esta es la esencia de la mecánica cuántica", dice Freeman Dyson, un ex físico matemático que ayudó a desarrollar la teoría de matrices aleatorias en los años 1960 y 1970 en el Instituto Princeton de Ingeniería Avanzada. "Cada sistema cuántico se describe mediante una matriz que representa su energía total, y las soluciones propias de la matriz son los niveles de energía del sistema cuántico".

Las matrices de átomos simples, hidrógeno y helio, se pueden calcular con precisión, y las soluciones propias obtenidas coinciden con una precisión sorprendente con los niveles de energía medidos de los átomos. Pero las matrices de sistemas más complejos, como el núcleo de uranio, se vuelven demasiado "espinosas" para "agarrarlas". Según Dyson, debido a esto, tales núcleos se pueden comparar con una matriz aleatoria. Muchas interacciones dentro del uranio, elementos de una matriz desconocida, son tan complejas que su mezcla produce ruido, como muchos sonidos superpuestos. Como resultado, la matriz desconocida que controla el núcleo se comporta como una matriz con números aleatorios, y su espectro es universal.


Tal ajenjo no conectado no tiene universalidad, su espectro es aleatorio

Los científicos aún no han desarrollado una comprensión intuitiva de por qué los sistemas complejos demuestran esta, y no otra secuencia aleatoria / periódica. "Solo sabemos esto por los cálculos", dice Wu. Otro misterio es su conexión con la función zeta de Riemann, en la que la universalidad se manifiesta en el espectro de ceros. Estos ceros están estrechamente relacionados con la distribución de números primos, los enteros irreducibles que forman el resto. Los matemáticos han estado buscando durante mucho tiempo una descripción de la distribución de números primos en una recta numérica del 1 al infinito, y la universalidad les da la clave. Algunos creen que una función zeta de Riemann puede estar matriculada lo suficientemente compleja y coherente para poseer universalidad. El descubrimiento de tal matriz tendría una "fuerte influencia" en la comprensión de la distribución de números primos, como dijo Paul Bourgade, un matemático de Harvard.

Es posible que la explicación esté oculta aún más profundamente. "Puede resultar que la matriz de la universalidad de Wigner y la función zeta no es una matriz, sino una estructura matemática que aún no se ha descubierto", dice Erdös. "Las matrices de Wigner y las funciones zeta pueden ser diferentes representaciones de esta estructura".

Muchos matemáticos están buscando una respuesta sin la garantía de una. “Nadie imaginó que los autobuses en Cuernavac serían un ejemplo de ello. Nadie imaginó que los ceros de la función zeta serían otro ejemplo, dice Dyson. "La belleza de la ciencia es su imprevisibilidad, por lo que todo lo útil proviene de las sorpresas".

Source: https://habr.com/ru/post/es399535/