Especialistas en TI caminan por caminos sin pavimentar
Después de décadas de estancamiento, se han encontrado nuevos atajos para el problema del vendedor ambulante.
 No hace mucho, un equipo de investigadores de la Universidad de Stanford y McGill rompió el récord de 35 años en ciencias de la computación en una cantidad inimaginablemente pequeña, en cuatro centésimas de un billonésimo billonésimo trillón. El avance, un problema de vendedor hecho en el problema de los clásicos de la informática, fue demasiado pequeño para cualquier valor práctico, pero dio nueva vida en busca de soluciones aproximadas mejoradas.La tarea se forma de la siguiente manera: para un conjunto de ciudades conectadas por carreteras, es necesario encontrar la forma más corta de visitar cada ciudad con un retorno al punto de partida. Las soluciones al problema tienen aplicaciones prácticas, desde perforar agujeros en placas de circuitos impresos hasta administrar el cronograma de tareas en una computadora y organizar las propiedades del genoma.El problema del vendedor es fácil de formular y, en teoría, fácil de resolver al verificar todos los caminos cerrados posibles para encontrar el más corto. El problema con el enfoque de la fuerza bruta es que cuando crece el número de ciudades, el número correspondiente de caminos comienza a exceder rápidamente las capacidades de las computadoras más rápidas. Para diez ciudades, hay más de 300,000 rutas. Para 15 ciudades, su número aumenta a 87 mil millones.
No hace mucho, un equipo de investigadores de la Universidad de Stanford y McGill rompió el récord de 35 años en ciencias de la computación en una cantidad inimaginablemente pequeña, en cuatro centésimas de un billonésimo billonésimo trillón. El avance, un problema de vendedor hecho en el problema de los clásicos de la informática, fue demasiado pequeño para cualquier valor práctico, pero dio nueva vida en busca de soluciones aproximadas mejoradas.La tarea se forma de la siguiente manera: para un conjunto de ciudades conectadas por carreteras, es necesario encontrar la forma más corta de visitar cada ciudad con un retorno al punto de partida. Las soluciones al problema tienen aplicaciones prácticas, desde perforar agujeros en placas de circuitos impresos hasta administrar el cronograma de tareas en una computadora y organizar las propiedades del genoma.El problema del vendedor es fácil de formular y, en teoría, fácil de resolver al verificar todos los caminos cerrados posibles para encontrar el más corto. El problema con el enfoque de la fuerza bruta es que cuando crece el número de ciudades, el número correspondiente de caminos comienza a exceder rápidamente las capacidades de las computadoras más rápidas. Para diez ciudades, hay más de 300,000 rutas. Para 15 ciudades, su número aumenta a 87 mil millones.Algoritmo de Christofides
En la era de la informática, los matemáticos esperaban que alguien encontrara un enfoque conveniente para el problema: un algoritmo que permita resolverlo en un tiempo razonable. Pero aunque los programadores avanzaron en casos específicos, determinando el camino más corto para 49 ciudades en la década de 1950, para 2,392 ciudades en la década de 1980 y para 85,900 ciudades en 2006, nadie propuso un algoritmo que resuelva el problema de manera efectiva en el caso general. Según el notable trabajo de 1972, es posible que dicho algoritmo no exista en absoluto. El informático Richard Karp, de la Universidad de California en Berkeley, demostró que el problema del vendedor es NP-completo, lo que significa que no hay un algoritmo eficiente (a menos que alguien demuestre que P = NP, pero la mayoría de los científicos creen que esto no es así) .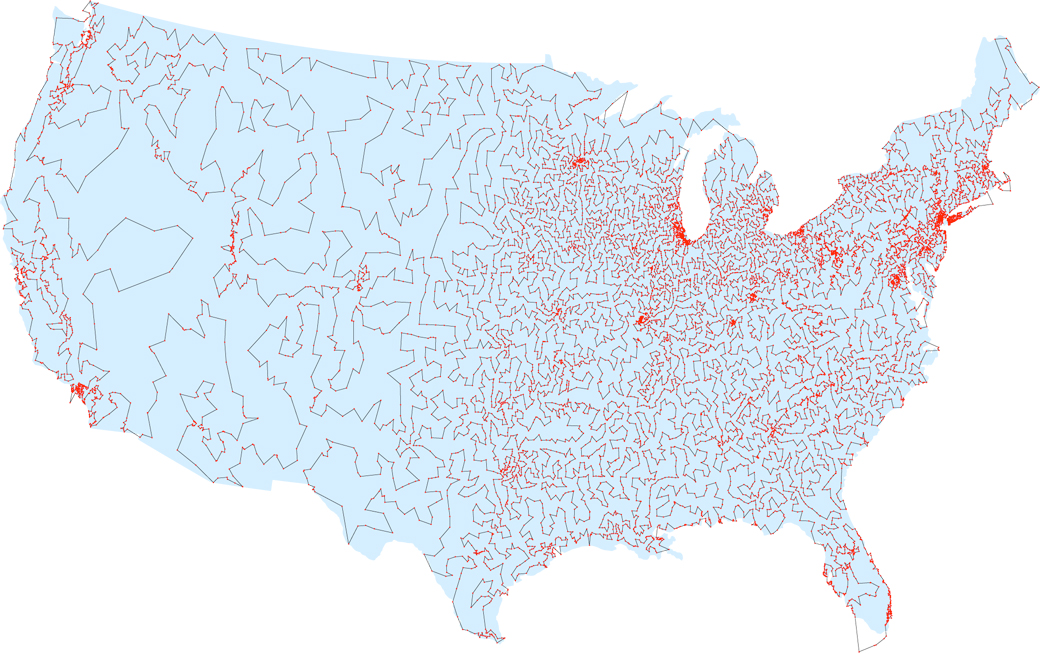 La ruta más corta a través de las 13,509 ciudades en los Estados Unidos con una población de más de 500 (según datos de 1998)Después de la publicación de Karp, muchos científicos informáticos comenzaron a desarrollar un algoritmo efectivo para encontrar soluciones aproximadas al problema: caminos cerrados cuya longitud es solo un poco más larga que la más corta. Y aquí fueron más afortunados: en 1976, Nikos Christofides, profesor del Imperial College de Londres, desarrolló un algoritmo que produce caminos que se garantiza que no superarán el camino más corto en más del 50%.Después de su creación, muchos científicos decidieron que este algoritmo, que es lo suficientemente simple para que los estudiantes estudien en una hora, se convertirá en un enlace intermedio, después de lo cual se encontrará una solución verdadera más compleja y mejor aproximada. Pero décadas después, tales algoritmos nunca aparecieron."Casi todos los estudiantes de ciencias de la computación pasaron semanas o meses tratando de mejorar el algoritmo de Christofides", dijo Sanjeev Arora, científico de la Universidad de Princeton.Finalmente, en 2011, el equipo de Stanford y McGill superó la garantía del 50% para ciertos tipos de tareas de vendedor y demostró que sus soluciones superarían el camino más corto en no más del 49.99999999999999999999999999999999999999999999999696%.Desde entonces, han aparecido varios algoritmos aproximados mejorados, gracias a una nueva mirada al problema. Aunque estas aproximaciones se aplican solo a ciertos tipos de tareas de vendedor ambulante, su enfoque es bastante prometedor, según Michael Gomans, un especialista en TI del Instituto de Tecnología de Massachusetts."Solo tocamos la superficie ligeramente", dice. "Creo que tal vez en cinco años, lograremos resultados más impresionantes".
La ruta más corta a través de las 13,509 ciudades en los Estados Unidos con una población de más de 500 (según datos de 1998)Después de la publicación de Karp, muchos científicos informáticos comenzaron a desarrollar un algoritmo efectivo para encontrar soluciones aproximadas al problema: caminos cerrados cuya longitud es solo un poco más larga que la más corta. Y aquí fueron más afortunados: en 1976, Nikos Christofides, profesor del Imperial College de Londres, desarrolló un algoritmo que produce caminos que se garantiza que no superarán el camino más corto en más del 50%.Después de su creación, muchos científicos decidieron que este algoritmo, que es lo suficientemente simple para que los estudiantes estudien en una hora, se convertirá en un enlace intermedio, después de lo cual se encontrará una solución verdadera más compleja y mejor aproximada. Pero décadas después, tales algoritmos nunca aparecieron."Casi todos los estudiantes de ciencias de la computación pasaron semanas o meses tratando de mejorar el algoritmo de Christofides", dijo Sanjeev Arora, científico de la Universidad de Princeton.Finalmente, en 2011, el equipo de Stanford y McGill superó la garantía del 50% para ciertos tipos de tareas de vendedor y demostró que sus soluciones superarían el camino más corto en no más del 49.99999999999999999999999999999999999999999999999696%.Desde entonces, han aparecido varios algoritmos aproximados mejorados, gracias a una nueva mirada al problema. Aunque estas aproximaciones se aplican solo a ciertos tipos de tareas de vendedor ambulante, su enfoque es bastante prometedor, según Michael Gomans, un especialista en TI del Instituto de Tecnología de Massachusetts."Solo tocamos la superficie ligeramente", dice. "Creo que tal vez en cinco años, lograremos resultados más impresionantes".Árbol más corto
 Mona Lisa como un camino entre 100,000 ciudadesEl algoritmo de Christofides no comienza con la búsqueda del camino más corto, sino con la búsqueda de un árbol de expansión mínimo: un conjunto de ramas que conectan ciudades sin bucles cerrados. A diferencia del camino más corto, el árbol de expansión mínimo es bastante fácil de construir: debe comenzar buscando el camino más corto entre las dos ciudades; Esta será la primera rama. Para agregar lo siguiente, debe encontrar el camino más corto entre la nueva ciudad y una de las dos anteriores, y así sucesivamente, hasta que todas las ciudades estén cubiertas.El árbol resultante no es una de las posibles soluciones al problema del vendedor ambulante, ya que no nos da un camino cerrado. Pero se puede convertir en ese camino, imaginando que las ramas son paredes, y luego caminando a lo largo del árbol para que su dedo toque la pared hasta llegar al principio. La caminata resultante pasa por cada ciudad y regresa, pero generalmente está lejos del camino más corto, ya que pasa muchas veces a lo largo de los mismos segmentos: caminamos cada pared en un árbol dos veces, una a cada lado.Pero la ruta resultante en el peor de los casos no es más larga que la ruta más corta dos veces. Al agregar ramas especialmente seleccionadas y aplicar algunos trucos, Christofides mostró cómo cortar este camino para que no supere el más corto en más del 50%.Un árbol de expansión mínimo es un punto de partida natural para construir una solución temporal corta. Pero este enfoque también sirvió como punto de partida para los investigadores que intentan exprimir una garantía del 50% de Christofides. Después de todo, aunque un árbol de expansión mínimo al principio parece efectivo, otros árboles pueden ser más adecuados para el proceso de convertir árboles en una solución alternativa; por ejemplo, solo necesita agregar una pata a un árbol sin ramificación, para que se convierta en una solución alternativa.Entonces, el objetivo era encontrar un árbol que lograra un equilibrio entre la longitud y la conversión simple a una solución alternativa. No existen algoritmos efectivos para buscar un árbol ideal (si P = NP no es cierto), pero un algoritmo aproximado exitoso solo necesita encontrar lo suficientemente bueno.
Mona Lisa como un camino entre 100,000 ciudadesEl algoritmo de Christofides no comienza con la búsqueda del camino más corto, sino con la búsqueda de un árbol de expansión mínimo: un conjunto de ramas que conectan ciudades sin bucles cerrados. A diferencia del camino más corto, el árbol de expansión mínimo es bastante fácil de construir: debe comenzar buscando el camino más corto entre las dos ciudades; Esta será la primera rama. Para agregar lo siguiente, debe encontrar el camino más corto entre la nueva ciudad y una de las dos anteriores, y así sucesivamente, hasta que todas las ciudades estén cubiertas.El árbol resultante no es una de las posibles soluciones al problema del vendedor ambulante, ya que no nos da un camino cerrado. Pero se puede convertir en ese camino, imaginando que las ramas son paredes, y luego caminando a lo largo del árbol para que su dedo toque la pared hasta llegar al principio. La caminata resultante pasa por cada ciudad y regresa, pero generalmente está lejos del camino más corto, ya que pasa muchas veces a lo largo de los mismos segmentos: caminamos cada pared en un árbol dos veces, una a cada lado.Pero la ruta resultante en el peor de los casos no es más larga que la ruta más corta dos veces. Al agregar ramas especialmente seleccionadas y aplicar algunos trucos, Christofides mostró cómo cortar este camino para que no supere el más corto en más del 50%.Un árbol de expansión mínimo es un punto de partida natural para construir una solución temporal corta. Pero este enfoque también sirvió como punto de partida para los investigadores que intentan exprimir una garantía del 50% de Christofides. Después de todo, aunque un árbol de expansión mínimo al principio parece efectivo, otros árboles pueden ser más adecuados para el proceso de convertir árboles en una solución alternativa; por ejemplo, solo necesita agregar una pata a un árbol sin ramificación, para que se convierta en una solución alternativa.Entonces, el objetivo era encontrar un árbol que lograra un equilibrio entre la longitud y la conversión simple a una solución alternativa. No existen algoritmos efectivos para buscar un árbol ideal (si P = NP no es cierto), pero un algoritmo aproximado exitoso solo necesita encontrar lo suficientemente bueno.Viaje fraccional
El camino hacia un árbol "razonablemente bueno" incluía una técnica popular, aunque contraintuitiva, que reconocía soluciones fraccionadas para tareas específicas. Por ejemplo, una solución alternativa puede incluir viajar a medio camino entre Minneapolis y Detroit, y a medio camino entre Cleveland y Detroit. Desde un punto de vista práctico, ese camino no tiene sentido. Pero puede describirse matemáticamente con precisión y, a diferencia del clásico problema del vendedor ambulante, una versión fraccionada de este tipo puede resolverse de manera eficiente.Muchos problemas de aproximación en ciencias de la computación pueden resolverse calculando soluciones para la versión fraccional del problema y luego redondeando inteligentemente los recursos compartidos para obtener una solución aproximada al problema original. Pero hasta hace poco, nadie había descubierto cómo hacerlo en el caso del problema del vendedor ambulante.En 2009, Amin Saberi de la Universidad de Stanford y Arash Asadpour, entonces estudiante de posgrado, desarrollaron un esquema de redondeo general que usa números aleatorios para seleccionar una solución entera que conserva tantas propiedades de la solución fraccional como sea posible. Saberi creía que este patrón recordaba a un "martillo pesado en busca de un clavo". Y sospechaba que la tarea del vendedor podría ser el clavo correcto.Unos meses más tarde, Saber, Asadpur, Gomans, Shayan Gharan, estudiante graduado de Stanford y Aleksander Madry, que ahora trabajan en la Escuela Politécnica Federal de Lausana en Suiza, mostraron que la nueva técnica de redondeo puede proporcionar un buen algoritmo aproximado para una de las opciones tareas del vendedor, el caso "asimétrico". Un año después, Saberi, Garan y Mohit Singh, de la Universidad McGill, utilizaron el mismo enfoque para desarrollar un nuevo algoritmo aproximado para el problema habitual del vendedor ambulante. El mayor problema del vendedor ambulante solicitado fue el camino entre 85.900 ciudades, calculado en 2006. La ubicación de las "ciudades" corresponde al diseño de un chip de computadora específico creado en el laboratorio de Bell, y la solución es el camino más corto para el corte con láser.Habiendo recibido un mapa de ciudades y rutas, el nuevo algoritmo comienza calculando la solución fraccional exacta del problema del vendedor ambulante. Luego redondea esta solución a un árbol de expansión, que en teoría debería acercarse a un equilibrio entre la longitud y la conversión simple a una solución alternativa. Finalmente, el algoritmo incluye este árbol, y no el árbol de expansión mínimo, en la red de Christofides.El nuevo algoritmo fue "una idea que podríamos explicar en un par de horas, pero su prueba tomó alrededor de un año", dice Saberi.Después de un largo análisis, el equipo de Stanford / McGill pudo mejorar el algoritmo de Christofides en una pequeña fracción para una amplia subclase de tareas de vendedor, "gráfico". Unos meses después, otros equipos, inspirados por el éxito, utilizaron otros esquemas de redondeo para obtener algoritmos para el caso gráfico con mejores aproximaciones. El récord actual es del 40%, que es mucho mejor que el 50% de Christofides.El caso gráfico "incluye muchas de las mismas dificultades que se encuentran en el problema general", dice Arora, y agrega que los esquemas que funcionan en el caso gráfico pueden ser útiles para el problema general del vendedor ambulante.No obstante, dice Saber, es probable que resolver el problema general del vendedor aproximado requiera nuevas ideas. “Un descubrimiento matemático es como moverse en una habitación oscura. Extiende la mano y busca una silla, busca una mesa ”, dice, parafraseando al matemático Andrew Wiles. “En algún momento, la mano encuentra un interruptor, y de repente todo se aclara. En el caso de la tarea del vendedor, incluso después de tantos trabajos que han encontrado tantos límites de lo posible, no me parece que ya hayamos encontrado este cambio ".
El mayor problema del vendedor ambulante solicitado fue el camino entre 85.900 ciudades, calculado en 2006. La ubicación de las "ciudades" corresponde al diseño de un chip de computadora específico creado en el laboratorio de Bell, y la solución es el camino más corto para el corte con láser.Habiendo recibido un mapa de ciudades y rutas, el nuevo algoritmo comienza calculando la solución fraccional exacta del problema del vendedor ambulante. Luego redondea esta solución a un árbol de expansión, que en teoría debería acercarse a un equilibrio entre la longitud y la conversión simple a una solución alternativa. Finalmente, el algoritmo incluye este árbol, y no el árbol de expansión mínimo, en la red de Christofides.El nuevo algoritmo fue "una idea que podríamos explicar en un par de horas, pero su prueba tomó alrededor de un año", dice Saberi.Después de un largo análisis, el equipo de Stanford / McGill pudo mejorar el algoritmo de Christofides en una pequeña fracción para una amplia subclase de tareas de vendedor, "gráfico". Unos meses después, otros equipos, inspirados por el éxito, utilizaron otros esquemas de redondeo para obtener algoritmos para el caso gráfico con mejores aproximaciones. El récord actual es del 40%, que es mucho mejor que el 50% de Christofides.El caso gráfico "incluye muchas de las mismas dificultades que se encuentran en el problema general", dice Arora, y agrega que los esquemas que funcionan en el caso gráfico pueden ser útiles para el problema general del vendedor ambulante.No obstante, dice Saber, es probable que resolver el problema general del vendedor aproximado requiera nuevas ideas. “Un descubrimiento matemático es como moverse en una habitación oscura. Extiende la mano y busca una silla, busca una mesa ”, dice, parafraseando al matemático Andrew Wiles. “En algún momento, la mano encuentra un interruptor, y de repente todo se aclara. En el caso de la tarea del vendedor, incluso después de tantos trabajos que han encontrado tantos límites de lo posible, no me parece que ya hayamos encontrado este cambio ".Source: https://habr.com/ru/post/es399873/
All Articles