No mentiré, tengo muchas ganas de ver la película Spider-Man: Homecoming [Spider-Man: Homecoming]. Mientras tanto, la única salida para mí será hacer la física de Spider-Man. Y me ocuparé de sus nuevas alas de tela de araña que se ven en el último avance.Para los fanáticos, noto que algunos de los cómics originales sobre Spider-Man realmente mostraron cómo los usa, aunque no siempre los usó para volar.Planificación física
¿Qué sucede después de que Spider-Man salta de un edificio? Puedo simular su movimiento al aceptar que tres fuerzas actúan sobre él: gravedad, resistencia al aire y elevación. Con su permiso, describiré cada uno de ellos.• Gravedad: una fuerza constante hacia abajo proporcional a la masa de la emergencia (al menos en la superficie de la Tierra).• Resistencia. Imagine que está tirando un objeto a través de un mar gigante de pelotas de ping pong. Reemplace las bolas con aire, y será casi lo mismo. La resistencia aumenta con la velocidad.• Fuerza de elevación. De nuevo, imagine colisiones con bolas, pero después de las cuales las bolas rebotan. Reemplazando las bolas con aire, recibirás un levantamiento dependiendo del ángulo de ataque, superficie y velocidad.Aquí hay un hermoso diagrama de las fuerzas de una persona que planea en las alas de una emergencia. Sí, mientras lo modelamos con un triángulo.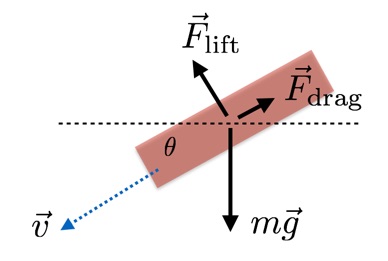 En nuestro modelo simple, la fuerza de elevación es perpendicular a la velocidad, y la resistencia se dirige en la dirección opuesta. Para simular el movimiento de una emergencia con alas, necesito una fórmula para ambos.
En nuestro modelo simple, la fuerza de elevación es perpendicular a la velocidad, y la resistencia se dirige en la dirección opuesta. Para simular el movimiento de una emergencia con alas, necesito una fórmula para ambos.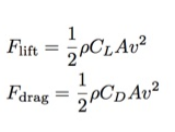 Estos son valores de fuerzas que son importantes para nosotros. Son similares, con la excepción de C L (coeficiente de elevación) y C D (coeficiente de arrastre). En ambos casos, ρ es la densidad del aire (1.2 kg / m 3 ), y v es la velocidad.¿Qué es la A? Esta es el área transversal de una persona (emergencia en nuestro caso). En teoría, A para resistencia y fuerza de elevación debería diferir, dependiendo del ángulo de ataque. Pero no siempre sé exactamente lo que estoy haciendo, es por eso que verifiqué con diferentes fuentes, y el artículo de 2011 " La trayectoria de un Batman cayendo"de la revista física Journal of Physics Special Topics. En ella, los autores usaron la misma área para resistencia y levantamiento, así que haré lo mismo.
Estos son valores de fuerzas que son importantes para nosotros. Son similares, con la excepción de C L (coeficiente de elevación) y C D (coeficiente de arrastre). En ambos casos, ρ es la densidad del aire (1.2 kg / m 3 ), y v es la velocidad.¿Qué es la A? Esta es el área transversal de una persona (emergencia en nuestro caso). En teoría, A para resistencia y fuerza de elevación debería diferir, dependiendo del ángulo de ataque. Pero no siempre sé exactamente lo que estoy haciendo, es por eso que verifiqué con diferentes fuentes, y el artículo de 2011 " La trayectoria de un Batman cayendo"de la revista física Journal of Physics Special Topics. En ella, los autores usaron la misma área para resistencia y levantamiento, así que haré lo mismo.Modelado de trayectoria
Si una emergencia salta de un edificio, ¿hasta dónde puede moverse en una caída? ¿Qué diferencia le darán las alas de araña? Modelar el estado de emergencia no es tan simple, ya que la resistencia y la elevación dependen de la velocidad. Dicha trayectoria solo se puede calcular utilizando un modelo numérico en el que el movimiento se divide en pequeños pasos.Hagamos la aproximación. Primero, calculamos el área de superficie de la emergencia. Aproximadamente estimando, obtuve: lo que nos da un área de aproximadamente 0,651 m 2 con alas y 0,513 m 2 sin ellas. Otros valores:• Coeficiente de elevación = 1.45 (el valor se toma del trabajo en Batman)• Coeficiente de resistencia = 0.4 (desde el mismo lugar)• Peso = 64 kg• Velocidad inicial = 8 m / s (horizontal)• Y otra suposición: un ángulo de ataque constante, en relación con el cual los coeficientes de arrastre y elevación no cambian.Sin dudarlo, salté al mundo de los modelos numéricos. Dejé comentarios en el código para que puedas rehacerlo para usarlo como tarea.
lo que nos da un área de aproximadamente 0,651 m 2 con alas y 0,513 m 2 sin ellas. Otros valores:• Coeficiente de elevación = 1.45 (el valor se toma del trabajo en Batman)• Coeficiente de resistencia = 0.4 (desde el mismo lugar)• Peso = 64 kg• Velocidad inicial = 8 m / s (horizontal)• Y otra suposición: un ángulo de ataque constante, en relación con el cual los coeficientes de arrastre y elevación no cambian.Sin dudarlo, salté al mundo de los modelos numéricos. Dejé comentarios en el código para que puedas rehacerlo para usarlo como tarea.GlowScript 2.1 VPython
A1=0.651
A2=0.513
g=vector(0,-9.8,0)
m=64
CL=1.45
CD=0.4
rho=1.2
v0=8
p=vector(v0,0,0)*m
p2=p
t=0
dt=0.01
h=40
r=vector(0,h,0)
r2=r
f1=series(color=color.red)
f2=series(color=color.blue)
while r.y>0:
v=p/m
v2=p2/m
Fd=-.5*rho*A1*CD*(mag(v)**2)*norm(v)
Fd2=-.5*rho*A2*CD*(mag(v2)**2)*norm(v2)
FL=-.5*rho*A1*CL*(mag(v)**2)*cross(norm(v),vector(0,0,1))
FL2=-.5*rho*A2*CL*(mag(v2)**2)*cross(norm(v2),vector(0,0,1))
F=m*g+Fd+FL
F2=m*g+Fd2+FL2
p=p+F*dt
p2=p2+F2*dt
r=r+p*dt/m
r2=r2+p2*dt/m
t=t+dt
f1.plot(r.x,r.y)
f2.plot(r2.x,r2.y)
print("Glide Ratio 1 = ",-p.x/p.y)
print("Glide Ratio 2 = ", -p2.x/p2.y)
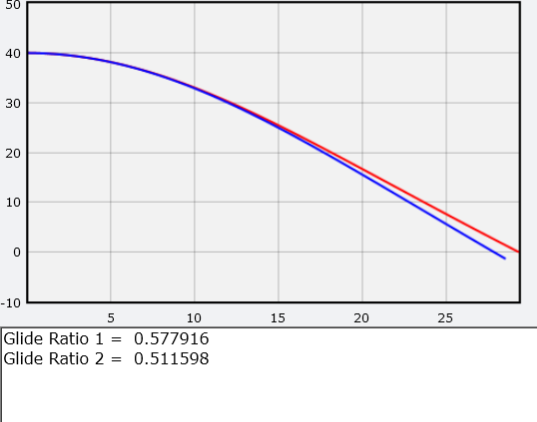 En mi modelo, la línea roja representa la trayectoria de la emergencia con alas y la línea azul sin alas. También obtengo el valor de la calidad aerodinámica. Como al final se mueve a una velocidad constante, esta relación será simplemente la relación de la componente x del momento dividido por la componente y.TareaUse este modelo numérico para responder las siguientes preguntas . No te preocupes, no romperás nada. Si haces algo con el código, simplemente reinicia y comienza de nuevo.• Según Wikipedia, para un paracaidista que salta con un traje alado, la calidad aerodinámica (la relación de elevación a arrastre) tiene un valor del orden de 2.5: 1 (es decir, nuestro programa deduciría el número 2.5). ¿Puedes corregir el código para que el programa produzca ese valor? Sugerencia: cambie tanto el área de superficie como la velocidad inicial.• ¿Qué pasa si una emergencia cae verticalmente? ¿Qué velocidad máxima ganará con las alas y sin ellas?• ¿Qué tan rápido necesita moverse la emergencia horizontalmente para que vuele en lugar de bajar al comienzo del vuelo?• ¿Puede un salto de emergencia, apuntando hacia abajo, para ganar más velocidad y durante algún tiempo ir en vuelo horizontal?• ¿Puedes construir un modelo mejorado que tenga en cuenta el ángulo de ataque? Quizás puedas, pero me parece que volar a baja velocidad es un tema bastante complicado.
En mi modelo, la línea roja representa la trayectoria de la emergencia con alas y la línea azul sin alas. También obtengo el valor de la calidad aerodinámica. Como al final se mueve a una velocidad constante, esta relación será simplemente la relación de la componente x del momento dividido por la componente y.TareaUse este modelo numérico para responder las siguientes preguntas . No te preocupes, no romperás nada. Si haces algo con el código, simplemente reinicia y comienza de nuevo.• Según Wikipedia, para un paracaidista que salta con un traje alado, la calidad aerodinámica (la relación de elevación a arrastre) tiene un valor del orden de 2.5: 1 (es decir, nuestro programa deduciría el número 2.5). ¿Puedes corregir el código para que el programa produzca ese valor? Sugerencia: cambie tanto el área de superficie como la velocidad inicial.• ¿Qué pasa si una emergencia cae verticalmente? ¿Qué velocidad máxima ganará con las alas y sin ellas?• ¿Qué tan rápido necesita moverse la emergencia horizontalmente para que vuele en lugar de bajar al comienzo del vuelo?• ¿Puede un salto de emergencia, apuntando hacia abajo, para ganar más velocidad y durante algún tiempo ir en vuelo horizontal?• ¿Puedes construir un modelo mejorado que tenga en cuenta el ángulo de ataque? Quizás puedas, pero me parece que volar a baja velocidad es un tema bastante complicado.