Si volvemos a la historia del estudio de las rutas de vuelo desde la Tierra hasta la Luna, entonces debe retroceder hace un siglo y medio, en 1865, cuando se publicó la nueva novela de Jules Verne "De la Tierra a la Luna de manera directa en 97 horas y 20 minutos". Por supuesto, esto estaba lejos del primer libro que describía tal vuelo, pero fue la primera novela en la que el autor decidió abordar la descripción del viaje desde un punto de vista científico.Además, el nivel de preparación de este texto se entiende especialmente bien ahora, ya que por primera vez el viaje espacial no solo se mostró, sino que todos los matices, a veces muy pequeños, se analizaron en detalle. Ahora les gusta criticar la novela por esos errores que cometió el autor. Pero con tal volumen de trabajo, ¡sería sorprendente si no hubiera ningún error! Y ahora no son sus errores lo que lo sorprenden más, sino sobre lo que tenía razón. Por ejemplo, la idea de sistemas de purificación de oxígeno tanto en la carcasa de Columbiada como en la nave espacial Soyuz es muy similar. Solo Julio Verne tenía hidróxido de sodio, y ahora se usa hidróxido de litio.
Aún más interesantes son los momentos en que tenía razón, a pesar de las suposiciones incorrectas. Por ejemplo, Perelman lo criticó por dar datos erróneos sobre el tiempo de vuelo de la Tierra a la Luna e incluso los hizo en nombre de la novela. El matemático realizó cálculos más precisos por el método especificado, habiendo recibido una cifra del orden de seis días, dos días más que en la novela. Y sus cálculos, dentro del marco de este método, eran de hecho correctos. Es realmente posible volar a la Luna solo en cuatro días (en realidad, muchos dispositivos llegaron a la Luna aproximadamente en este tiempo), pero en seis días ya es imposible. ¡El método de cálculo fue elegido incorrectamente por el escritor de ciencia ficción, y la cifra resultó ser correcta!Aún así, por ejemplo, poco después del lanzamiento de la novela "Alrededor de la Luna", muchos dudaron de la posibilidad de tal trayectoria de un sobrevuelo cercano de la Luna bajo la influencia de solo fuerzas gravitacionales. Solo a principios del siglo XX, al evaluar las órbitas en los sistemas estelares binarios, se mostró realmente la posibilidad de la existencia de tales órbitas. Esto es lo que escribió la revista inglesa "Knowledge" a principios del siglo XX en el artículo "Astronomía de Julio Verne":«, . , . . , . , , . , , , . . . . , . , , , ».En otras palabras, las tareas que Jules Verne intentó resolver en ese momento no solo estaban a la vanguardia de la ciencia: a menudo planteaban preguntas que la ciencia no podía responder.Sin embargo, uno no debe olvidar que no hizo todo esto solo. Al escribir todos sus libros, el autor intentó recurrir a especialistas en cualquier campo. Según sus diarios, los cálculos para el vuelo de la Tierra a la Luna fueron realizados por su primo Henri Garce (1815-1871), un profesor de matemáticas en el Liceo de Napoleón (ahora el Liceo de Enrique IV). Por cierto, aquí puedes ver su libro en francés, dedicado a la cosmografía de Leçons nouvelles de Cosmographie (1854). Y sus cálculos fueron bastante precisos. Por ejemplo, aquí, de acuerdo con los datos del libro, calculé la fecha exacta de inicio de la tripulación de Columbiada.
Henri Garcet (1815-1871)Sin embargo, probablemente no hubiéramos sabido acerca de sus cálculos si Jules Verne no los hubiera colocado al comienzo del libro "Alrededor de la Luna", usándolos en la conversación de la tripulación del caparazón Columbiada. Escriben que los lectores del periódico "Debates" de fecha 7 de noviembre de 1869 estaban literalmente asombrados al ver cálculos matemáticos complejos: la publicación de la novela comenzó en este periódico.Así es como se describió el modelo matemático del vuelo a través de los labios de Michel Ardan y Barbicane:"¿Sabes, Barbicane, en qué he estado pensando toda la noche?"
- ¿Qué tal? El presidente preguntó.
— . , , , . : , , , .
— , — , — , , , , , .
— , , — .- - ?
— .
— ?
…
"Sí, querido amigo". Habiendo tenido en cuenta todas las condiciones conocidas del problema: la
distancia desde el centro de la tierra hasta el centro de la luna, el radio de la tierra, la masa de la tierra, la masa de la luna, puedo determinar con precisión la velocidad inicial de nuestro proyectil y con la fórmula más simple.
- ¿Cuál es la fórmula?
- Pero ya ves. Pero solo no tacharé la curva descrita por nuestro caparazón entre la Luna y la Tierra, dado su movimiento relativo alrededor del Sol. Supongamos que ambos planetas están inmóviles. Eso será suficiente.
- por qué?
- Debido a que así es como se resuelven las tareas llamadas "tareas de tres cuerpos", el método integral para resolver tales problemas aún no se ha desarrollado lo suficiente.Después de un tiempo, también se introdujo la fórmula, que se presentó a los lectores:donde r es el radio de la Tierra, es la distancia entre los centros de la Tierra y la Luna, x es la distancia del núcleo desde la Tierra. V 0 es la velocidad inicial del núcleo. V es la velocidad a una distancia de x.Y el vuelo se veía asíAquí me gustaría señalar que esta fórmula con los datos iniciales indicados es realmente cierta. Y realmente muestra con precisión el efecto gravitacional de la Tierra y la Luna en el dispositivo en cualquier momento dado. Es bastante fácil derivar de la ley de conservación de la energía.Derivación de la fórmula Verne-Garce.
mv2 / 2 – γMm/R – γMm/R =const
m M,M – , ,
γ – , R - , R-
. .
mv2 / 2 – γMm/x– γMm/(D-x) =mv02 / 2 – γMm/r – γMm/(d-r)
m,
v2 / 2 –v02 / 2=γM/x+ γM/(D-x)– γM/r – γM/(d-r)
1/2*(v2-v02 )=γM(1/-1/r+M/M*1/(d-x)-M/M*1/(d-r))
1/2*(v2-v02 )=γM/r(r/-1+M/M(r/(d-x)-r/(d-r))
mg=mγM/r2 γM=g*r2
1/2*(v2-v02 )=gr(r/-1+M/M(r/(d-x)-r/(d-r))
Entonces, ¿cuál es el trato? El problema es que no tiene en cuenta la dinámica del sistema. La luna gira alrededor de la Tierra a una velocidad de aproximadamente 1 km / s. Este es precisamente el problema de este problema. Como resultado, cuando se intenta volar de acuerdo con el esquema anterior, cuando la estación vuela a un punto neutral entre la Tierra y la Luna, el campo de la Luna no lo capturará en absoluto, ya que este último volará lejos del proyectil a una velocidad de un kilómetro por segundo, y el proyectil comenzará a caer a la Tierra. Pero entonces había esperanza de que la captura del dispositivo por la Luna ocurriera, y un esquema similar, en una primera aproximación, muestra con precisión la dinámica del vuelo. Con la mano ligera de Julio Verne, un método similar para calcular el vuelo pronto se hizo muy popular. Comenzó a usarse no solo en libros de arte, sino también en trabajos científicos serios.Cabe señalar que los astrónomos entendieron la importancia de tener en cuenta la dinámica. Sí, y las ecuaciones diferenciales que tienen en cuenta tanto la gravedad como la dinámica, podrían componerse fácilmente. Simplemente tampoco podría encontrar una solución simple. En realidad, como ahora se entiende bien, el problema de los tres cuerpos no tiene una solución analítica general. El problema podría resolverse solo numéricamente, lo que significaba un número muy, muy grande de cálculos de rutina, que podrían pasar meses o incluso años de vida. En el momento de la publicación de la novela, un problema similar se resolvió numéricamente solo dos veces. Además, el primer intento fue más de cien años antes de la publicación de la novela, en 1759.Se sabe que Edmund Halley, compilando un catálogo de cometas, notó que varios cometas que aparecieron en el cielo en diferentes momentos tienen parámetros muy similares. Habiéndolos verificado, decidió que podría ser el mismo cometa. Entonces ella será llamada por su nombre. El cometa Halley apareció en el cielo en 1531, 1607 y 1682. Es decir, el período de circulación fue de 75-76 años, y el científico predijo la próxima aparición para 1758. Y todo sería maravilloso, si no fuera por un "pero": en el tiempo estimado, el cometa en el cielo nunca apareció.Entonces el matemático francés Cleo decidió calcular su trayectoria con la mayor precisión posible. Incluyendo, teniendo en cuenta las perturbaciones de su trayectoria debido al atractivo de Júpiter y Saturno. Fue un trabajo muy agotador y largo, aunque no lo hizo solo: fue asistido por el astrónomo J. Lalande y la matemática Madame Lepot. Resultó que la diferencia con las estimaciones previas del período de revolución del cometa es de 618 días, y llegará a su perihelio el 13 de abril de 1759. Con un posible error por un mes. La evaluación resultó ser muy precisa: el cometa pasó su perihelio el 12 de marzo. Fue una victoria para los matemáticos y una muy buena confirmación de las leyes de Newton.Sobre este cálculo, Laland más tarde escribió: "Calculamos seis meses desde la mañana hasta la noche, a veces sin siquiera levantar la vista de la comida, y la consecuencia de esto fue que alteré mi salud por el resto de los días de mi vida. La ayuda de Madame Lepot fue tal que sin ella nunca nos atreveríamos a emprender este enorme trabajo, que consistía en calcular la distancia del cometa desde dos planetas, Júpiter y Saturno, para cada grado de la esfera celeste durante 150 años ".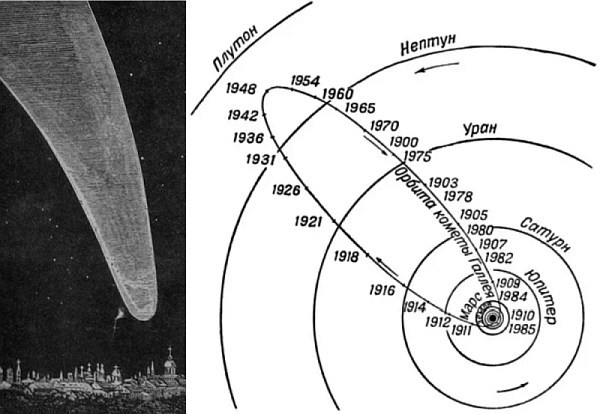
Puedes ver la trayectoria del cometa Halley en relación con las órbitas de planetas Lasegunda vez que se usó un método similar en 1829, nuevamente al calcular la trayectoria del cometa Halley. Las estimaciones dieron la fecha del regreso del cometa al Sol el 15 de noviembre de 1835. El cometa regresó el 16 de noviembre, solo un día tarde.Como resultado, un método numérico similar ha demostrado su precisión. Pero de la historia anterior, puede ver claramente cuánto trabajo tedioso se requería. ¡Seis meses de trabajo de tres matemáticos tardaron en calcular solo una trayectoria con parámetros iniciales bien conocidos! Pero para calcular las trayectorias de un vuelo de la Tierra a la Luna, fue necesario evaluar docenas, si no cientos de trayectorias, con diferentes parámetros iniciales. De lo contrario, es imposible obtener, por ejemplo, la velocidad exacta, la fecha de lanzamiento, las características de la trayectoria, los posibles errores, los parámetros de vuelo de la estación cerca de la luna, etc. Esto podría llevar años de vida. Es decir, esta solución se consideró muy difícil. Especialmente para una tarea que no tiene mucho significado práctico.Al mismo tiempo, también había confianza en que podría encontrarse una solución analítica al problema de los tres cuerpos. Al menos permitiendo, en una primera aproximación, evaluar los parámetros de vuelo.Y el método propuesto por Julio Verne parecía dar una respuesta a esta pregunta. Después de todo, matemáticamente, en el marco de los supuestos iniciales, era impecable. Sí, no tuvo en cuenta la dinámica, pero muchos esperaban que esta suposición fuera normal, y la trayectoria real del proyectil de la Tierra a la Luna se vería así.Cálculo del libro "Naves espaciales. (Comunicaciones interplanetarias en las fantasías de los novelistas) ”1928Y la belleza matemática, junto con la gran popularidad de la novela, jugó una broma cruel: utilizando este método, prácticamente todos los pioneros de la exploración espacial - Goddard , Sternfeld , Obert , Max Valle y muchos otros - evaluaron el vuelo . A veces, extremadamente raramente, también estimaron no un vuelo directo, sino por la elipse del satélite de la Tierra. Pero este método también tuvo sus inconvenientes. Por ejemplo, por alguna razón, muchos estaban seguros de que alcanzar la luna era suficiente para caer en su esfera de acción; Además, dicen, la atracción de la luna debería hacer el resto. Aunque, como se dijo anteriormente, la posibilidad de volar en el problema de los tres cuerpos ya ha sido probada.Una buena ilustración sería el artículo de Werner von Braun en el diario semanal del 18 de octubre de 1952, en el que von Braun describió cómo, en su opinión, sería una expedición a la luna.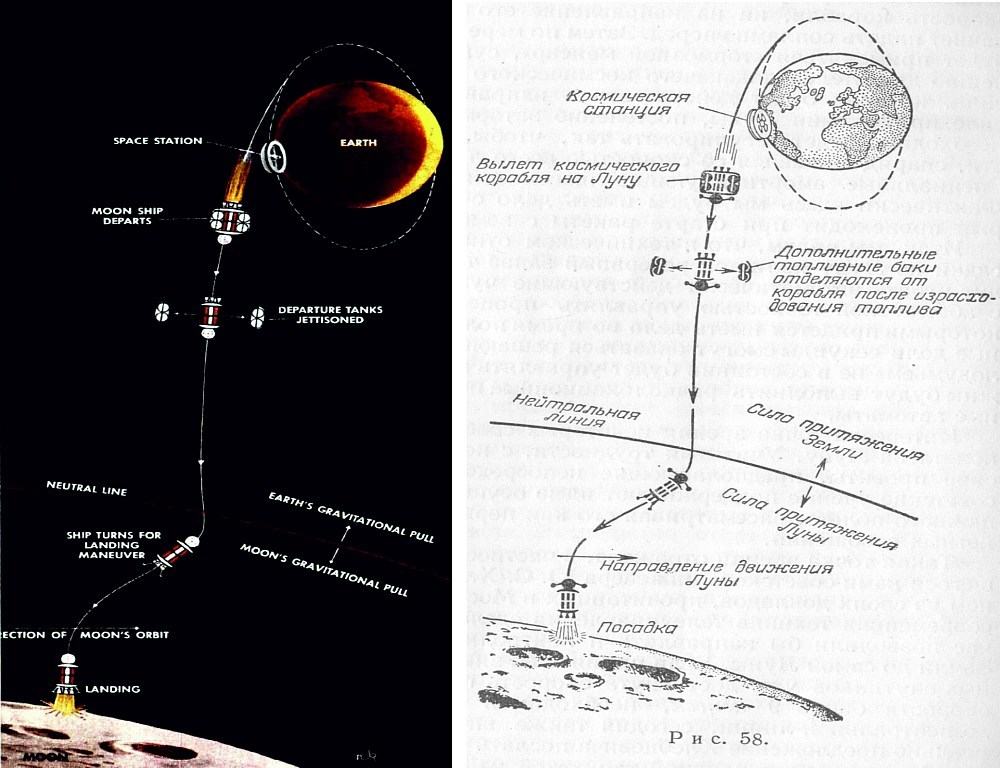
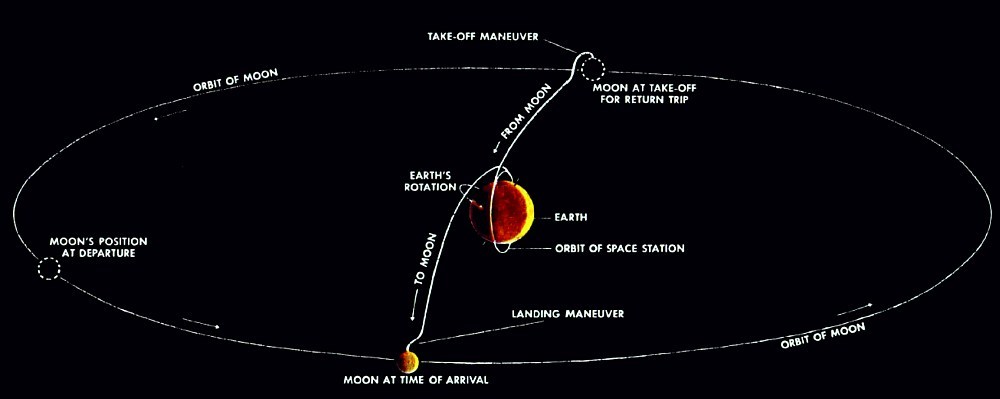El artículo en sí se puede descargar aquí.De la ilustración es claramente visible que es precisamente el esquema de Julio Verne el que se presenta allí: primero, alcanzar una región neutral entre la Tierra y la Luna, y luego caer sobre la Luna bajo la influencia de su atracción. El cañón ha sido reemplazado por un cohete, pero el principio básico no ha cambiado. Aunque han pasado casi cien años desde la publicación de la novela.Pero pronto la aproximación a los vuelos desde la Tierra a la Luna comenzó a cambiar. Incluyendo, gracias al desarrollo de computadoras electrónicas.Continuación sigue .