Cómo hacer fondos de pantalla imposibles: una historia de simetrías prohibidas

A la izquierda hay un patrón de papel tapiz con simetría de rotación de sexto orden alrededor de cada una de las rosetas de color verde marrón. A la derecha hay un patrón de papel tapiz con simetría de espejo en relación con las líneas horizontales que pasan a través de cada elemento elíptico de un adorno de vitral.

A primera vista, inventar un fondo de pantalla no es más difícil que completar tareas de un jardín de infantes. Los diseñadores pueden elegir cualquier combinación de colores y formas para la pieza original, y simplemente multiplicarla en dos direcciones. Dependiendo del patrón de la pieza inicial y la elección de las direcciones, pueden aparecer simetrías adicionales, por ejemplo, simetría de sexto orden en la primera imagen o simetría de espejo en la segunda. Ambos patrones fueron creados por el matemático Frank Farris de la Universidad de California, Santa Clara.


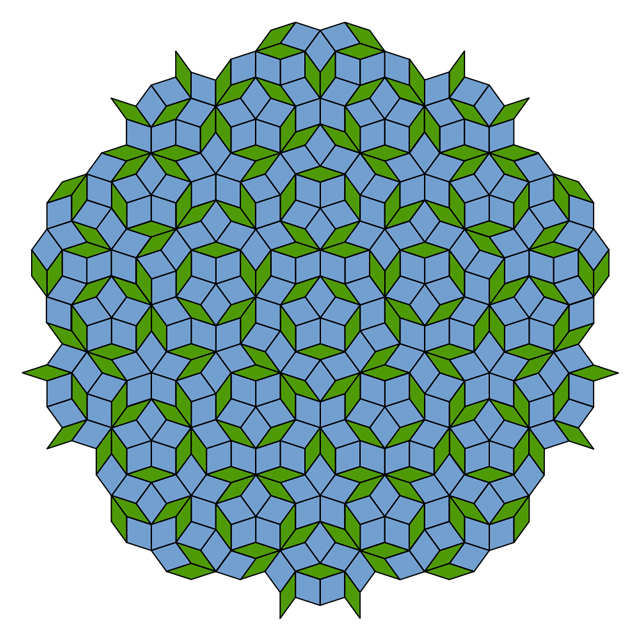Los mosaicos de Penrose muestran muchos ejemplos de simetría local de quinto orden, pero no tienen repeticiones del patrón. Cuando se llenan áreas grandes en el plano, la proporción del número de baldosas anchas al número de angostas se aproxima a la proporción dorada.

Pero, aunque es posible hacer fondos de pantalla con simetrías rotacionales de segundo, tercer, cuarto o sexto orden, es imposible crear fondos de pantalla con simetría de quinto orden [el orden muestra cuántas veces el patrón se autoalineará durante una rotación de 360 ​​° - aprox. transl.]. Los matemáticos conocen esta restricción desde hace casi 200 años como una "restricción cristalográfica". La geometría del pentágono prohíbe los patrones con simetría de quinto orden. Lo mismo es cierto para pedidos de siete o más.

Sin embargo, los patrones más interesantes, como los mosaicos de Penrose, muestran simetría local de quinto orden en muchos lugares y en diferentes escalas, solo sin patrones repetitivos. Utilizando un método diferente del enfoque de Penrose, Farris frenó la inusual geometría de simetría de quinto orden y creó un nuevo conjunto de imágenes emocionantes: pseudopapeles que no parecen obedecer, a primera vista, la restricción cristalográfica.


Fig. 4 La

cuarta figura parece un contraejemplo para la restricción cristalográfica, que posee simetría rotacional de quinto orden alrededor del punto A, mientras que el patrón puede desplazarse en un plano en las direcciones AB o AC. De hecho, Faris escribe en su artículo para la revista Notices of the American Mathematical Society que esta imagen es simplemente una falsa inteligente.

"Sabes que la simetría que observas es imposible", dice Stephen Kennedy del Carleton College en Minnesota.

La simetría rotacional de quinto orden alrededor del punto A parece cumplirse. Pero si observa detenidamente, notará que las ruedas alrededor de los puntos B y C son ligeramente diferentes de A. Si pudiéramos alejarnos del patrón para ver más repeticiones, entonces las repeticiones visibles del patrón serían cada vez menos como un patrón en la región del punto. E, incluso si copias más convincentes de A aparecieran en otros lugares, como en la Fig. 5. Faris demostró que tales ilusiones también se pueden crear a mayor escala, alejándose del patrón y repitiéndolo un cierto número de veces, específicamente, el número de veces correspondiente a los números de la serie de Fibonacci (1, 1, 2, 3, 5, 8, 13, 21, ... donde cada número siguiente es la suma de los dos anteriores), que también juega un papel en la geometría de las fichas de Penrose.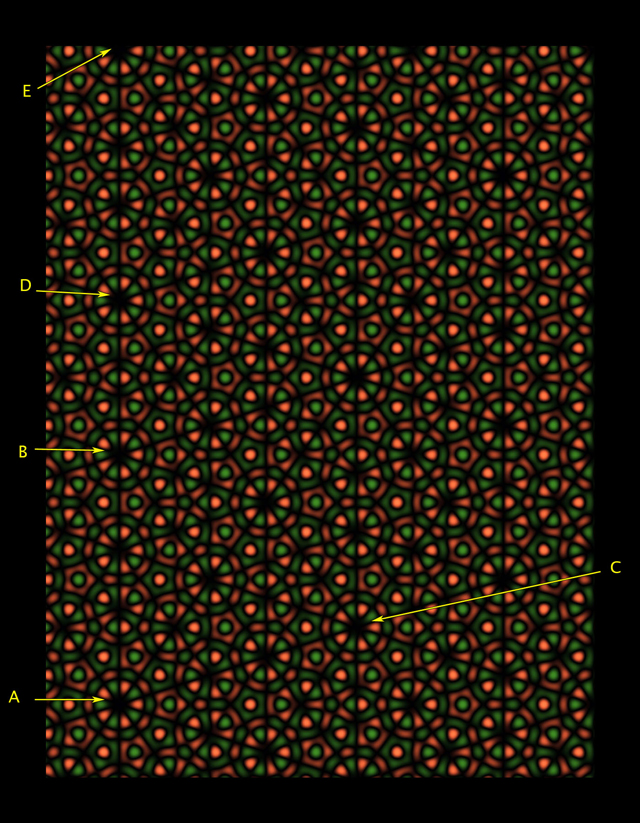


Fig. 5 5

"Por razones, entendemos que esto es una especie de engaño", dice Faris. Sin embargo, como él escribe en el artículo, estas imágenes "invitan a nuestros ojos a estudiarlas y disfrutar de repeticiones casi perfectas".

Faris pensó en estas falsificaciones, cambiando la tecnología con la que creó fondos de pantalla reales con simetría rotacional de tercer orden, como en la Fig. 6)

Para crear una simetría de tercer orden, Faris comenzó a trabajar en un espacio tridimensional, que tiene una rotación especialmente natural, clasificando a través de tres coordenadas espaciales y rotando puntos en el espacio 120 grados alrededor de la diagonal. Luego, Faris creó patrones de papel tapiz tridimensionales, superponiendo sinusoides especialmente seleccionados y combinándolos con una paleta de colores preseleccionada. Los puntos se tiñeron según su posición en los sinusoides superpuestos. Entonces Faris sacó un fondo de pantalla plano, limitando este color a un plano bidimensional perpendicular al eje de rotación del espacio original.

Este enfoque suave y sinusoidal para crear patrones de papel tapiz es diferente del método tradicional de copiar y pegar, dice Kennedy. "Esta es una forma muy nueva de crear patrones simétricos".


Fig. 6 6

Parece que el mismo procedimiento llevado a cabo en el espacio de cinco dimensiones debería haber llevado a la creación de un patrón con simetría de quinto orden, si tan solo no supiéramos que esto era imposible. Curiosamente, pensó Faris, ¿en qué punto falla este sistema?

Teóricamente, el espacio de cinco dimensiones es posible, aunque es difícil de imaginar. Tiene un análogo natural de la simetría de rotación del quinto orden, como en el espacio tridimensional: la simetría del tercero. En el espacio de cinco dimensiones, se puede seleccionar uno de los dos planos, cada uno de los cuales es perpendicular al eje de rotación y al otro plano. Cada uno de ellos se puede girar alrededor de un punto en 72 o 144 grados. Puede parecer difícil imaginar dos planos y una línea recta perpendicular entre sí, pero en cinco dimensiones todos tienen suficiente espacio.

Faris entendió el problema: si un plano perpendicular corta con precisión el espacio tridimensional y contiene fondos de pantalla infinitos con un número infinito de puntos con coordenadas enteras, entonces dos planos perpendiculares en el espacio de cinco dimensiones son irracionales y no contienen puntos con coordenadas enteras (excepto el punto de referencia) . Dado que el patrón de fondo de pantalla creado a partir de sinusoides se repite a través de cambios por números enteros, tales planos no heredan patrones de espacios de orden superior.

"Así es como aparece la mosca en la sopa", escribe Faris en el artículo.

Sin embargo, la ilusión de la estructura del fondo de pantalla aparece en estos dos planos, gracias a la participación de los llamados la proporción áurea, un número irracional que describe las direcciones de dos planos y los números de Fibonacci.

Gracias a sus relaciones, Faris logró demostrar que aunque no hay puntos con coordenadas enteras en dos planos, cada uno de ellos se acerca mucho a la dispersión sin fin de puntos con coordenadas enteras, cuyas coordenadas son números de Fibonacci. Cada vez que el avión se acerca a uno de estos puntos de Fibonacci, el patrón se ve casi igual que en el punto de referencia, lo que crea la ilusión de una copia exacta.



Faris también descubrió cómo combinar los colores y patrones de las fotos de la naturaleza con funciones de onda para incluirlos en el diseño de patrones, como resultado de lo cual puede obtener una gran cantidad de fondos de pantalla "falsos". En la figura anterior, puede ver las ramas de los árboles que migraron de la fotografía.

Source: https://habr.com/ru/post/es400591/