Tautologías importantes en la ciencia. Parte 1. Física

¿Sabes qué es una tautología lógica? Probablemente lo sepas. Y en caso de que no lo sepas, el autor intentará explicar este concepto ahora. No comenzaremos a cambiar al lenguaje seco y formal de las matemáticas, no seremos pedantes sin alma como Wikipedia, y diremos en sentido figurado: una tautología es una especie de Ouroboros que se muerde la cola. Por ejemplo, "nada es cuando no hay nada", o "los objetos que son lo suficientemente estrechos y bajos como para atravesar esta puerta pasarán fácilmente por ella" y similares. Tales declaraciones son siempre verdaderas y, en términos generales, no llevan ninguna información nueva. Sorprendentemente, una serie de importantes leyes y principios de la ciencia contienen tautologías ocultas, que, sin embargo, no restan importancia y corrección. Interesante? ¡Entonces adelante, debajo del corte!

El emperador Sarlac Grant Scenticus III estaba aburrido. Muy aburrido Por lo general, cuando sentía aburrimiento, jugaba piedras (un juego bastante simple pero complicado, similar al mismo tiempo que nuestras fichas, reversi y Go ). Sin embargo, hoy ninguno de los filósofos que solían jugar con él vino. Se sentó mirando y miró una de las posiciones.

El experimentador interno de Grant decidió contar el número de posiciones posibles. Dejémoslo en este lugar y hagamos nuestro propio recuento.

De acuerdo con las reglas, se permite tener hasta 3 piedras en una celda. Hay 6 piedras en total (3 para cada jugador). No consideraremos el número de todas las posiciones posibles. Es mucho más interesante calcular cuántas formas puede diseñar una posición. Pero primero, mira el dibujo.

Por simplicidad, estamos considerando solo una celda. La posición anterior se puede obtener, por ejemplo, de tres maneras diferentes en las que colocamos las piedras en el tablero: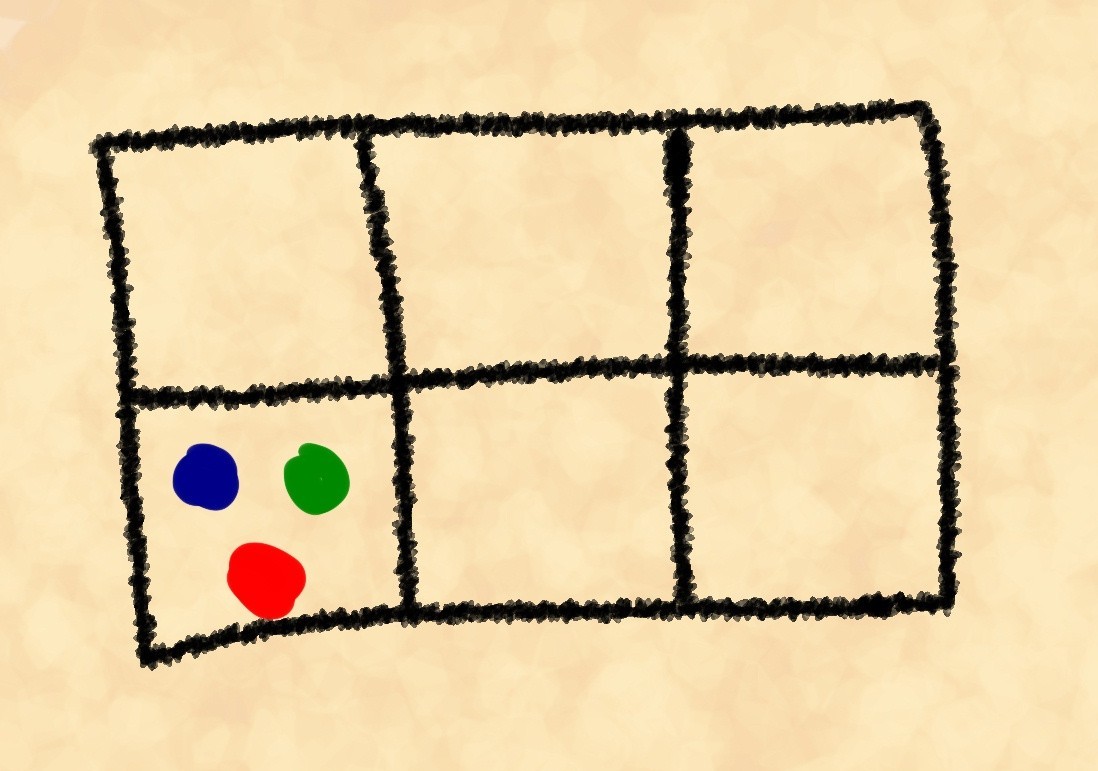

  

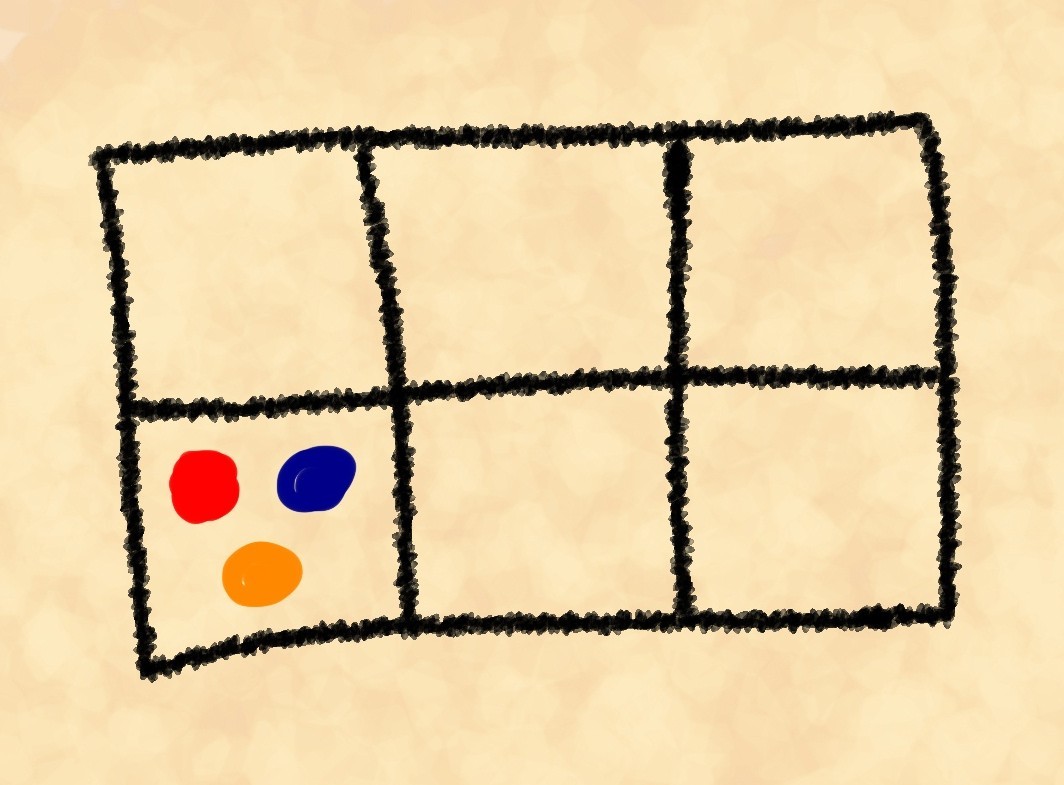pintamos las piedras condicionalmente para poder distinguirlas unas de otras. Obviamente, hay muchos más de tres métodos. ¿Pero cuánto exactamente? La primera de las tres piedras podemos elegir de seis maneras. Cada una de estas seis opciones continúa con una elección de la segunda piedra de las cinco restantes, y la última de las cuatro restantes. Tenemos$$ , sin embargo, al mismo tiempo, permitimos repeticiones, por ejemplo, rojo-azul-amarillo, amarillo-rojo-azul y azul-rojo-amarillo son el mismo "cálculo". Para encontrar el número de repeticiones, descubrimos de cuántas maneras podemos colocar tres piedras del mismo color en el tablero. La primera puede ser cualquiera de las tres piedras necesarias, la segunda debe ser una de las dos restantes, la tercera será la última piedra que necesitamos:$6\cdot5\cdot4=120$

$$. Como resultado, tenemos 120/6 = 20 formas de colocar las piedras de la manera requerida. Llamemos a este número el peso de esta posición. Por supuesto, no tiene nada que ver con el peso físico, solo este nombre es generalmente aceptado en las estadísticas. Vamos a complicar la tarea. Calculemos los pesos de estas posiciones: si es demasiado vago para comprender todas estas matemáticas, omita el siguiente párrafo. Primera posición:$3\cdot2\cdot1=6$




  

1. Difundimos 2 piedras en una de las dos celdas izquierdas: $$$2\cdot6\cdot5/2=30$
2. En la segunda celda colocamos dos piedras de las 4 restantes: $$$4\cdot3/2=6$
3. Total tenemos $$$30\cdot6/2=90$.

$$$30\cdot4\cdot3/2=180$$$. La división en todos los casos se realiza para deshacerse de las repeticiones.$4\cdot6\cdot3\cdot5\cdot2\cdot4\cdot3/24=360$

Entonces, tenemos los siguientes pesos: 90 para el primer diseño, 180 para el segundo y 360 para el tercero. ¿Has notado que cuanto más aerodinámica es la posición, menor es su peso? Su Majestad Grant se dio cuenta de esto. Y ahora va a calcular el peso de las posiciones de juego reales.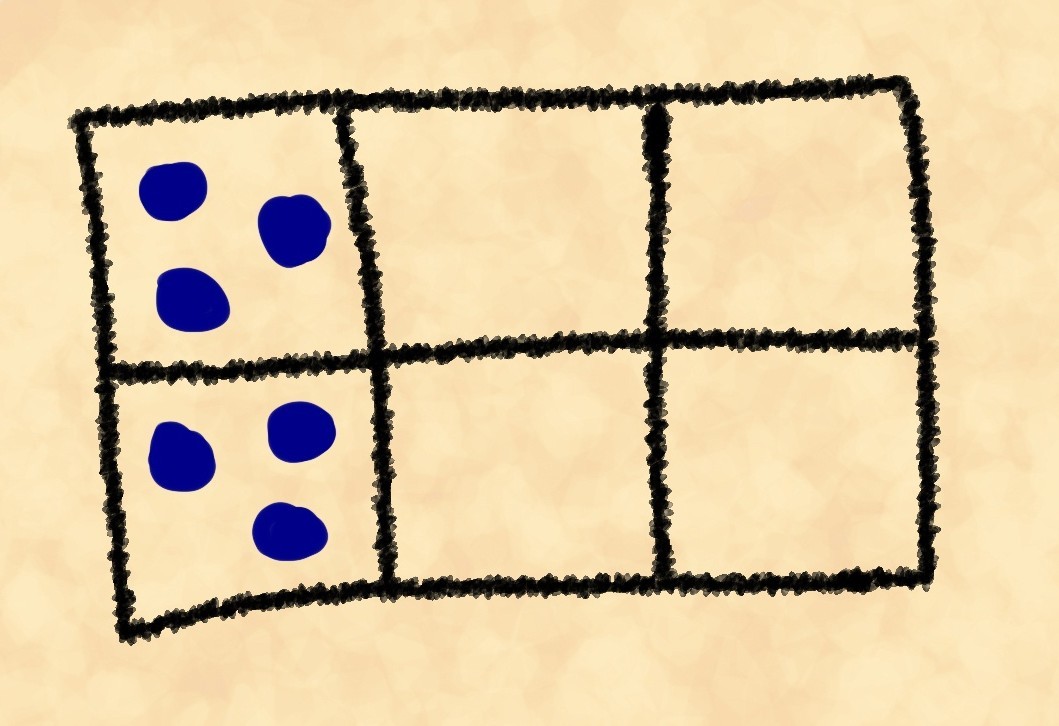

  

Resulta, respectivamente, 90, 360 y 720. Sin embargo, aquí termina su paciencia (como, probablemente, la suya). Empuja el tablero molesto, esparciendo las piedras al azar, y nota al filósofo Klofzus parado en la puerta.

"Dime, filósofo", pregunta con una nota de descontento, "¿por qué, cuando empujo el tablero, las piedras vuelan alrededor al azar, de manera uniforme, y no caben tres en una jaula desde el borde?

Klofzius, en respuesta a esto, sonrió y dijo:

"Observé sus cálculos durante algún tiempo, señor supremo, y probablemente ya podría responder esta pregunta usted mismo". Pero aún diré: se pueden pedir piedras desde el borde del tablero de noventa maneras diferentes, y setecientas veinte se pueden dispersar por todas las celdas. Para las piedras, hay muchas más formas de esparcirse por el tablero de manera uniforme que recogidas en el borde.

Quizás aquí dejemos Sarlak. Pero preste atención a la explicación de Klofzus: las piedras se dispersan en el tablero porque hay muchas más formas de dispersarse de manera uniforme que de forma ordenada. Y la diferencia entre el número de métodos (los pesos de los diseños de las piedras) cuanto mayor, mayor es el tablero y el número de piedras. Para un tablero de 15 celdas (3 por 5) y 15 piedras, el peso de un diseño completamente ordenado (3 piedras por celda a lo largo de un borde) es de aproximadamente 1.4 millones (1,401,400 si es exactamente) y para un uniforme (uno en cada celda) - aproximadamente 1.3 billones , es decir, casi un millón de veces más. Por lo tanto, en este caso es mucho más fácil obtener un desorden que obtener un pedido. Uno involuntariamente recuerda una declaración tan maravillosa: "Los huevos se rompen a cada paso, pero nadie ha visto nunca,para que los fragmentos de un huevo roto se unan y se conviertan en un huevo entero. Y todo porque solo hay una forma de obtener un huevo entero e infinitamente muchas formas de romperse ".

Para resumir la regularidad que notamos:

en cualquier proceso que ocurra por sí solo, sin influencia externa adicional, es muy probable que se logre el resultado que se puede lograr de la mayor manera posible.

Mire más de cerca, es una tautología en todo su esplendor. Para simplificar las cosas, simplemente afirmo que "lo que es más fácil de suceder sucede con más frecuencia". Sin embargo, también es una de las leyes físicas más importantes. Muchos de ustedes probablemente ya han entendido que estamos hablando de la segunda ley de la termodinámica. Veamos una de sus formulaciones "oficiales": la

entropía de un sistema cerrado no puede disminuir.

Ahora esto es menos como una tautología, ¿verdad? Pero, ¿qué tipo de palabra inteligente es entropía?

Imaginemos el aire llenando una habitación. Se compone de una gran cantidad de moléculas. Si dividimos mentalmente la habitación en celdas, obtendremos un análogo tridimensional del juego de piedras en un tablero muy grande con una gran cantidad de piedras. Cada posición del juego en este caso se denomina macroestado del sistema. Cada uno de los diseños de piedras que implementan una posición particular es un microestado . Tomamos dos números: el número de todos los microestados que realizan este macroestado y el número de todos los microestados posibles. Si dividimos el primero en el segundo, obtendremos la probabilidad de este macroestado.

Definición del libro: la entropía del estado de un sistema es el logaritmo de la probabilidad de este estado.

Lo traducimos a un lenguaje que Grant comprende: la entropía de una posición es el logaritmo del peso de una posición determinada. Tratemos de hacer esto aún más claro: cuantas más formas pueda obtener una posición, más entropía.

Ahora vemos que la formulación del libro del segundo principio dice lo siguiente: desde una posición en sí misma, solo puede ocurrir una transición a una posición que se puede obtener en más o con el mismo número de caminos que el inicial.

Intentemos simplificarlo: si sacudimos el tablero, antes obtendremos una posición que sea más fácil de conseguir.

Parece que hemos vuelto a la tautología. Sin embargo, incluso si se trata de una tautología, el segundo principio es una de las leyes físicas más importantes. Además, esta es la única ley de la física que nos dice que el tiempo debe fluir en cierta dirección, lo que hace la diferencia entre el pasado y el futuro.

Finalmente, veamos un par de formulaciones más del segundo comienzo:

• Postulado de Clausius: un proceso circular es imposible, cuyo único resultado es la transferencia de calor de un cuerpo menos caliente a un calentador
• Postulado de Thomson: un proceso circular es imposible, cuyo único resultado sería la producción de trabajo enfriando el depósito de calor.

Como puede ver, ya no hay una tautología. Y ninguno de ellos es obvio. Sin embargo, se puede demostrar que ambas formulaciones son completamente equivalentes a la tautológica "es muy probable que ocurra algo más probable". A veces, para aprender algo nuevo, primero tenemos que darnos cuenta de algo obvio.

En la siguiente parte, consideraremos otra "tautología científica" que, a primera vista, viola la segunda ley de la termodinámica.

Source: https://habr.com/ru/post/es400803/