Moon Duchin, Profesor Asociado de Matemáticas y Director del Programa de Ciencia, Tecnología y Sociedad de la Universidad de Tufts (EE. UU.)

Los partidos políticos y las comisiones electorales en los Estados Unidos, Rusia y otros países tradicionalmente "engañan" con el tamaño y la forma de los distritos electorales, tratando de aislar a la parte de protesta del electorado en reservas separadas o, por el contrario, difundir una pequeña mancha en los distritos electorales vecinos. Debido a tales manipulaciones, jerrymandering , los distritos a veces adquieren contornos muy extraños. Pero todo es legal. Hasta ahora, no existe una legislación normal con fórmulas matemáticas que describan la forma geométrica del distrito. El Profesor Asociado de Matemáticas en la Universidad de Tufts tiene la intención de corregir esta deficiencia y ofrece varios modelos matemáticos.

Jerrymandering se usa a menudo en países con elecciones parlamentarias mayoritarias y un sistema de partidos fuerte. Para que el número máximo de "sus propios" diputados entren al parlamento, los votantes del partido de oposición se concentran en varios distritos electorales, mientras que en el resto hacen una pequeña pero confiada ventaja para su partido. Es por eso que los distritos electorales se crean con un número desigual de votantes, así como distritos electorales de una forma territorial extraña.

Por ejemplo, en los Estados Unidos, la jerrymandering se usó para neutralizar a los votantes negros para que sus candidatos no fueran al parlamento (hubo casos de discriminación positiva cuando se promovió a los candidatos negros de esta manera). Y en Rusia en 2015, antes de las elecciones parlamentarias, se aprobó una ley sobre el corte de "distritos" de distritos , en el que pequeños sectores de grandes ciudades con electorados desleales se unen a grandes territorios rurales con una población leal. Como resultado, jerrymandering realiza la misma tarea: bloquea el paso de candidatos "maliciosos" al parlamento en la mayoría de los distritos.

Por ejemplo, en la región de Novosibirsk, las autoridades dividieron la población de la ciudad en cuatro partes y unieron cada una de ellas al territorio de la región.


Distritos electorales de la región de Novosibirsk

En los Estados Unidos, la situación con jerrymandering es aún peor, porque en la mayoría de los estados, la división de distritos es competencia de los parlamentos regionales (es decir, está en manos de un partido con una mayoría parlamentaria). Por ejemplo, la región de Novosibirsk ni siquiera se acerca en su grado de idiotez a la distribución de Maryland en ocho condados.


Segundo distrito pcs. Maryland


Tercer distrito pcs. Maryland

Además, las constituciones estatales generalmente proporcionan solo reglas básicas sobre la forma de las circunscripciones o no tienen reglas. Generalmente se indica que el distrito debe ser "compacto", pero esto es claramente una declaración amplia y subjetiva.

Para cambiar la situación, Moon Dachin estableció una organización experta de cinco miembros, el Grupo de Geometría y Gerrymandering Métrico (MGGG), que abrió una lista de correo para comenzar a discutir el problema de la jerrymandering en la comunidad científica. Describió los objetivos de la organización en una entrevista con la revista Chronicle of Higher Education.

¿Qué es la compacidad?

El profesor asociado Dachin propone considerar la posibilidad de utilizar varios conceptos para describir la forma aceptable del distrito, es decir, verificar objetivamente el requisito de "compacidad", que está escrito en las constituciones estatales.

Por ejemplo, puede considerar un parámetro como el puntaje de Polsby-Popper , que se calcula como la relación entre el área de un condado y el área de un círculo cuya longitud es igual al perímetro del condado.


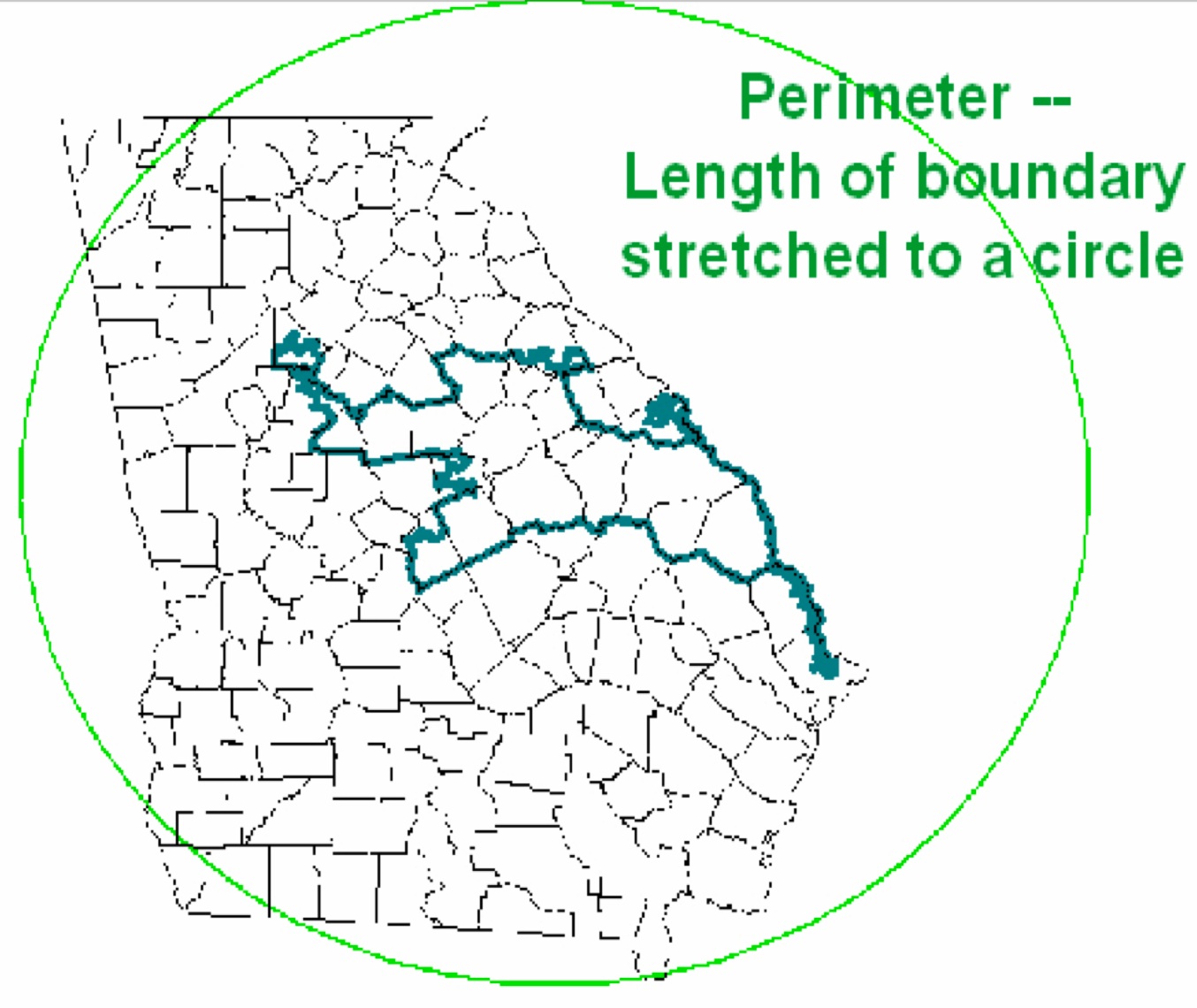Puntuación Polsby Popper

Otra opción es una relación simple del área del distrito al área del círculo en el círculo circunscrito.


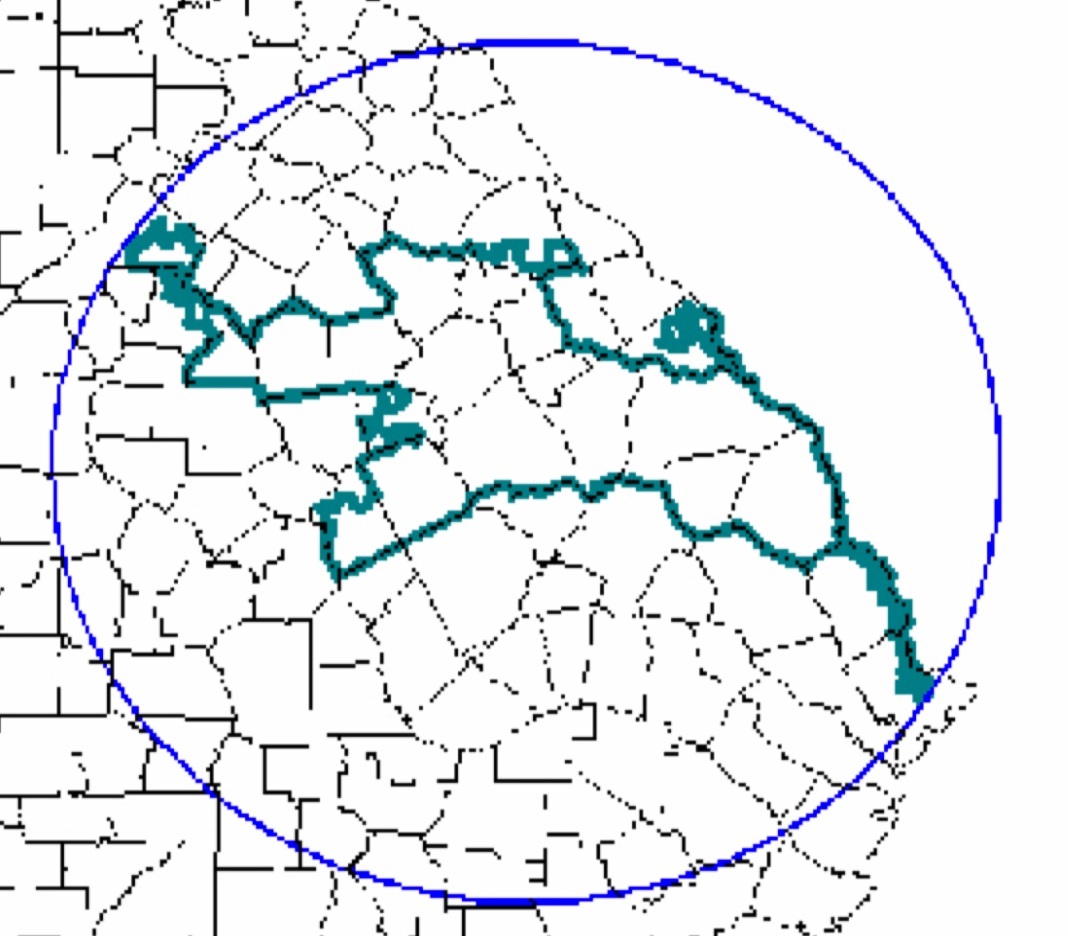La razón del área del distrito al área del círculo.

Moon Dachin dice que actualmente está trabajando en problemas de geometría métrica dentro del marco de la teoría de grupos geométricos . Este es un campo de las matemáticas que estudia grupos finitamente generados utilizando las conexiones entre sus propiedades algebraicas y las propiedades topológicas y geométricas de los espacios en los que actúan dichos grupos, o de los grupos mismos, considerados como objetos geométricos. En el sitio web personal de Danchin , puede encontrar varios trabajos científicos en esta área en los que describe un parámetro como la distancia promedio entre todos los puntos de una figura arbitraria (probablemente, el parámetro aún debe normalizarse, por ejemplo, por el diámetro del mismo círculo descrito). Este parámetro es bastante adecuado como característica de la compacidad.

Otra opción para evaluar la compacidad, que los expertos mencionan en broma , es la prueba interocular Grofman, propuesta por el científico estadounidense Bernie Grofman. Esta prueba le permite determinar visualmente el nivel de gerrymandering midiendo qué tan anchos son los ojos de una persona, quién está mirando el mapa y evaluando la escala del fraude. Por cierto, una vez se ofreció la misma prueba para evaluar el porno "hardcore". El punto es que es difícil formalizar tales cosas, pero cuando lo ves lo entiendes de inmediato (mira nuevamente los condados de Maryland).

El profesor asociado de la Universidad de Tufts confía en que con la ayuda de las matemáticas, se pueden resolver muchos problemas sociales. Pero la dificultad es que los políticos a menudo no pueden entender conceptos matemáticos simples. Por lo tanto, será bastante difícil convencerlos de que introduzcan tales fórmulas en las leyes y la Constitución del país. Después de todo, primero deben entenderse. Moon Dachin da un ejemplo del concepto de falta de eficiencia , que describe Jerrymandering con ejemplos simples, un caso único cuando un juez de EE. UU. Entendió las matemáticas y dijo que "le gustaba". Este documento matemático formó la base del Whitford v. Nichol en Wisconsin. Así es como los conceptos matemáticos deben explicarse y presentarse a los jueces, políticos y la sociedad: lo más claro y convincente posible.