Como sabemos, cualquier cuerpo que flote en un líquido tarde o temprano se detendrá debido a las fuerzas de fricción viscosa, si su movimiento no es soportado por ningún motor. Pero hay líquidos llamados superfluidos en los que la fricción viscosa está ausente
(*) . El ejemplo más famoso de un superfluido es
el helio líquido , enfriado al menos a 2,17 grados por encima de la temperatura cero absoluta.
El movimiento con una completa ausencia de viscosidad se manifiesta en muchos efectos impresionantes: el helio superfluido fluye fácilmente a través de las grietas y grietas más estrechas, es capaz de fluir sin fin en un círculo
(**) y fluir fuera de un recipiente a través de una delgada película líquida adherida a sus paredes. Todos estos fenómenos son ejemplos de efectos cuánticos a gran escala.
En un
artículo teórico reciente , se consideró la pregunta: ¿es posible nadar en un líquido superfluido? En otras palabras, ¿puede un nadador hipotético, moviendo sus brazos y piernas, crear una fuerza de tracción que le permita acelerar o reducir la velocidad sin usar la fuerza de la fricción viscosa?
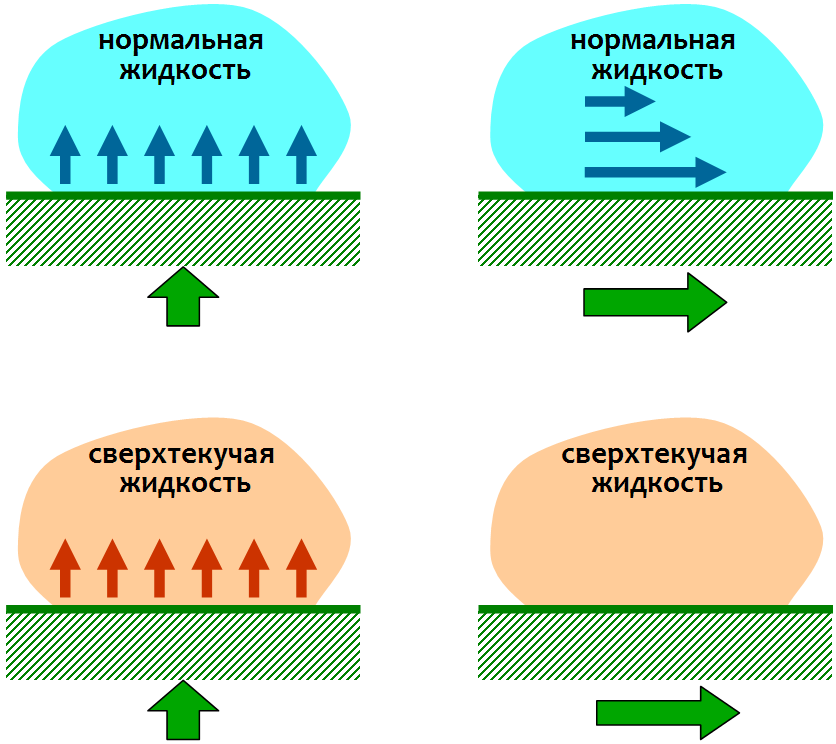
Uno puede darse cuenta de la no trivialidad de la respuesta a esta pregunta al considerar el comportamiento de los líquidos normales y superfluidos en interacción con los cuerpos. Como se muestra en la figura, se puede hacer que un fluido normal se mueva, empujándolo con la superficie de un cuerpo sólido y arrastrándolo consigo mismo debido a las fuerzas de fricción viscosas. En un líquido superfluido, este último no funcionará: no tiene fricción y solo se puede empujar, lo que, como veremos, hace que algunos métodos de natación sean imposibles.
Para analizar los principios generales de los fenómenos físicos, es habitual considerar modelos simples de "caballos esféricos en el vacío". El artículo en discusión no es una excepción: consideró a los "nadadores" modelo de dos y tres cuerpos, que son dos y tres elipsoides conectados por "articulaciones". Los nadadores pueden mover sus elipsoides, articulaciones dobladas y sin doblar. Si el nadador logra salir del fluido circundante, creará tracción y comenzará a moverse.
Un nadador de dos cuerpos parece un molusco bivalvo y puede intentar nadar cambiando periódicamente el ángulo entre sus elipsoides como una mariposa que agita sus alas. Sin embargo, los cálculos muestran que no podrá nadar: con una ola, el nadador se mueve hacia adelante y hacia atrás, pero en promedio permanece en su lugar (
aquí puede ver un video de sus movimientos simples).
Arriba: perfil de densidad del líquido superfluido en diferentes puntos en el tiempo. Las áreas azules de las que se expulsa el líquido son elipsoides de un nadador de dos cuerpos.
Abajo: la coordenada del nadador en función del tiempo.
Se pueden establecer paralelos entre estos resultados y
el teorema de vieira de Purcell . Este importante teorema de la teoría de la natación dice que un molusco bivalvo, que abre y cierra lentamente su caparazón en un líquido viscoso, no flotará en ninguna parte, siempre que sus movimientos sean reversibles en el tiempo. Esto último significa que la apertura y el cierre periódicos de las aletas de la carcasa no cambian su apariencia cuando el tiempo comienza en la dirección opuesta (puede imaginar un video que mira hacia atrás de la misma manera que durante la reproducción normal). En nuestro caso, el líquido no tiene viscosidad, y no es el teorema de Purcell lo que funciona, sino su análogo para un líquido superfluido.
Dibujo de un informe de Edward Purcell (Premio Nobel de Física en 1952).La situación cambia cuando un nadador de dos cuerpos comienza a balancear sus elipsoides con mayor frecuencia. Si su velocidad excede la velocidad del sonido en un líquido, comienzan a emitirse ondas de sonido y vórtices
(***) . Estas excitaciones llevan consigo un cierto impulso que, debido al retroceso, hace que el nadador se mueva. La figura muestra que en este caso, su coordenada fluctúa, pero en general disminuye con el tiempo, lo que significa que el nadador se mueve de derecha a izquierda. Después de diez fluctuaciones (a la derecha de la línea punteada en el gráfico), la aleta se detiene y el nadador continúa moviéndose por inercia (
video ).
Puede intentar otro tipo de movimiento del nadador, cuando sus alas se cierran y se separan no solo en la dirección correcta, sino alternativamente en dos direcciones. Tales movimientos simétricos son similares a las aletas de una mariposa. Los cálculos muestran que, en este caso, muchos vórtices cuantificados están excitados (son visibles en la figura como círculos pequeños), pero, en general, la natación no es muy efectiva. La razón es que aproximadamente la misma cantidad de vórtices se excitan, se mueven hacia la derecha y hacia la izquierda, y los pulsos que se llevan se cancelan en gran medida (
video ).
Considere ahora un nadador de tres cuerpos. Tiene una ventaja importante sobre el cuerpo de dos cuerpos: puede retorcerse y hacer movimientos serpentinos que no pasan a sí mismos cuando el tiempo se invierte. Esto significa que el teorema de Purcell no se aplica a él, y debe nadar incluso con movimientos lentos. Los cálculos que se muestran en la figura confirman esta conjetura: cuando se mueve, el nadador se mueve con confianza horizontalmente, mientras se mueve ligeramente verticalmente (
video ).
Arriba: perfil de densidad del líquido superfluido en diferentes puntos en el tiempo. Las áreas azules donde se expulsa el líquido son los elipsoides del nadador de tres cuerpos.
Abajo: coordenadas horizontales (X) y verticales (Y) del nadador en función del tiempo.¿Qué aplicación se puede encontrar a los resultados obtenidos? Parece que la tarea de nadar en un superfluido no es particularmente relevante en la práctica, pero hay un área donde puede ser útil. Recientemente, se han desarrollado activamente experimentos con condensación de Bose y superfluidez de
gases atómicos ultrafríos , con los cuales existen grandes planes para crear simuladores cuánticos, computadoras cuánticas y modelos experimentales de estados exóticos de la materia. En tales sistemas, es posible crear coágulos de un gas superfluido de un tipo sumergido en un gas superfluido de otro tipo. Si podemos deformar el grupo como lo necesitamos (y esto se puede hacer con la ayuda de rayos láser), entonces será posible hacer que este grupo nade, a partir del gas circundante. La figura muestra los cálculos que demuestran esta posibilidad: cuando los cambios en la forma del grupo no son reversibles en el tiempo, realmente logra moverse (
video ).
Entonces, vemos que es necesario nadar en un fluido superfluido sabiamente: el teorema de Purcell garantiza que no podemos nadar si nuestros movimientos de brazos y piernas coinciden con nosotros cuando jugamos en la dirección opuesta. Para comenzar a movernos, necesitaremos movernos más rápido que el sonido (lo cual es problemático), o movernos como una serpiente, interrumpiendo la reversibilidad de los movimientos a tiempo. Estas conclusiones son bien conocidas por los microorganismos que flotan en un líquido viscoso: para eludir el teorema de Purcell, tienen que usar flagelos giratorios en espiral, que son análogos del nadador de tres cuerpos considerado aquí.
Según el artículo :
Hiroki Saito, ¿Podemos nadar en superfluidos?: Demostración numérica de autopropulsión en un Bose - Einstein Condensate, Journal of the Physical Society of Japan 84, 114001 (2015).(*) De hecho, esto no es del todo cierto: cualquier líquido superfluido real puede representarse como una combinación de los componentes "normal" y superfluido ( modelo de dos fluidos ), y el componente normal aún ralentizará el cuerpo en movimiento. Sin embargo, esto no evita que el componente superfluido se mueva completamente sin fricción.
(**) En la práctica, el flujo circular de helio superfluido puede atenuarse, pero no debido a la viscosidad, sino debido al proceso de mecánica cuántica: el deslizamiento de los vórtices cuantificados. No se observó una atenuación notable en los experimentos durante 18 horas.
(***) Los vórtices que surgen en un superfluido no son solo vórtices como pequeños tornados, sino excitaciones topológicas cuantificadas . A diferencia de los vórtices ordinarios, no pueden desaparecer simplemente debido a la atenuación gradual del flujo.