Enredo cuántico sin confusión: ¿qué es?

Introduccion

Han aparecido muchos artículos populares que hablan sobre enredos cuánticos. Los experimentos con entrelazamiento cuántico son bastante espectaculares, pero no se otorgan con premios. ¿Por qué los experimentos tan interesantes para el profano no son de interés para los científicos? Los artículos populares hablan sobre las sorprendentes propiedades de los pares de partículas enredadas: la exposición a una de ellas conduce a un cambio instantáneo en el estado de la segunda. Y lo que está oculto detrás del término "teletransportación cuántica", sobre el cual ya han comenzado a decir que está sucediendo a una velocidad superluminal. Miremos todo esto desde el punto de vista de la mecánica cuántica normal.

Lo que viene de la mecánica cuántica

Las partículas cuánticas pueden estar en dos tipos de estados, según el clásico libro de texto de Landau y Lifshitz: puro y mixto. Si una partícula no interactúa con otras partículas cuánticas, se describe mediante una función de onda que depende solo de sus coordenadas o momentos; este estado se llama puro. En este caso, la función de onda obedece a la ecuación de Schrödinger. Otra opción es posible: la partícula interactúa con otras partículas cuánticas. En este caso, la función de onda ya se refiere a todo el sistema de partículas que interactúan y depende de todas sus variables dinámicas. Si estamos interesados ​​en una sola partícula, su estado, como mostró Landau hace 90 años, puede ser descrito por un operador de matriz u densidad. La matriz de densidad obedece a una ecuación similar a la ecuación de Schrödinger



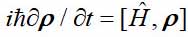
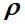
donde Es la matriz de densidad, H es el operador de Hamilton, y los corchetes denotan el conmutador.

Landau lo sacó. Cualquier cantidad física relacionada con una partícula dada puede expresarse a través de una matriz de densidad. Esta condición se llama mixta. Si tenemos un sistema de partículas que interactúan, entonces cada una de las partículas está en un estado mixto. Si las partículas se dispersaron a grandes distancias y la interacción desapareció, su estado seguirá siendo mixto. Si cada una de varias partículas está en estado puro, entonces la función de onda de dicho sistema es el producto de las funciones de onda de cada una de las partículas (si las partículas son diferentes. Para partículas, bosones o fermiones idénticos, es necesario hacer una combinación simétrica o antisimétrica, ver [1], pero más tarde, la identidad de partículas, fermiones y bosones ya es una teoría cuántica relativista.

Un estado entrelazado de un par de partículas es un estado en el que existe una correlación constante entre cantidades físicas relacionadas con diferentes partículas. Un ejemplo simple y más común es una cierta cantidad física total, por ejemplo, el giro total o el momento angular de un par. Un par de partículas está en un estado puro, pero cada una de las partículas está en un estado mixto. Puede parecer que un cambio en el estado de una partícula afectará inmediatamente el estado de otra partícula. Incluso si se dispersaron lejos y no interactúan, esto es lo que se expresa en artículos populares. Este fenómeno ya se ha denominado teletransportación cuántica. Algunos periodistas analfabetos incluso afirman que el cambio ocurre instantáneamente, es decir, se propaga más rápido que la velocidad de la luz.

Considere esto desde el punto de vista de la mecánica cuántica: en primer lugar, cualquier acción o medida que cambie el giro o el momento angular de una sola partícula viola inmediatamente la ley de conservación de la característica total. El operador correspondiente no puede conmutar con giro completo o momento angular completo. Por lo tanto, se viola el enredo inicial del estado de un par de partículas. El giro o momento de la segunda partícula ya no puede asociarse inequívocamente con el de la primera. Puedes considerar este problema desde el otro lado. Después de que la interacción entre las partículas ha desaparecido, la evolución de la matriz de densidad de cada una de las partículas se describe mediante su propia ecuación, en la que no se incluyen las variables dinámicas de las otras partículas. Por lo tanto, la exposición a una partícula no cambiará la matriz de densidad a otra.

Incluso existe el teorema de Eberhard [2], que afirma que la influencia mutua de dos partículas no puede detectarse mediante mediciones. Que haya un sistema cuántico, que se describe mediante una matriz de densidad. Y dejemos que este sistema consista en dos subsistemas A y B. El teorema de Eberhard establece que ninguna medición de observables relacionados solo con el subsistema A no afecta el resultado de medir cualquier observable que esté relacionado solo con el subsistema B. Sin embargo, la prueba del teorema utiliza la hipótesis de reducción de onda una función que no ha sido probada ni teórica ni experimentalmente. Pero todas estas consideraciones se hacen en el marco de la mecánica cuántica no relativista y se relacionan con varias partículas no idénticas.

Estas consideraciones no funcionan en la teoría relativista en el caso de un par de partículas idénticas. Permítanme recordarles una vez más que la identidad o la indistinguibilidad de las partículas proviene de la mecánica cuántica relativista, donde el número de partículas no se conserva. Sin embargo, para partículas lentas, podemos usar un aparato más simple de mecánica cuántica no relativista, simplemente teniendo en cuenta la indistinguibilidad de las partículas. Entonces, la función de onda del par debe ser simétrica (para bosones) o antisimétrica (para fermiones) con respecto a la permutación de las partículas. Tal requisito surge en la teoría relativista, independientemente de las velocidades de las partículas. Es este requisito el que conduce a correlaciones de largo alcance de un par de partículas idénticas. En principio, un protón con un electrón también puede estar en un estado enredado. Sin embargo, si se dispersan por varias decenas de angstroms, la interacción con campos electromagnéticos y otras partículas destruirá este estado. La interacción de intercambio (como se llama a este fenómeno) actúa a distancias macroscópicas, como lo demuestran los experimentos. Un par de partículas, incluso dispersas por metros, permanece indistinguible. Si está realizando una medición, entonces no sabe exactamente a qué partícula pertenece el valor medido. Estás tomando medidas con un par de partículas al mismo tiempo. Por lo tanto, todos los experimentos espectaculares se llevaron a cabo con exactamente las mismas partículas: electrones y fotones. Estrictamente hablando, este no es el estado confuso que se considera en el marco de la mecánica cuántica no relativista, sino algo similar.

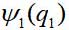
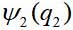
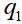
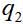
Considere el caso más simple: un par de partículas idénticas que no interactúan. Si las velocidades son pequeñas, podemos utilizar la mecánica cuántica no relativista, teniendo en cuenta la simetría de la función de onda con respecto a la permutación de partículas. Deje que la onda funcione de la primera partícula , la segunda partícula - donde y - variables dinámicas de la primera y segunda partículas, en el caso más simple, solo las coordenadas. Entonces la función de onda del par



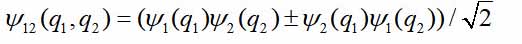
Los signos + y - se refieren a bosones y fermiones. Supongamos que las partículas están muy separadas. Entonces localizados en áreas remotas 1 y 2, respectivamente, es decir, fuera de estas áreas son pequeños. Intentemos calcular el valor promedio de alguna variable de la primera partícula, por ejemplo, la coordenada. Por simplicidad, podemos imaginar que solo las coordenadas están incluidas en las funciones de onda. Resulta que el valor promedio de las coordenadas de la partícula 1 se encuentra ENTRE las regiones 1 y 2, y coincide con el valor promedio de la partícula 2. Esto es realmente natural: las partículas son indistinguibles, no podemos saber qué partícula se miden las coordenadas. En general, todos los valores promedio para las partículas 1 y 2 serán los mismos. Esto significa que al mover la región de localización de la partícula 1 (por ejemplo, la partícula se localiza dentro del defecto de la red cristalina y movemos todo el cristal), actuamos sobre la partícula 2, aunque las partículas no interactúan en el sentido habitual, a través de un campo electromagnético, por ejemplo. Este es un ejemplo simple de enredo relativista.

No se produce transferencia instantánea de información debido a estas correlaciones entre las dos partículas. El aparato de la teoría cuántica relativista se construyó originalmente para que los eventos en el espacio-tiempo en lados opuestos del cono de luz no puedan influenciarse entre sí. En pocas palabras, sin señal, sin influencia o perturbación puede propagarse más rápido que la luz. Ambas partículas son en realidad un estado de un campo, por ejemplo, electrón-positrón. Al actuar en el campo en un punto (en la partícula 1), creamos una perturbación que se propaga como ondas de agua. En la mecánica cuántica no relativista, la velocidad de la luz se considera infinitamente grande, lo que crea la ilusión de un cambio instantáneo.

La situación en la que las partículas espaciadas a largas distancias permanecen acopladas en pares parece paradójica debido a las ideas clásicas sobre partículas. Debemos recordar que en realidad no hay partículas, sino campos. Lo que representamos como partículas es simplemente el estado de estos campos. La idea clásica de partículas es completamente inadecuada en el micromundo. Inmediatamente surgen preguntas sobre el tamaño, la forma, el material y la estructura de las partículas elementales. De hecho, situaciones paradójicas para el pensamiento clásico surgen con una partícula. Por ejemplo, en el experimento Stern-Gerlach, un átomo de hidrógeno vuela a través de un campo magnético no homogéneo dirigido perpendicularmente a la velocidad. El giro del núcleo puede descuidarse debido a la pequeñez del magneton nuclear; deje que el giro del electrón se dirija inicialmente a lo largo de la velocidad.



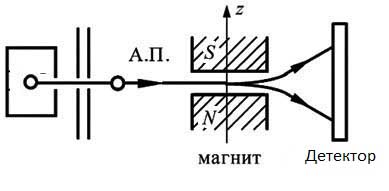
La evolución de la función de onda atómica es fácil de calcular. El paquete de onda localizada inicial se divide en dos idénticos, volando simétricamente en ángulo con respecto a la dirección original. Es decir, un átomo, una partícula pesada, generalmente considerada clásica con una trayectoria clásica, dividida en dos paquetes de ondas que pueden dispersarse a distancias completamente macroscópicas. Al mismo tiempo, observo: se deduce del cálculo que incluso un experimento ideal de Stern-Gerlach no puede medir el giro de las partículas.

Si el detector se une a un átomo de hidrógeno, por ejemplo, químicamente, entonces las "mitades", dos paquetes de ondas dispersas, se ensamblan en uno. Cómo ocurre tal localización de la partícula manchada es una teoría existente por separado en la que no entiendo. Los interesados ​​pueden encontrar una extensa literatura sobre este tema.

Conclusión

Surge la pregunta: ¿cuál es el objetivo de numerosos experimentos para demostrar correlaciones entre partículas a grandes distancias? Además de confirmar la mecánica cuántica, que ningún físico normal ha dudado durante mucho tiempo, esta es una demostración espectacular que impresiona a los funcionarios públicos y aficionados que asignan fondos para la ciencia (por ejemplo, Gazprombank patrocina el desarrollo de líneas de comunicación cuántica). Para la física, estas demostraciones costosas no dan nada, aunque permiten el desarrollo de técnicas experimentales.

Literatura
1. Landau, L. D., Lifshits, E. M. Mecánica cuántica (teoría no relativista). - 3ª edición, revisada y complementada. - M .: Nauka, 1974.- 752 p. - ("Física teórica", Volumen III).
2. Eberhard, PH, "Teorema de Bell y los diferentes conceptos de no localidad", Nuovo Cimento 46B, 392-419 (1978)