“Hay dos bolas idénticas a la misma temperatura. Uno de ellos se encuentra en una superficie horizontal, el otro está suspendido en un hilo. Ambas bolas informan la misma cantidad de calor. ¿Las bolas serán las mismas después de esto o no? (Cualquier tipo de pérdida de calor puede descuidarse) ".

Tal problema a veces se puede encontrar en las olimpiadas de física y redes sociales . La respuesta generalmente aceptada es intuitiva: debido al consumo de energía para la expansión térmica en presencia de gravedad, una bola que descansa sobre una superficie horizontal estará más fría que colgada de un hilo. Un artículo reciente mostró que esta respuesta es incorrecta. De hecho, el resultado será el opuesto: la bola que miente será más cálida que la que cuelga. Entenderemos por qué el método tradicional de resolver este problema conduce a una respuesta incorrecta y por qué la intuición en este caso nos deprime.

La solución tradicional y su problema.

La solución tradicional se basa en la siguiente línea de razonamiento. Ambas bolas se expandirán durante el calentamiento, debido a esto, el centro de masa de la bola que descansa sobre una superficie horizontal se elevará ligeramente, y el centro de masa de la bola que cuelga caerá. Como resultado, la bola acostada se calienta más débilmente, ya que parte del calor transferido a ella se gastará en su subida, y la bola colgante se calentará más debido al trabajo de gravedad adicional cuando se baja.


Razonamiento utilizado en la solución tradicional: debido a la expansión térmica, la bola que descansa sobre la mesa se eleva y la bola que cuelga del hilo se baja.

La respuesta puede expresarse mediante una fórmula simple para la diferencia de temperatura que miente ( $$ ) y colgando ( $$ ) bolas:

$$

donde $$ , $$ y $$ - masa, radio y capacidad calorífica de las bolas, $$ - la cantidad de calor que se les transfiere, $$ - aceleración de la gravedad, $$ Es el coeficiente de expansión térmica lineal del material de las bolas, que consideramos suficientemente pequeño. Como se ve $$ - la bola que miente será más fría.

Parecería que en esta decisión todo es lógico. El "primer trago", que demuestra que algo anda mal aquí, es un intento mental de crear un motor de calor sobre la base de la pelota.

La máquina puede funcionar de la siguiente manera: primero, la pelota descansa sobre la mesa, donde la calentamos, por lo que su centro de masa se eleva. Luego fijamos la bola en el hilo que cuelga en la parte superior y retiramos cuidadosamente la mesa para que la altura de la bola no cambie. Finalmente, enfriamos la bola a su temperatura inicial, como resultado, la bola se comprime y su centro de masa se eleva. En pocas palabras: la parte del calor que transferimos a la pelota cuando se calentó se convirtió en un trabajo mecánico para elevarla, y este ciclo se puede repetir sin cesar.


El ciclo de operación de un motor térmico basado en bolas: después de calentar y enfriar, la bola se levantó, lo que significa que convertimos parte del calor en trabajo mecánico.

El problema aquí es que al aumentar el radio de la pelota, la eficiencia (eficiencia) de una máquina de este tipo puede hacerse arbitrariamente cerca del 100%. Esto contradice la segunda ley de la termodinámica , según la cual la eficiencia de un motor térmico no puede exceder la eficiencia del ciclo de Carnot a las mismas temperaturas del calentador y el refrigerador.

Cual es el problema

¿Por qué la solución tradicional al problema es incorrecta? Aquí es necesario tener en cuenta que la bola que yace sobre la mesa desde el principio, antes de que se caliente, será aplanada ligeramente por la gravedad, y la bola colgante se estirará ligeramente. Esto afectará negativamente la eficiencia del motor térmico descrito anteriormente: durante la suspensión, la bola bajará ligeramente, debido a esto la eficiencia disminuirá y ya no excederá la eficiencia del ciclo de Carnot.


El efecto de la gravedad en las bolas: la bola que descansa sobre la mesa se aplana y la que cuelga del hilo se estira.

¿Cómo se manifestará esto al considerar el problema original? Resulta que comprimir o estirar un material cambia su capacidad calorífica: en el caso de un material comprimido, calentar a la misma temperatura requerirá menos calor que en el caso de un material estirado. Por lo tanto:

• Cuando la bola que está sobre la mesa se calienta, parte del calor aumentará debido a la expansión térmica; pero, junto con esto, el calentamiento del material de la bola en sí será más fácil y requerirá menos calor.
• Cuando una bola que cuelga de un hilo se calienta, el trabajo de la gravedad cuando se baja se agregará al calor que se le transfiere; pero, junto con esto, calentar el material de la bola requerirá más tiempo y requerirá más calor.

En la solución tradicional, solo se tienen en cuenta los factores indicados por las flechas blancas. Ignorar los factores mostrados por las flechas negras conduce a una respuesta errónea.

Como podemos ver, en ambos casos hay factores que funcionan tanto a favor de una respuesta (la bola de mentira puede resultar más fría que la que cuelga) como en la dirección opuesta (la bola de mentira puede ser más cálida que la que cuelga). ¿Cuál domina?

Parecería que el efecto de cambiar la capacidad de calor de un material durante la compresión o la tensión, incluso si existe, debería ser muy pequeño y puede descuidarse, como se hace en la solución tradicional del problema. Sin embargo, esto no es así. Este efecto es del mismo orden de pequeñez que la expansión térmica en sí, ya que ambos efectos provienen de la anarmonía de las fuerzas interatómicas. Tener en cuenta uno de estos efectos en la solución tradicional combinada con ignorar el otro es inconsistente y conduce a una respuesta errónea.

El artículo muestra que con la solución correcta al problema, la diferencia de temperatura de las bolas después de transferirles la misma cantidad de calor es igual a:

$$

donde $$ - la temperatura absoluta de las bolas, $$ - la tasa de cambio del coeficiente de expansión térmica del material de las bolas con un cambio en su temperatura.

En comparación con el resultado de la solución tradicional, la diferencia de temperatura es:

• El signo opuesto, ya que para la mayoría de los materiales el valor $$ es positivo, por lo tanto, todo el lado derecho de la igualdad también es positivo, y $$ .
• Mucho más pequeño en valor absoluto, ya que aquí en lugar de un valor pequeño aparecen valores aún más pequeños $$ y $$ .

Por lo tanto, los dos efectos discutidos anteriormente se cancelan casi por completo, pero el segundo de ellos (cambio en la capacidad de calor durante la compresión o la tensión) es ligeramente más fuerte que el primero (expansión térmica).

Anarmonicidad de las fuerzas interatómicas.

Los autores del artículo llevan a cabo una consideración bastante rigurosa del problema, pero, desafortunadamente, no proporcionan una explicación clara de cómo se produce la compensación casi completa de los dos efectos, por lo que tuve que lidiar con este problema yo mismo.

La figura muestra una dependencia típica de la energía potencial de la interacción atómica en la distancia entre ellos. La fuerza que actúa sobre los átomos se dirige hacia una disminución en la energía potencial; por lo tanto, los átomos se repelen fuertemente entre sí a distancias pequeñas y son atraídos débilmente a grandes distancias. A cierta distancia $$ La energía potencial alcanza un mínimo. El deseo de los átomos a esta distancia energéticamente más ventajosa es la razón de su unión a moléculas, líquidos y sólidos.


Ahora veamos de dónde viene la expansión térmica de los materiales. Con el movimiento térmico caótico, la distancia entre los átomos ya no es estrictamente igual $$ , y fluctúa cerca de este valor. El enlace entre los átomos tiene la propiedad del anarmonismo: se comporta como un resorte asimétrico, que es más fácil de estirar que de comprimir. Como resultado, durante el movimiento térmico, la unión se estira la mayor parte del tiempo, en lugar de comprimirse, por lo que la distancia promedio $$ entre átomos se convierte en más de $$ . Con el aumento de la temperatura, este efecto se intensifica, las distancias entre los átomos aumentan y el material se expande.


La razón de la expansión térmica de los materiales: durante el movimiento térmico, la distancia promedio entre los átomos aumenta debido a la anarmonía de las fuerzas de interacción interatómica.

¿Qué sucede cuando el material se comprime o estira, como en el caso de bolas aplastadas o estiradas? Cuando un material se comprime, una fuerza externa disminuye la distancia promedio entre los átomos, y cuando se estira, aumenta.


Bajo compresión, la distancia de equilibrio entre los átomos disminuye, mientras que bajo tensión aumenta.

Ahora estamos listos para comprender cómo la compresión y la tensión de un material afectan su capacidad calorífica. Imagine que exprimimos el material, de modo que la distancia entre los átomos durante el movimiento térmico ahora oscila cerca de la posición de equilibrio desplazada hacia la izquierda. En este caso, el anarmonismo no ha desaparecido, por lo tanto, como antes, cuando se calienta, la distancia promedio entre los átomos aumentará. Pero al mismo tiempo, volveremos al mínimo de energía potencial, lo que significa que la energía del material disminuirá aún más. Esto explica la disminución en la capacidad de calor del material durante la compresión: la expansión térmica conduce a una pequeña disminución adicional en la energía de las interacciones interatómicas, por lo tanto, se requiere menos energía para calentar el material.



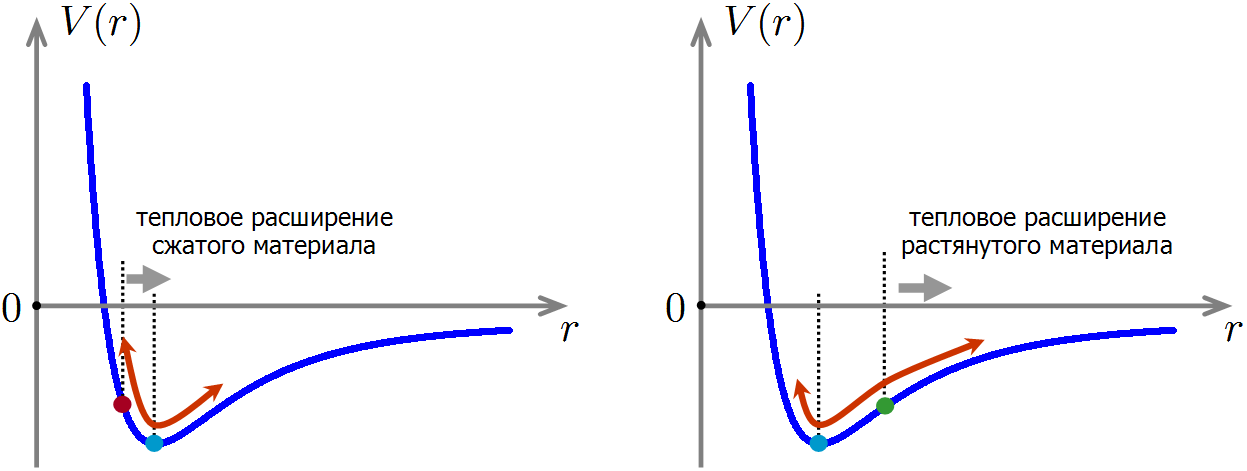
Si el material se estira, la situación es la opuesta: con la expansión térmica, la energía de interacción de los átomos crecerá más rápido que en el material sin estirar. Por lo tanto, para calentar el material estirado a la misma temperatura, se requiere un poco más de energía que sin estirar, lo que significa que la capacidad calorífica del material estirado será mayor.

Entonces, en el ejemplo del problema de la olimpiada, que durante muchas décadas se ha resuelto (y, tal vez, se sigue resolviendo) erróneamente, vemos que la física real a veces contradice nuestra intuición. Por lo tanto, es tan importante al resolver problemas usar cuidadosamente el aparato matemático, no limitado al razonamiento superficial.

Según el artículo :

Giacomo De Palma, Mattia C. Sormani, efecto contraintuitivo de la gravedad sobre la capacidad calorífica de una esfera sólida: reexamen de un problema bien conocido, American Journal of Physics 83, 723 (2015).
Preimpresión pública del artículo: arxiv.org/pdf/1502.01337