Flujo linealizado característico de una turbina de vapor. Parte 2. Ejemplo de construcción para la turbina PT-80 en MATLAB

Prefacio a la primera parte

Modelar turbinas de vapor es una tarea diaria para cientos de personas en nuestro país. En lugar de la palabra modelo, se acostumbra decir una característica de gasto . Las características de consumo de las turbinas de vapor se utilizan para resolver problemas tales como el cálculo del consumo específico de combustible equivalente para electricidad y calor producido por las centrales térmicas; optimización del CHP; planificación y mantenimiento de modos de centrales térmicas.

He desarrollado una nueva característica de flujo de una turbina de vapor : una característica de flujo linealizado de una turbina de vapor. La característica de flujo desarrollada es conveniente y efectiva para resolver estos problemas. Sin embargo, por el momento se describe solo en dos artículos científicos:

1. Optimización de la operación de centrales térmicas en las condiciones del mercado mayorista de energía eléctrica y capacidad de Rusia ;
2. Métodos computacionales para determinar el consumo específico de combustible equivalente de las centrales térmicas para la energía eléctrica y térmica suministrada en el modo de generación combinada .

Y ahora en mi blog me gustaría:

• en primer lugar, en un lenguaje simple y accesible para responder las preguntas básicas sobre la nueva característica de caudal (ver. Característica de caudal lineal de una turbina de vapor. Parte 1. Preguntas básicas );
• segundo, proporcione un ejemplo de construcción de una nueva característica de flujo que ayudará a comprender tanto el método de construcción como las propiedades de la característica (ver más abajo);
  
• en tercer lugar, refutar dos afirmaciones bien conocidas sobre los modos de operación de una turbina de vapor (ver. Características de flujo linealizado de una turbina de vapor. Parte 3. Disipar mitos sobre el funcionamiento de una turbina de vapor ).
  

1. Los datos de origen

Los datos iniciales para construir una característica de flujo linealizado pueden ser

1. valores de potencia real Q ₀ , N, Q _p , Q _t medidos durante el funcionamiento de la turbina de vapor,
2. nomogramas q _t brutos de la documentación normativa y técnica.

Por supuesto, los valores instantáneos reales de Q ₀ , N, Q _p , Q _t son datos fuente ideales. Recopilar dichos datos lleva mucho tiempo.

En los casos en que los valores reales de Q ₀ , N, Q _p , Q _t no _estén disponibles, puede procesar nomogramas q _t brutos. Ellos, a su vez, se obtuvieron sobre la base de mediciones. Lea más sobre las pruebas de turbinas en VM Gornstein y otros métodos para optimizar los modos de los sistemas de energía .

2. El algoritmo para construir características de flujo linealizado

El algoritmo de construcción consta de tres pasos.

1. Traducción de nomogramas o resultados de medición en una vista tabular.
2. Linealización del flujo característico de una turbina de vapor.
3. Determinación de los límites del rango de control de la turbina de vapor.

Cuando se trabaja con nomogramas q _t bruto, el primer paso es rápido. Este trabajo se llama digitalización . La digitalización de 9 nomogramas para el ejemplo actual me llevó unos 40 minutos.

El segundo y tercer paso requieren el uso de paquetes matemáticos. Amo y uso MATLAB por muchos años. Mi ejemplo de construcción de una característica de flujo linealizado se hace en él. Se puede descargar un ejemplo desde el enlace , ejecutar y descubrir de forma independiente el método de construcción de una característica de flujo linealizado.

La característica de flujo para la turbina en cuestión fue construida para los siguientes valores fijos de los parámetros de modo:

• operación de una etapa
• presión media vapor presión = 13 kgf / cm2,
• presión de vapor a baja presión = 1 kgf / cm2.

Contenido del archivo Chuchueva-PT-80-linear-feature-curve.rar .

1) Nomogramas de consumo específico qt bruto para la generación de electricidad (los puntos rojos marcados se digitalizan, se transfieren a la tabla):

• PT80_qt_Qm_eq_0_digit.png,
• PT80_qt_Qm_eq_100_digit.png,
• PT80_qt_Qm_eq_120_digit.png,
• PT80_qt_Qm_eq_140_digit.png,
• PT80_qt_Qm_eq_150_digit.png,
• PT80_qt_Qm_eq_20_digit.png,
• PT80_qt_Qm_eq_40_digit.png,
• PT80_qt_Qm_eq_60_digit.png,
• PT80_qt_Qm_eq_80_digit.png.

2) El resultado de la digitalización (cada archivo csv corresponde a un archivo png):

• PT-80_Qm_eq_0.csv,
• PT-80_Qm_eq_100.csv,
• PT-80_Qm_eq_120.csv,
• PT-80_Qm_eq_140.csv,
• PT-80_Qm_eq_150.csv,
• PT-80_Qm_eq_20.csv,
• PT-80_Qm_eq_40.csv,
• PT-80_Qm_eq_60.csv,
• PT-80_Qm_eq_80.csv.

3) Script MATLAB con cálculos y gráficos:

• PT_80_linear_characteristic_curve.m

4) El resultado de digitalizar los nomogramas y el resultado de construir una característica de flujo linealizado en forma tabular:

• PT_80_linear_characteristic_curve.xlsx.

Paso 1. Traducción de nomogramas o resultados de medición a una vista tabular

1. Procesamiento de datos fuente

Los datos iniciales para nuestro ejemplo son nomogramas q _t brutos.

Para digitalizar muchos nomogramas, necesita una herramienta especial. Repetidamente he usado una aplicación web para estos propósitos. La aplicación es simple, conveniente, pero no tiene suficiente flexibilidad para automatizar el proceso. Parte del trabajo debe hacerse manualmente.

En este paso, es importante digitalizar los puntos extremos de los nomogramas que definen los límites del rango de ajuste de la turbina de vapor .

El trabajo consistía en marcar los puntos de la característica de descarga en cada archivo png utilizando la aplicación , descargar el csv resultante y recopilar todos los datos en una tabla. El resultado de la digitalización se puede encontrar en el archivo PT-80-linear-característica-curva.xlsx, hoja "PT-80", tabla "Datos de entrada".

2. Traer unidades de medida a unidades de poder

A continuación, en la hoja "PT-80" calculamos los valores de Q _{0 de} acuerdo con la fórmula

$$$$ display $$ \ begin {ecation} Q_0 = \ frac {q_T \ cdot N} {1000} + Q_P + Q_T \ qquad (1) \ end {ecation} $$ display $$

y traemos todos los valores iniciales a MW. Los cálculos se implementan utilizando MS Excel.

La tabla resultante "Datos de entrada (unidad de potencia)" es el resultado del primer paso del algoritmo.

Paso 2. Linealización de la característica de flujo de la turbina de vapor.

1. Prueba de MATLAB

En este paso, debe instalar y abrir la versión de MATLAB no inferior a 7.3 (esta es una versión anterior, actual 8.0). En MATLAB, abra el archivo PT_80_linear_characteristic_curve.m, ejecútelo y asegúrese de que esté funcionando. Todo funciona correctamente, si sobre los resultados de ejecutar el script en la línea de comando ve el siguiente mensaje:

    PT_80_linear_characteristic_curve.xlsx  1  : a(N) = 2.317, a(Q) = 0.621, a(Q) = 0.255, a0 = 33.874   = 0.006, (0.57%)      = 37 

Si tiene algún error, descubra por sí mismo cómo solucionarlo.

2. Cálculos

Todos los cálculos se implementan en el archivo PT_80_linear_characteristic_curve.m. Consideremoslo en partes.

1) Indicamos el nombre del archivo fuente, la hoja, el rango de celdas que contiene la tabla "Datos fuente (unidad de capacidad)" obtenida en el paso anterior.

 XLSFileName = 'PT_80_linear_characteristic_curve.xlsx'; XLSSheetName = 'PT-80'; XLSRange = 'F3:I334'; 

2) Leemos los datos de origen en MATLAB.

 sourceData = xlsread(XLSFileName, XLSSheetName, XLSRange); N = sourceData(:,1); Qm = sourceData(:,2); Ql = sourceData(:,3); Q0 = sourceData(:,4); fprintf('    %s  %1.0f \n', XLSFileName, toc); 

Usamos la variable Qm para el caudal promedio de vapor Q _p , el índice m desde el medio es promedio; de manera similar, usamos la variable Ql para flujo de vapor a baja presión Q _n , el índice l desde bajo es bajo.

3) Definir los coeficientes α _i .

Recordemos la fórmula general de las características del flujo.

$$$$ display $$ \ begin {ecation} Q_0 = f (N, Q_, Q_) \ qquad (2) \ end {ecation} $$ display $$

y especifique variables independientes (x_digit) y dependientes (y_digit).

 x_digit = [N Qm Ql ones(size(N,1),1)]; %  N,   Q,   Q,   y_digit = Q0; %    Q0 

Si no comprende por qué la matriz x_digit tiene un solo vector (última columna), lea los materiales de regresión lineal. Sobre el tema del análisis de regresión, recomiendo el libro Draper N., Smith H. Análisis de regresión aplicado . Nueva York: Wiley, en prensa, 1981. 693 p. (disponible en ruso).

Ecuación de flujo linealizado característico de una turbina de vapor

$$$$ display $$ \ begin {ecation} Q_0 = \ alpha_N \ cdot N + \ alpha_ \ cdot Q_ + \ alpha_ \ cdot Q_ + \ alpha_0 \ qquad (3) \ end {ecuación} $$ display $$

es un modelo de regresión lineal múltiple. Los coeficientes α _i se determinarán utilizando el "gran beneficio de la civilización" , el método de mínimos cuadrados. Por separado, observo que el método de mínimos cuadrados fue desarrollado por Gauss en 1795.

En MATLAB, esto se hace en una línea.

 A = regress(y_digit, x_digit); fprintf(': a(N) = %4.3f, a(Q) = %4.3f, a(Q) = %4.3f, a0 = %4.3f\n',... A); 

La variable A contiene los coeficientes deseados (vea el mensaje en la línea de comando de MATLAB).

Por lo tanto, la característica de flujo linealizado obtenido de la turbina de vapor PT-80 tiene la forma

$$$$ display $$ \ begin {ecation} Q_0 = 2.317 \ cdot N + 0.621 \ cdot Q_ + 0.255 \ cdot Q_ + 33.874 \ qquad (4) \ end {ecation} $$ display $$

4) Estimamos el error de linealización de la característica de flujo obtenida.

 y_model = x_digit * A; err = abs(y_model - y_digit) ./ y_digit; fprintf('  = %1.3f, (%4.2f%%)\n\n', mean(err), mean(err)*100); 

El error de linealización es 0.57% (vea el mensaje en la línea de comando de MATLAB).

Para evaluar la conveniencia de usar las características de flujo linealizado de una turbina de vapor, resolvemos el problema de calcular el flujo de vapor de alta presión Q ₀ a valores de carga conocidos N, Q _p , Q _t .

Sea N = 82.3 MW, Q _p = 55.5 MW, Q _t = 62.4 MW, entonces

$$$$ display $$ \ begin {ecation} Q_0 = 2.317 \ cdot 82.3 + 0.621 \ cdot 55.5 + 0.255 \ cdot 62.4 + 33.874 = 274.9 \ qquad (5) \ end {ecuación} $$ mostrar $$

Permítame recordarle que el error de cálculo promedio es 0.57%.

Volvamos a la pregunta, ¿por qué la característica de flujo linealizado de una turbina de vapor es fundamentalmente más conveniente que los nomogramas de consumo específico q _t bruto para la generación de electricidad? Para comprender la diferencia fundamental en la práctica, resuelve dos problemas.

1. Calcule Q ₀ con la precisión indicada utilizando los nomogramas y sus ojos.
2. Automatice el proceso de cálculo de Q ₀ usando nomogramas.

Obviamente, en la primera tarea, la determinación de los valores brutos q por ojo está plagada de errores graves.

La segunda tarea es engorrosa de automatizar. Dado que los valores q q son groseramente no lineales , para dicha automatización el número de puntos digitalizados es diez veces mayor que en el ejemplo actual. La digitalización por sí sola no es suficiente, también es necesario implementar un algoritmo para interpolar (encontrar valores entre puntos) de valores brutos no lineales.

Paso 3. Determinar los límites del rango de ajuste de la turbina de vapor.

1. Cálculos

Para calcular el rango de ajuste, utilizaremos otro "bien de la civilización" : el método de casco convexo, casco convexo.

En MATLAB, esto se hace de la siguiente manera.

 indexCH = convhull(N, Qm, Ql, 'simplify', true); index = unique(indexCH); regRange = [N(index) Qm(index) Ql(index)]; regRangeQ0 = [regRange ones(size(regRange,1),1)] * A; fprintf('     = %d\n\n', size(index,1)); 

El método convhull () determina los puntos límite del rango de ajuste dados por los valores de las variables N, Qm, Ql. La variable indexCH contiene los vértices de los triángulos construidos usando la triangulación de Delaunay. La variable regRange contiene los puntos límite del rango de ajuste; variable regRangeQ0: caudales de vapor a alta presión para los puntos límite del rango de control.

El resultado del cálculo se puede encontrar en el archivo PT_80_linear_characteristic_curve.xlsx, hoja "PT-80-result", tabla "Límites del rango de ajuste".

Flujo linealizado característico construido. Es una fórmula (4) y 37 puntos que definen los límites (shell) del rango de ajuste en la tabla correspondiente.

2. Verificación

Al automatizar los procesos de cálculo, Q ₀ es necesario verificar si algún punto con los valores de N, Q _p , Q _{t está} dentro del rango de ajuste o fuera de él (el modo no es técnicamente factible). En MATLAB, esto se puede hacer de la siguiente manera.

Establecemos los valores de N, Q _p , Q _t que queremos verificar.

 n = 75; qm = 120; ql = 50; 

Lo comprobamos

 in1 = inpolygon(n, qm, regRange(:,1),regRange(:,2)); in2 = inpolygon(qm, ql, regRange(:,2),regRange(:,3)); in = in1 && in2; if in fprintf(' N = %3.2f , Q = %3.2f , Q = %3.2f     \n', n, qm, ql); else fprintf(' N = %3.2f , Q = %3.2f , Q = %3.2f      ( )\n', n, qm, ql); end 

La verificación se lleva a cabo en dos pasos:

• la variable in1 indica si los valores de N, Q _p han caído en la proyección del caparazón en el eje N, Q _p ;
• de manera similar, la variable in2 muestra si Q _p , Q _{t están} dentro de la proyección del caparazón en el eje de Q _p , Q _t .

Si ambas variables son iguales a 1 (verdadero), entonces el punto deseado está dentro de la carcasa, que establece el rango de ajuste de la turbina de vapor.

Ilustración del flujo linealizado obtenido, característico de una turbina de vapor.

Los "beneficios más generosos de la civilización" los obtuvimos en términos de ilustrar los resultados de los cálculos.

Primero, debemos decir que el espacio en el que construimos los gráficos, es decir, el espacio con los ejes x - N, y - Q _t , z - Q ₀ , w - Q _p , se denomina espacio de régimen (consulte Optimización del funcionamiento de las centrales térmicas en las condiciones mercado mayorista de electricidad y capacidad de Rusia

) Cada punto de este espacio define un cierto modo de funcionamiento de una turbina de vapor. El modo puede ser

• técnicamente factible, si el punto está dentro del caparazón que define el rango de ajuste,
• técnicamente no es factible si el punto está fuera de este caparazón.

Si hablamos del modo de operación de condensación de una turbina de vapor (Q _p = 0, Q _t = 0), entonces la característica de flujo linealizado es un segmento de línea recta . Si hablamos de una turbina de tipo T, entonces la característica de flujo linealizado es un polígono plano en un espacio de régimen tridimensional con los ejes x - N, y - Q _t , z - Q ₀ , que es fácil de visualizar. Para una turbina de tipo PT, la visualización es la más difícil, ya que la característica de flujo linealizado de dicha turbina es un polígono plano en un espacio de cuatro dimensiones (para explicaciones y ejemplos, consulte Optimización del funcionamiento de las centrales térmicas en el mercado mayorista de electricidad y energía de Rusia, sección Linealización de la característica de flujo de la turbina ).

1. Ilustración de las características de flujo linealizado obtenidas de una turbina de vapor

Construyamos los valores de la tabla "Datos de entrada (unidad de potencia)" en el espacio de régimen.

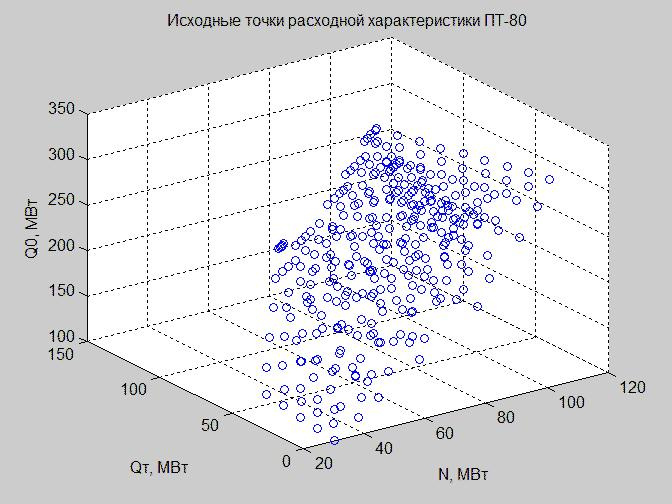
Fig. 3. Los puntos de partida de las características de flujo en el espacio de régimen con los ejes x - N, y - Q _t , z - Q ₀

Como no podemos construir dependencia en el espacio de cuatro dimensiones, todavía no hemos alcanzado una civilización tan buena, operamos con los valores de Q _{n de la} siguiente manera: excluirlos (Fig. 3), arreglar (Fig. 4) (ver el código para construir gráficos en MATLAB).

Fijamos el valor de Q _p = 40 MW y construimos los puntos de partida y la característica de flujo linealizado.

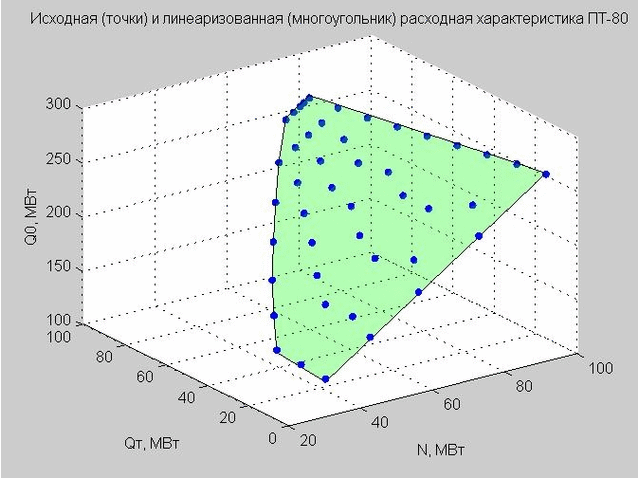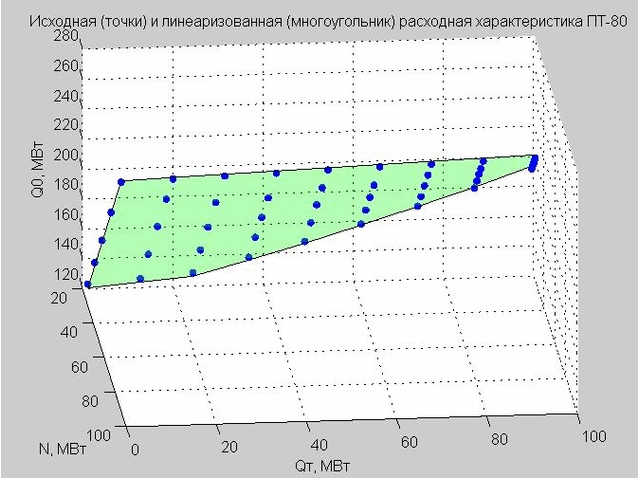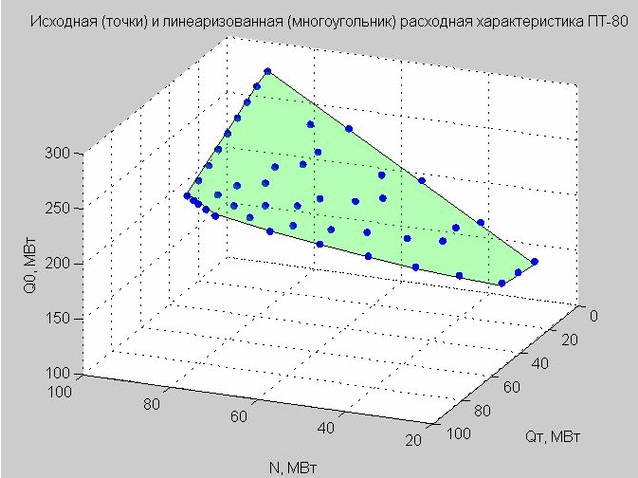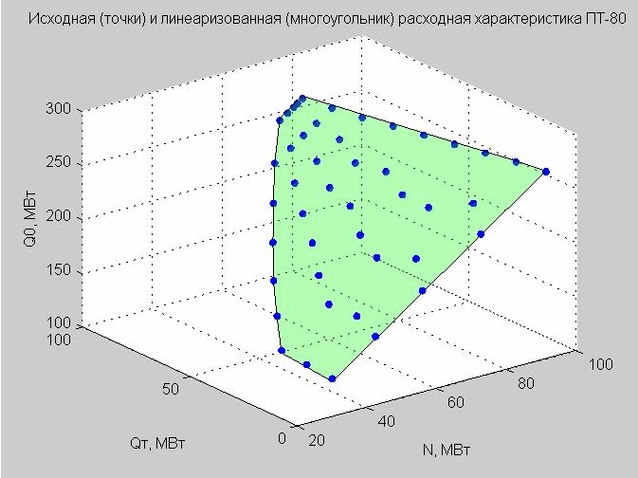
Fig. 4. Puntos de partida de la característica de descarga (puntos azules), característica de descarga linealizada (polígono plano verde)

Volvamos a la fórmula de la característica de flujo linealizado (4) que obtuvimos. Si arreglamos Q _p = 40 MW MW, entonces la fórmula tendrá la forma

$$$$ display $$ \ begin {ecation} Q_0 = 2.317 \ cdot N + 0.255 \ cdot Q_T + 58.714 \ qquad (6) \ end {ecation} $$ display $$

Este modelo define un polígono plano en un espacio tridimensional con los ejes x - N, y - Q _t , z - Q _0, por analogía con una turbina de tipo T (lo vemos en la Fig. 4).

Hace muchos años, cuando se desarrollaron nomogramas brutos q, se cometió un error fundamental en la etapa de análisis de los datos iniciales. En lugar de aplicar el método de mínimos cuadrados y construir una característica de flujo linealizado de una turbina de vapor por una razón desconocida, hicieron un cálculo primitivo:

$$$$ display $$ \ begin {ecation} Q_0 (N) = Q_ = Q_0 - Q_ - Q_ \ qquad (7) \ end {ecation} $$ display $$

Restado del caudal de vapor a alta presión Q _{0, el} caudal de los vapores Q _t , Q _py atribuye la diferencia resultante Q ₀ (N) = Q _e a la generación de electricidad. El valor obtenido Q ₀ (N) = Q _{e fue} dividido por N y convertido a kcal / kW · h, habiendo recibido un consumo específico q _t bruto. Este cálculo no cumple con las leyes de la termodinámica.

Queridos lectores, ¿quizás conozcan la razón desconocida? Compártelo!

2. Ilustración del rango de ajuste de la turbina de vapor.

Veamos el caparazón del rango de ajuste en el espacio del régimen. Los puntos de partida para su construcción se presentan en la Fig. 5. Estos son los mismos puntos que vemos en la fig. 3, sin embargo, el parámetro Q ₀ ahora _está excluido.

Fig. 5. Los puntos de partida de las características de flujo en el espacio de régimen con los ejes x - N, y - Q _p , z - Q _t

Muchos puntos en la fig. 5 es convexo. Usando la función convexhull (), definimos los puntos que definen la capa externa de este conjunto.

La triangulación de Delaunay (un conjunto de triángulos conectados) nos permite construir el caparazón del rango de ajuste. Los vértices de los triángulos son los valores límite del rango de ajuste de la turbina de vapor PT-80 en consideración.

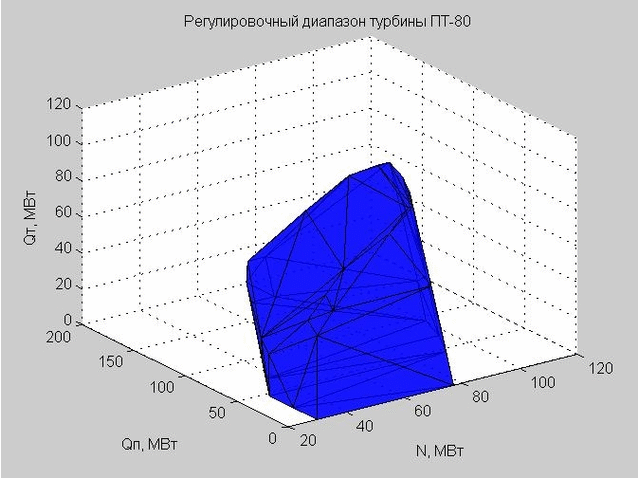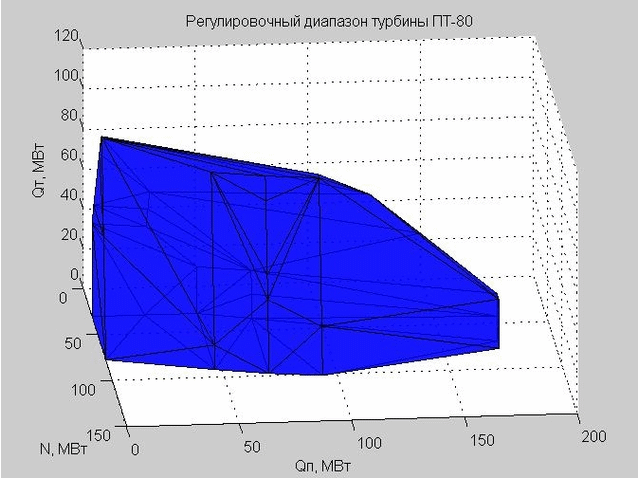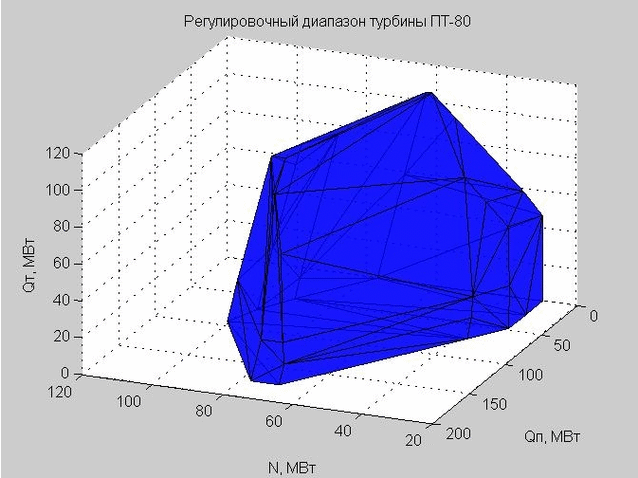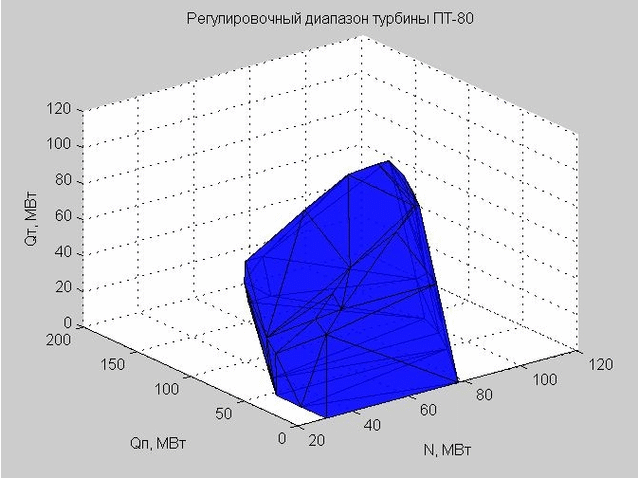
Fig. 6. El caparazón del rango de ajuste, representado por muchos triángulos.

Cuando verificamos un cierto punto para entrar dentro del rango de ajuste, verificamos si este punto se encuentra dentro o fuera del caparazón resultante.

Todos los gráficos presentados anteriormente se crean utilizando las herramientas de MATLAB (ver PT_80_linear_characteristic_curve.m).

Tareas prometedoras relacionadas con el análisis del funcionamiento de una turbina de vapor utilizando una característica de flujo linealizado.

Si está haciendo un diploma o una disertación, puedo ofrecerle varias tareas, cuya novedad científica puede demostrar fácilmente al mundo entero. Además, harás un trabajo excelente y útil.

Tarea 1

Muestre cómo cambia el polígono plano cuando cambia la presión de vapor de baja presión Q _t .

Tarea 2

Muestre cómo cambia el polígono plano cuando cambia la presión en el condensador.

Tarea 3

Compruebe si los coeficientes de la característica de flujo linealizado pueden representarse como funciones de parámetros adicionales del régimen, a saber:

$$$$ display $$ \ begin {ecation} \ alpha_N = f (p_ {0}, ...); \\ \ alpha_P = f (p_ {P}, ...); \\ \ alpha_T = f (p_ {T}, ...); \\ \ alpha_0 = f (p_ {2}, ...). \ end {ecuación} $$ display $$

Aquí p ₀ es la presión de vapor de alta presión, p _p es la presión de vapor de presión media, p _t es la presión de vapor de baja presión, p ₂ es la presión de vapor de escape en el condensador, todas las unidades son kgf / cm2.

Justifica el resultado.

Referencias

Chuchueva I.A., Inkina N.E. Optimización del CHP en las condiciones del mercado mayorista de energía eléctrica y capacidad de Rusia // Ciencia y Educación: Edición científica de MSTU. N.E. Bauman 2015. No. 8. S. 195-238.

• Sección 1. Declaración sustantiva del problema de optimizar el funcionamiento del CHP en Rusia
  
• Sección 2. Linealización del flujo característico de la turbina.
  
• Sección 3. Declaración formal del problema de la optimización a corto plazo de la operación de CHPP en una industria de energía eléctrica de mercado.
  
• Sección 4. Experimento Computacional
  
• Referencias con comentarios
  
• Comparación de las tareas de optimización 1 y 2 para determinar la composición óptima del equipo incluido.

Chuchueva I.A. Métodos computacionales para determinar el consumo específico de combustible equivalente de las centrales térmicas para la energía eléctrica y térmica suministrada en el modo de generación combinada // Ciencia y educación: publicación científica de MSTU. N.E. Bauman 2016. No. 2. P. 135-165.

• Sección 1. Declaración del problema.
  
• Sección 2. Descripción general del método
  
• Sección 3. Un nuevo método para calcular el consumo específico de combustible equivalente
  
• Sección 4. Comparación de métodos
  
• Referencias
  

Flujo linealizado característico de una turbina de vapor.

• Parte 1. Cuestiones clave
  
• Parte 2. Ejemplo de construcción para la turbina PT-80 en MATLAB
  
• Parte 3. Disipando mitos sobre los modos de funcionamiento de las turbinas de vapor