Masa, energía, impulso y la ley de conservación.

Muchas propiedades oscuras del mundo están asociadas con la naturaleza de la masa y la energía (así como el impulso). Todos escuchamos estas palabras, y muchos de nosotros tenemos una vaga idea de su significado. Por supuesto, los significados de las palabras "masa" y "energía" en inglés y otros idiomas son muchos. Desafortunadamente, ninguno de ellos coincide con los que los físicos tienen en mente. Intente dejar de lado estos significados de palabras y trabaje con conceptos físicos exactos; de lo contrario, estará completamente confundido.

Cabe señalar que no se debe recordar otro par popular, "sustancia y energía" con la frase "masa y energía". Muchas personas mencionan la última frase como si la materia y la energía fueran dos caras de la misma moneda. Pero esto no es así. La materia y la energía se dividen en diferentes categorías, como las manzanas y los orangutanes. Una sustancia, no importa cómo definirla, es una clase de objetos existentes en el Universo, y la masa y la energía no son objetos, sino las propiedades que poseen estos objetos. La masa y la energía están profundamente entrelazadas entre sí y merecen una explicación general.

Para comprender la masa y la energía, debe agregarles impulso y discutir las diferencias y relaciones de estas cantidades.

Energía

La palabra "energía" tiene muchos significados. Cuando nos enfermamos, decimos que no nos queda energía, refiriéndonos a la fuerza y ​​la motivación. Cuando decimos que alguien está lleno de energía, nos referimos a su gran actividad. Nos quejamos del aumento de los precios de la energía, en referencia al combustible. Estamos hablando de la energía espiritual como algo inconmensurable, pero importante, tal vez alguna forma de carisma. Y todos estos conceptos se superponen entre sí, por lo que elegimos una palabra para describirlos. Pero en física, la energía es una cosa completamente diferente. Desde el punto de vista de la física, una de estas definiciones se confundirá erróneamente con la física. En física, uno debe adherirse a un término físico para no obtener las respuestas incorrectas y no confundirse por completo.

Desafortunadamente, el concepto de "energía" en física es muy difícil de describir como lo hacen los diccionarios, con una frase breve y significativa. Pero no piense mal: todo es la imperfección del lenguaje natural, y no es que el concepto de energía en la física sea vago. En cualquier sistema físico dado, está completamente claro cuál es su energía, tanto en el sentido de su medición experimental como en el sentido de los cálculos (si hay ecuaciones que describen el sistema).

Una de las razones por las que la energía es tan difícil de describir es que puede tomar muchas formas y no todas son fáciles de entender. Aquí hay tres variedades comunes:

1. La energía puede estar encerrada en la masa de un objeto. Aquí llamo a esta opción "energía de masa" (gracias a la conocida ecuación E = mc ^{2, la} energía se une a la masa. También se llama "energía de reposo", ya que esta es la energía de un objeto en reposo, es decir, sin movimiento).

2. En segundo lugar, la energía está asociada con el movimiento de un objeto. Aquí lo llamo "energía de movimiento", y el término técnico para esto es energía cinética. Esta opción es intuitivamente fácil de entender, porque los objetos que se mueven rápidamente tienen más energía que los que se mueven lentamente. Además, un objeto pesado tiene más energía de movimiento que un objeto ligero que se mueve a la misma velocidad.

3. La energía puede almacenarse en la relación de objetos (y generalmente se denomina "potencial"). Se almacena en una fuente estirada, en el agua detrás de la presa, en la interacción gravitacional de la Tierra y el Sol, en las interacciones de los átomos en la molécula. Hay muchas formas de almacenar energía. Suena vago, pero el lenguaje tiene la culpa. En cualquiera de estos casos, existen fórmulas exactas que describen la energía almacenada en el sistema y formas bien definidas de medirlo.

El tercer tipo de energía está conectado con lo que llamaré la energía de interacción, y este es el concepto más confuso de todos. A diferencia de la energía de masa y la energía de movimiento, que siempre son mayores o iguales a cero, la energía de las interacciones puede ser positiva y negativa. Hasta ahora dejaré este tema, pero volveremos a él.

La energía es una cantidad especial de gran importancia para la física. La razón de esta importancia es que está "preservada". ¿Qué significa esto?

Si comienza la observación con un objeto o con un conjunto de objetos, los llamaremos un "sistema de objetos", que posee una cierta cantidad de energía en el momento inicial (no olvide calcular toda la energía: masas, movimientos, energía almacenada de todo tipo, etc.), y luego partes del sistema interactuarán solo entre sí y con nada más, luego, al final de la observación, la cantidad total de energía que poseen estos objetos será la misma que al principio. La energía total del sistema se conserva; su cantidad total no cambia. Puede cambiar de forma, pero si realiza un seguimiento de todas las variedades, al final será tanto como al principio.

Esta regla funciona incluso si algunos objetos desaparecen y dan paso a otros, por ejemplo, si una partícula en el sistema se descompone en otras dos fusionándose en el sistema.

¿Por qué se ahorra energía? Debido al principio matemático, correlaciona el hecho de que las leyes de la naturaleza no cambian con el tiempo, con la existencia de una cantidad conservada, que por definición llamamos "energía".

Le debemos la definición más famosa y general de este principio a Emmy Noether , uno de los más grandes físicos matemáticos del siglo anterior, contemporáneo de Einstein. Algunos miembros de la comunidad física y matemática la trataron con profundo respeto , pero en ese momento en su Alemania natal sufrió discriminación por motivos de género y nacionalidad (allí bloquearon los intentos de asignarle el título de profesora en Gotinga , y de allí tuvo que huir después de los nazis llegaron al poder). Después de emigrar a los Estados Unidos, después de solo dos años de enseñar en el Brin-Mar College (que hasta el día de hoy solo acepta mujeres para entrenamiento), murió de cáncer.

El famoso teorema de Noether (en realidad estos son dos teoremas estrechamente relacionados) nos dice que si hay simetría en las leyes de la naturaleza, en nuestro caso, esto significa que las leyes de la naturaleza son las mismas en cualquier momento, esto implica la conservación de una cierta cantidad, en nuestro caso, energía .

Además, el teorema nos dice exactamente cuál es la magnitud: cuáles son las diferentes formas de energía para un sistema dado de objetos que deben agregarse para obtener energía total. Es por eso que los físicos siempre saben exactamente qué es la energía, y por qué es más fácil obtener ecuaciones que definirlas con palabras.

Impulso

La situación con el impulso es aproximadamente la misma que con la energía. Las leyes de la naturaleza son las mismas en todas partes. Hablando en términos generales, los experimentos dan las mismas respuestas, ya sea que los pase al norte o al sur de aquí, al oeste o al este, en la parte superior de un edificio o en un pozo profundo. Elige cualquier dirección en el espacio. Entonces, según Noether, se conserva el impulso a lo largo de esta dirección. Dado que hay tres dimensiones en el espacio, es posible moverse en tres direcciones independientes diferentes y hay tres leyes de conservación independientes. Puede elegir cualquiera de las tres direcciones, siempre que sean diferentes. Por ejemplo, puede elegir pulsos en las direcciones norte-sur, oeste-este y arriba-abajo como las tres leyes de conservación. O puede elegir otros tres: en la dirección hacia y desde el Sol, a lo largo de la órbita de la Tierra en ambas direcciones, y hacia arriba y hacia abajo en relación con el plano del Sistema Solar. Su elección no importa, porque el impulso se almacena en cualquier dirección.

La forma más simple de impulso surge debido al simple movimiento de los objetos, y esto es algo que se puede imaginar intuitivamente: si un objeto se mueve en una dirección determinada, entonces tiene un impulso en esa dirección, y cuanto más rápido se mueva, mayor será este impulso. Y un objeto más pesado tiene un mayor impulso que uno ligero si se mueven a la misma velocidad.

Una de las consecuencias interesantes de esta conservación: si tiene un sistema de objetos inmóvil (es decir, el sistema en su conjunto no se mueve si promedia todos los movimientos de sus objetos constitutivos), entonces permanecerá inmóvil, a menos que reciba un movimiento externo. impacto La razón es que en un sistema fijo, el impulso total es cero, y dado que se mantiene el impulso, seguirá siendo cero para siempre a menos que algo intervenga desde fuera del sistema.

Masa y su relación con la energía y el impulso.

Ahora pasemos a la masa

Desafortunadamente, hay mucha confusión asociada con la masa: después de la publicación del trabajo de Einstein sobre la teoría de la relatividad, durante algún tiempo hubo dos conceptos de masa. Y solo uno de ellos (aquel en el que se detuvo el propio Einstein, y que a veces se llama la "masa invariante" o "masa en reposo" para distinguirlo del término ya arcaico "masa relativista"), todavía se usa en física de partículas. En otro artículo explicaré esto con más detalle.


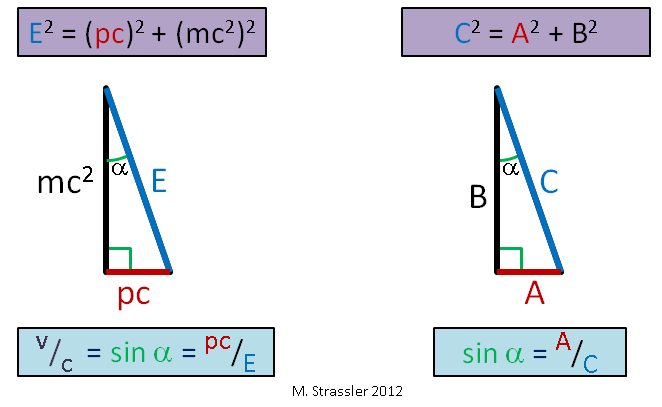Fig. 1

Por masa m, que uso en artículos, se entiende esa masa que une directamente la energía y el impulso. Para un objeto que se mueve sin la influencia de fuerzas externas (que no interactúan significativamente con otros objetos), Einstein sugirió (y esto fue confirmado por experimentos) que su energía E, momento p y masa m satisfacen la simple igualdad de Pitágoras:

$$ $$E ^ 2 = (p c) ^ 2 + (mc ^ 2) ^ 2 \ qquad (ecuación No. 1)$$

Recuerda al viejo Pitágoras que afirmó que para un triángulo rectángulo con lados A y B e hipotenusa C, la igualdad $$$C ^ 2 = A ^ 2 + B ^ 2$ ? Esta es una conexión del mismo tipo - ver fig. 1. Con nosotros, c es una velocidad constante que, como veremos, sirve como límite de velocidad universal. También veremos por qué se llama la "velocidad de la luz".

Según las ecuaciones de Einstein, la velocidad de un objeto dividido por el límite de velocidad c es solo la relación de pc a E:

$$ $$v / c = (p c) / E \ qquad (ecuación # 2)$$

Es decir, la relación de la pierna horizontal a la hipotenusa. También es igual al seno del ángulo α en la Fig. 1. Entonces aquí, ciudadanos. Y dado que las patas de un triángulo rectángulo siempre son más cortas que la hipotenusa (el seno de cualquier ángulo siempre es menor o igual a 1), la velocidad de cualquier objeto no puede exceder s, el límite de velocidad universal. Con un aumento en la velocidad de un objeto de una masa fija, py E se vuelven muy grandes (Fig. 2), pero E siempre es mayor que pc, entonces v siempre es menor que c!


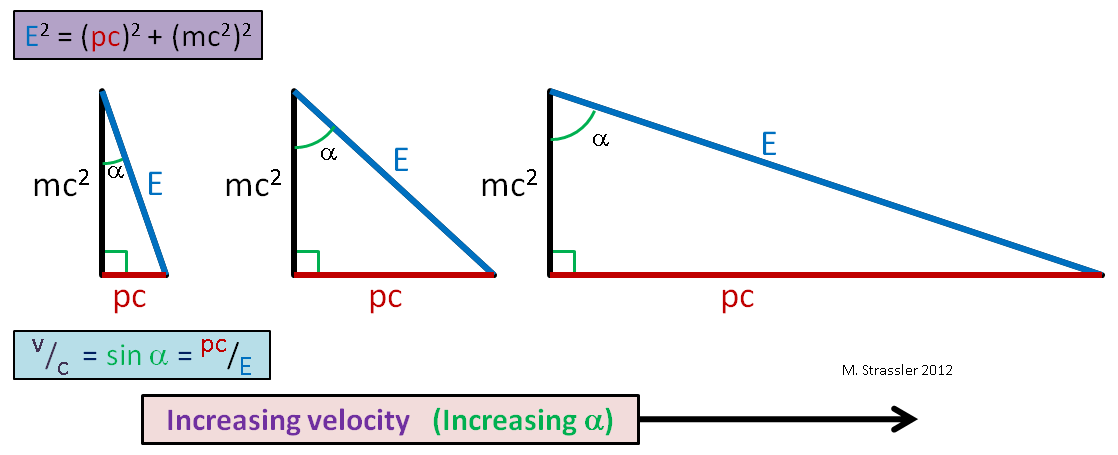Fig. 2

Ahora tenga en cuenta que si el objeto no se mueve, entonces su impulso p es igual a cero, y la relación en la ecuación 1 se reduce a:

$$ $$E ^ 2 = (mc ^ 2) ^ 2, \ quad o \ quad E = mc ^ 2$$

La famosa fórmula de Einstein, la relación de la masa con una cantidad fija de energía (lo que yo llamo energía de masa), es simplemente una declaración correspondiente al hecho de que cuando un triángulo se degenera en una línea vertical, como en la Fig. 3 a la izquierda, su hipotenusa se convierte en la misma longitud que la pierna vertical. Al mismo tiempo, no significa que la energía siempre sea igual a la masa por el cuadrado s. Esto solo funciona para un objeto en reposo con momento cero.


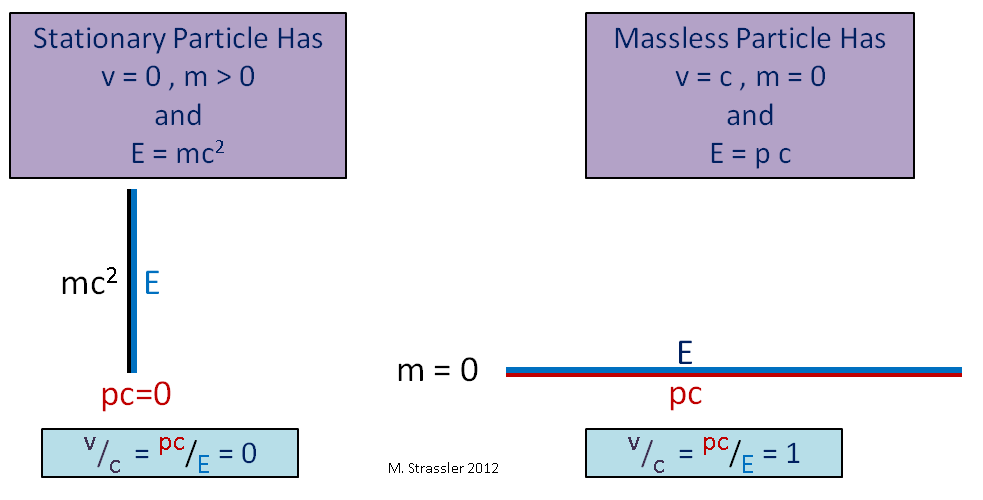Fig. 3

Otra observación interesante: para una partícula sin masa, la pata vertical del triángulo es cero, y la hipotenusa y la pata horizontal son iguales, como en la Fig. 3. En este caso, E es pc, lo que significa que v / c = 1, o v = c. Se ve que una partícula sin masa (por ejemplo, un fotón, una partícula de luz) se mueve inevitablemente a una velocidad de c. Por lo tanto, la velocidad de la luz es la misma que el límite de velocidad universal, s.

Por otro lado, si tomamos una partícula con masa, como en la Fig. 4, no importa cuán grande sea el impulso y la energía, E siempre será un poco más que p * c, por lo que la velocidad siempre será menor que s. Las partículas sin masa deben viajar a la velocidad máxima. La velocidad de las partículas masivas debería ser menor.


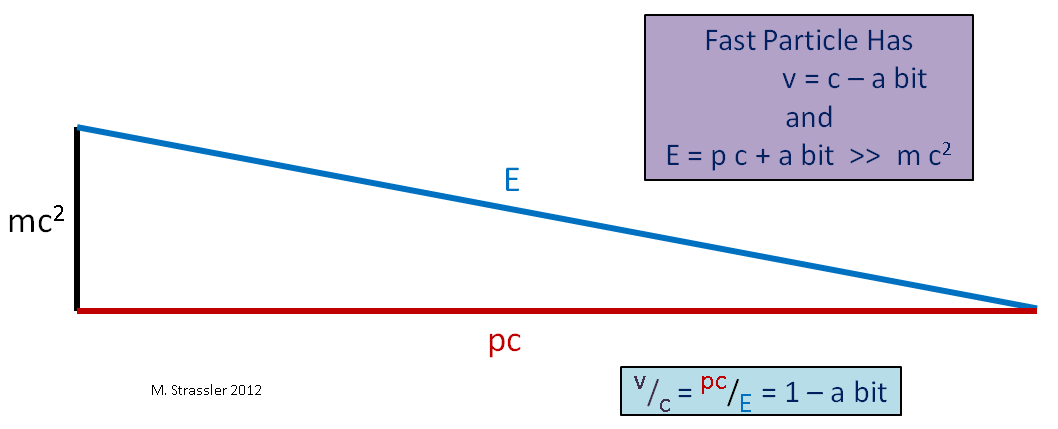Fig. 4. Aquí ">>" significa "mucho más"

Imagine otro caso límite, un objeto masivo que se mueve lentamente (en comparación con la velocidad de la luz), como un automóvil. Como su velocidad v es mucho menor que c, su impulso p veces c será mucho menor que E y, como se puede ver en la Fig. 5, E será un poco más que mc ² . Por lo tanto, la energía de movimiento de un objeto lento E - mc ^{2 es} mucho menor que la energía de su masa mc ² , y para un objeto rápido la energía de movimiento puede hacerse arbitrariamente grande, como vimos en la Fig. 4)

Un punto sutil: el impulso no es solo un número, sino también un vector. Él tiene magnitud y dirección. Está dirigido hacia el movimiento de la partícula. Cuando escribo p, solo indico el valor. En muchos casos, es necesario seguir la dirección del pulso, aunque en la ecuación No. 1, que relaciona el pulso con la energía y la masa, esto no es necesario.


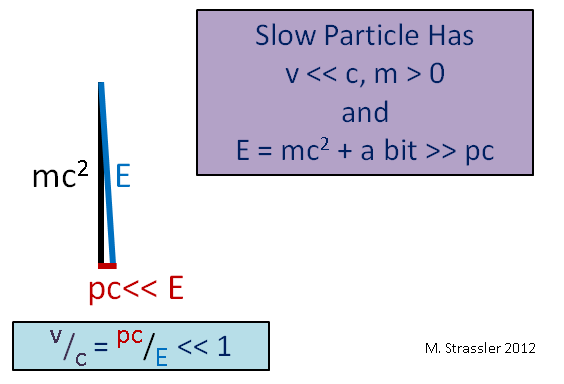Fig. 5 5

Otro punto sutil: utilicé triángulos y trigonometría simple, ya que es conocido por todos desde la escuela. Los expertos deben ser más cuidadosos: puede comprender correctamente las ecuaciones de Einstein utilizando funciones hiperbólicas que generalmente no encuentran los aficionados, pero que son extremadamente importantes para comprender la estructura de la teoría y hacer que las cosas sean más comprensibles, como la adición de velocidad, la compresión de distancia, etc. Las personas que no pretenden ser expertos pueden ignorar esto.

Pero es la velocidad relativa? ..

Si lees cuidadosamente el texto, algo ya puede sorprenderte. Sabes que la velocidad de una partícula, o cualquier cosa que se mueva más lentamente que la luz, depende del punto de vista.

Si te sientas en casa y lees un libro, dirás que la velocidad del libro es cero (y realmente descansa en relación a ti), por lo tanto, no tiene impulso ni energía de movimiento, solo energía de masa. Pero si me parara en la luna, te recordaría que la Tierra está girando, por lo que esta rotación te cautiva y te mueve en relación a mí a una velocidad de cientos de kilómetros por hora. Entonces, usted y su libro tendrían el impulso desde mi punto de vista.

¿Quién tiene la razón?

La variante de la relatividad según Galileo, el primer principio de la relatividad, afirma que ambos tenemos razón. La variante de relatividad de Einstein está de acuerdo con el punto de vista de Galileo de que ambos tienen razón, pero hace ajustes importantes en cómo los seguidores de Galileo indicarían la energía, el momento y la masa del libro, colocando estas cantidades en la relación pitagórica de la ecuación No. 1.

Pero si todo está bien, qué E y qué p necesito sustituir en la relación de energía / momento / masa, $$$E ^ 2 = (p c) ^ 2 + (mc ^ 2) ^ 2$ ? Sustituya E y p medidos leyendo el libro, es decir, E = mc ² y p = 0? ¿O sustituir E y p, que el libro tiene desde mi punto de vista, cuando te mueves con la Tierra?

La respuesta a esta pregunta contiene toda la esencia de la ecuación n. ° 1 de Einstein. Cada observador medirá diferentes valores de E y p para el libro, dependiendo de qué tan rápido se mueva el libro con respecto a él. Pero para todos los observadores la ecuación $$$E ^ 2 = (p c) ^ 2 + (mc ^ 2) ^ 2$ será verdad!

La magia! Pero, de hecho, el genio es una idea que surgió en 1905 sobre cómo reemplazar el conjunto de ecuaciones propuestas por Newton y sus seguidores con un nuevo y sorprendente conjunto de ecuaciones, que todavía coincide con todos los experimentos anteriores, pero resultó ser una representación más precisa de la realidad. Es difícil imaginar cuánto fue necesario cambiar la forma de pensar para pensar en ello hasta que descubra cuánto podría salir mal durante la formación de la nueva teoría, y cuántas otras ecuaciones diferentes que contienen contradicciones con las matemáticas o con experimentos anteriores, puede Sería ofrecer (y la gente los ofreció). Por ejemplo, el trabajo de los físicos novatos viene constantemente a mí, tratando de "arreglar" las ecuaciones de Einstein, pero nunca he visto a ninguno de ellos verificar la consistencia interna de sus ecuaciones. Esta es una tarea muy difícil y la razón del fracaso de la mayoría de las teorías.

Pero, ¿cómo se puede conservar la energía y el impulso?

Espera un minuto, dices, cuando tu cabeza esté lista para explotar y salpicar todo a tu alrededor con tu cerebro (recuerdo esta sensación yo mismo), ¡pero debes conservar la energía y el impulso! Entonces, ¿cómo pueden los diferentes observadores estar en desacuerdo con lo que son?

Hay incluso más magia, que, por cierto, fue anterior a Einstein. Créame, el Universo es un contador muy, muy inteligente, y a pesar del hecho de que diferentes observadores no estarán de acuerdo con la energía disponible en un objeto o sistema de objetos, todos estarán de acuerdo en que esta energía no cambia con el tiempo. Lo mismo vale para el impulso.

Pero la masa es muy diferente de la energía y el impulso. Primero, la masa no se conserva. En la naturaleza, hay muchos procesos que cambian la masa total de un sistema: por ejemplo, una partícula de Higgs masiva puede descomponerse en dos fotones sin masa. No hay simetría asociada con la masa y, por lo tanto, Noether no tiene ninguna ley de conservación para nosotros. En segundo lugar, a diferencia de la energía y el impulso, cuyos valores dependen del observador (en particular, de su velocidad en relación con los objetos medidos), todos los observadores estarán de acuerdo con la masa m del objeto. Y esto no es del todo obvio, y sucede porque las ecuaciones de Einstein funcionan terriblemente astutamente.

Entonces que tenemos

Por el momento, tenemos varios, a primera vista, conocimientos contradictorios. Sabemos que:

• La energía y el momento de un sistema físico aislado se conservan (la energía total y el momento total de un sistema aislado no cambian con el tiempo) desde el punto de vista de cualquier observador.
• ¡Los diferentes observadores que se mueven entre sí evaluarán los valores de la energía y el impulso del sistema de manera diferente!
• La suma de las masas de los objetos que componen el sistema no se guarda, puede cambiar.
• Pero todos los observadores estarán de acuerdo con la masa del objeto.

Se deben agregar dos hechos más y dos conclusiones a esta lista:

la masa del sistema físico de objetos no es igual a la suma de las masas de los objetos que componen este sistema.

En cambio, la masa del sistema físico, sobre la cual todos los observadores están de acuerdo, está determinada por su energía e impulso, y satisface su versión de la ecuación No. 1:

$$ $$(E_{system})^2 = (p_{system} c)^2 + (m_{system} c^2)^2 \qquad ( №1')$$

Resulta que no se necesita una ley de conservación adicional, y que aunque la suma de las masas de los objetos que componen el sistema no se conserva, la masa del sistema se conserva, ya que está conectada a través de la ecuación No. 1 'a la energía y el momento del sistema que se almacenan.

La masa del sistema de objetos es el único elemento en nuestra lista que se conserva simultáneamente y no está sujeto a debate por parte de los observadores.

Solo necesita recordar que la masa del sistema de objetos no es la suma de las masas de los objetos que componen el sistema, sino lo que se da por la ecuación No. 1 '.

Luego trate de explicarlo, solo vea cómo funciona. Un ejemplo vívido vale más que mil palabras. Tomemos como ejemplo de un sistema lo más moderno, a saber, la partícula de Higgs (que tiene una masa de 126 GeV / s ² ), y vea cómo funcionan las diversas declaraciones anteriores cuando se descompone en dos fotones.

Una partícula de Higgs, dos fotones y tres observadores.

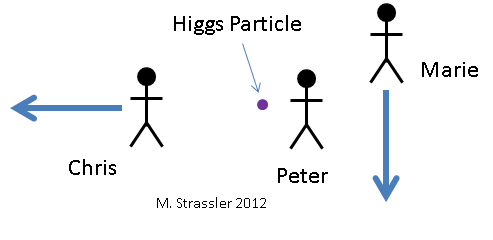Fig. 6. Tres observadores miran la partícula de Higgs. En relación con ella, Petya (Peter) no se mueve, Masha (Marie) se mueve hacia abajo y Kostya (Chris) se mueve hacia la izquierda.

Veamos cómo la partícula de Higgs se descompone en dos fotones, desde el punto de vista de tres observadores diferentes. Se muestran en la fig. 6 junto con la partícula de Higgs que están mirando. Por supuesto, no pueden verla a través de los ojos, porque existe muy poco tiempo y es demasiado pequeña. Necesitan usar algún tipo de equipo científico. Para Petit, la partícula de Higgs no se mueve. Masha se mueve hacia abajo en relación con Petit. Kostya se mueve a la izquierda en relación con Petit. Entonces, para Masha, la partícula de Higgs se mueve hacia arriba, y para Bone, a la derecha. Tres observadores ven cómo se descompone una partícula según la fig. 7. Petya ve que Higgs se descompone en dos fotones de la misma energía, uno de los cuales se mueve hacia arriba y el otro hacia abajo. Masha ve que Higgs se descompone en dos fotones de diferentes energías, y que una energía que se mueve hacia arriba tiene más energía que una que se mueve hacia abajo.Kostya ve que Higgs se descompone en dos fotones que se dirigen hacia arriba y hacia abajo. Calculemos qué energías y momentos son asignados a los Higgs y dos fotones por los observadores, y cómo cada uno de ellos llegará a la conclusión de que la energía y el momento se conservan durante la desintegración.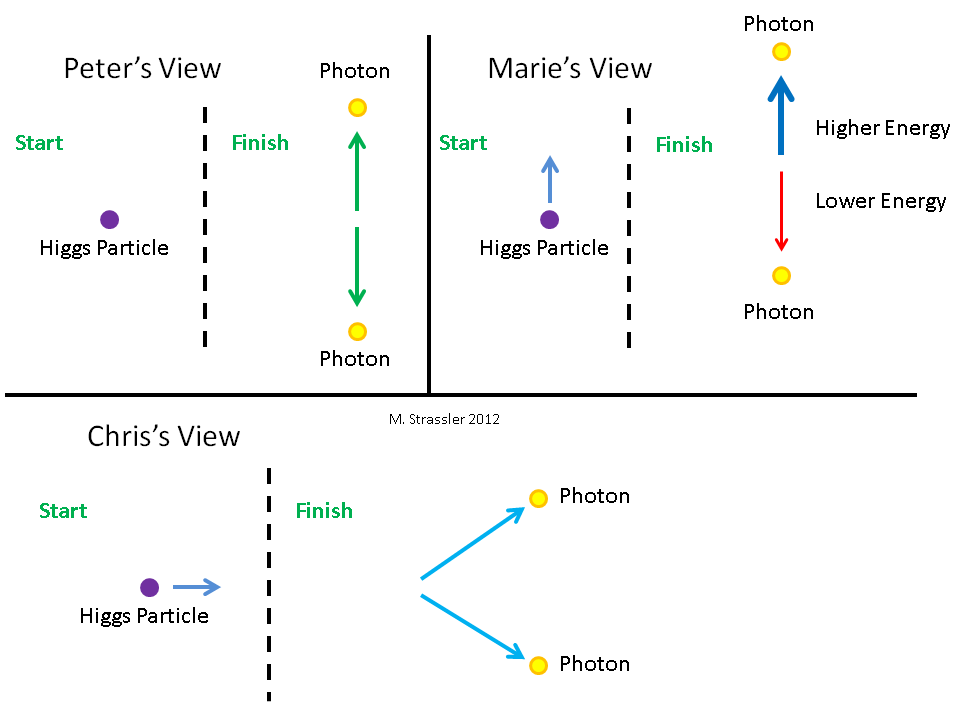

Descomposición de partículas de Higgs

Primero, analizamos la partícula de Higgs desde el punto de vista de Petit. Petya está mirando (usando instrumentos de medición) la partícula de Higgs, ¿y qué ve? (Pondré un trazo sobre todo lo que Petya ve, y luego comparamos esto con las observaciones de Masha y Kostya). Higgs no se mueve, por lo que su impulso$$$\overline{p_0}$es igual a cero, y de acuerdo con la ecuación No. 1 he, con su masa m = 126 GeV / c ^{2, la} energía será$$$\overline{E_0} = m c^2 = 126$

Ahora, de acuerdo con la conservación de la energía y el momento, un sistema que consiste en una partícula de Higgs conservará toda la energía y el momento después de la descomposición. Y esto será así hasta que ninguna fuerza externa afecte a Higgs. Puede preguntar si necesitamos preocuparnos por la gravedad, porque la gravedad será una influencia externa que puede cambiar el impulso. Mi respuesta es que en el corto tiempo que decae Higgs, el efecto de la gravedad será tan pequeño que si te dijera lo pequeño que es en realidad, te reirías. Olvídate de eso.

Entonces, cuando decae Higgs, las energías de las partículas que forman sus residuos deben sumar 126 GeV, y el impulso de las partículas (dado que el impulso no es solo una cantidad, sino también una dirección, un vector) totalizará cero.

Dos fotones sin masa en los que las desintegraciones de Higgs pueden dispersarse en cualquier dirección, pero para simplificar el ejemplo, imagine que se dispersan verticalmente, uno arriba y otro, rebotando hacia abajo. (Un poco más adelante discutiremos por qué deberían volar en direcciones opuestas).

¿Qué impulso tienen los fotones? Es simple En primer lugar, el impulso total del sistema, la suma de los momentos de dos fotones, debe ser cero, ya que Higgs tenía un impulso cero antes de la descomposición (desde el punto de vista de Petit). Ahora cada uno de los fotones tiene un impulso de cierta magnitud y dirección. En total, pueden dar cero de una sola manera, si son de igual magnitud y en la dirección opuesta. Si uno sube, el otro debería bajar, y su tamaño debería ser el mismo.


Fig. 8: lo que ve Petya

. En segundo lugar, la energía total del sistema es la suma de las energías de dos fotones. Esto se debe a que no hay energía de interacción entre ellos (a excepción de una atracción gravitacional extremadamente pequeña, de la que puede olvidarse). Por supuesto, dado que no tienen masas, toda su energía está en la energía del movimiento. Además, en el caso de una partícula sin masa, la ecuación No. 1 sugiere que E = pc, donde p es el momento. Debido a esto, dos fotones con el mismo momento deben tener la misma energía. Y dado que estas dos energías deberían sumarse a la energía de la partícula de Higgs, la energía de cada fotón debería ser igual a la mitad de la energía de la partícula de Higgs.

$$ $$\overline E_1 = \overline E_2 = 1/2 (126 ) = 63$$

Y dado que para una partícula sin masa p = E / c, entonces

$$ $$\overline p_1 = 63 /c \uparrow \\ \overline p_2 = 63 /c \downarrow$$

Y se muestra en la fig. 8)

La energía y el impulso se conservan, pero la masa no, porque los fotones no tienen masa, pero Higgs sí. ¿Qué pasa con la masa del sistema? ¿Cuál es la masa de un sistema de dos fotones? Distinto de cero Obviamente lo que ella es. De la misma manera que para el propio Higgs (del cual se compuso originalmente todo el sistema), un sistema de dos fotones tiene la misma energía e impulso que tenía Higgs:

$$ $$E_{system} = \overline E_1 + \overline E_2 = 63 + 63 = 126 \\ p_{system} = \overline p_1 \uparrow + \overline p_2 \downarrow = 63 /c \uparrow + 63 /c \downarrow = 0$$

Y desde Petit $$$p_{system} = 0$ ,

$$ $$m_{system} = E_{system} / c^2 = 126 /c^2$$

Esa es la masa de Higgs. La masa del sistema no cambió durante la descomposición, como se esperaba.

El observador por el que Higgs sube

Masha se mueve hacia abajo en relación con Peta, por lo que desde su punto de vista, Petya y Higgs se mueven hacia arriba. Suponga que Higgs se mueve a una velocidad de v = 0.8 s, es decir, 4/5 de la velocidad de la luz en relación con ella. A diferencia de Petya, desde el punto de vista de Masha, Higgs tiene un momento distinto de cero, y los momentos de los fotones son de diferente magnitud, pero aún multidireccionales, como resultado de lo cual la suma de sus momentos no será cero.


Fig. 9: cómo Masha ve la descomposición de la partícula de Higgs

¿Cómo calcular qué momento y energía tienen el Higgs y los dos fotones en los que se descompone, desde el punto de vista de Masha? Para hacer esto, necesitamos otro conjunto de ecuaciones simples de Einstein. Supongamos que, desde el punto de vista de cierto observador, el objeto tiene impulso p y energía E. Luego, desde el punto de vista de otro observador que se mueve con velocidad v en la dirección del objeto (o contra él), el impulso y la energía del objeto se expresarán de la siguiente manera:

$$ $$p = γ (\overline p+ v \overline E/c^2) \qquad ( №3) \\ E = γ (\overline E + v \overline p) \qquad ( №4)$$

Donde γ satisface otra ecuación pitagórica:

$$ $$1 = v^2/c^2 + 1/γ^2 \qquad ( №5)$$

según Einstein Esto nos permite llevar a cabo transformaciones entre lo que ve Petya y lo que ve Masha (o cualquier otro observador que se mueva con velocidad v). Lo que encontramos se muestra en la Fig. 9)

Para comparar las observaciones de Masha con las de Petya, necesitamos v y γ. Sostengo que si v = 4/5 c, entonces γ = 5/3.

Verifiquemos usando la ecuación No. 5: 1 = (4/5) 2 + (3/5) 2 = 16/25 + 9/25 = 25/25 Petia

dice que en Higgs$$$p_0=0, E_0=126$ .¿Qué hay de Masha? Ella dice que:

$$ $$p_0 = γ v \overline E_0 = (5/3) (4/5) \overline E_0 = 168 /c \uparrow \\ E_0 = γ \overline E_0 = (5/3) \overline E_0 = 210$$

Petya afirma que dos fotones $$$\overline E_1 = \overline E_2 = 63$, y para cada uno de ellos E = p c. Ahora podemos calcular lo que Masha ve usando las ecuaciones No. 4 y No. 4.

$$ $$E_1= γ (1+v) \overline E_1 = 189 , p_1 = E_1/c \uparrow$$

$$ $$E_2= γ (1-v) \overline E_2= 21 , p_2 =E_2/c \downarrow$$

Funciona! La energía también se conserva desde el punto de vista de Mary, porque

$$ $$E_0 = 210 \\ E_1 + E_2 = (189 + 21) = 210$$

Impulse también se guarda:

$$ $$p_0 = 168 /c \uparrow \\ p_1 + p_2 = 189 /c \uparrow + 21 /c \downarrow = (189 – 21) /c \uparrow = 168 /c \uparrow$$

La masa del sistema coincide con la masa de Higgs antes y después de la descomposición, ya que antes y después de la descomposición

$$ $$E_system = 210 \\ p_system = 168 /c \uparrow$$

Lo cual, según la ecuación No. 1 ', devuelve la masa del sistema a $$$126 /c^2$ como con Petit, porque

$$ $$210^2 = 168^2 + 126^2$$

El observador, desde el punto de vista de que Higgs se mueve hacia la derecha

¿Qué tenemos con Bones? Kostya se mueve hacia la izquierda en relación con Petya, por ejemplo, a una velocidad de v = 4/5 s, de modo que Higgs (y Petya) se mueven hacia la derecha con respecto a Kostya a una velocidad de v = 4/5 s. Los mismos cálculos que hicimos para Masha muestran que la energía de Higgs$$$E_0 = 210 GeV y p_0 = 168 GeV$ pero, a diferencia de Masha, para quien Higgs se mueve hacia arriba, para Kostya el impulso de Higgs se dirige hacia la derecha. Esto se muestra en la fig. 10)


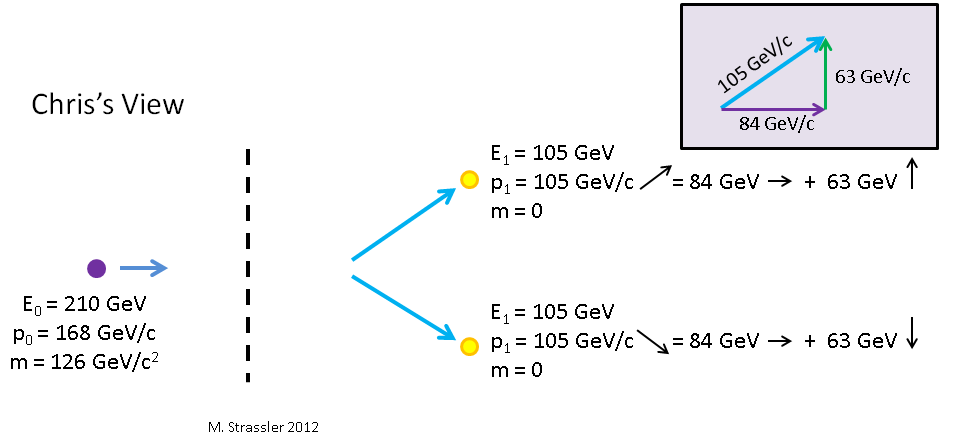
Fig. 10

Higgs se descompone en dos fotones. Si desde el punto de vista de Petya los fotones se mueven hacia arriba y hacia abajo, entonces para Kostya, que observa a Higgs y Petya moverse hacia la derecha, uno de los fotones se mueve hacia la derecha y el otro hacia la derecha. ¿Qué impulso y energía tendrán entonces?

A través de las ecuaciones No. 4 y No. 5 no lo sabemos, porque están destinadas a casos en que la partícula y el observador se mueven en la misma dirección. Para nuestro caso, las ecuaciones serán las siguientes:

$$ $$\ updownarrow p = \ updownarrow \ overline p \\ \ leftrightarrow p = γ ([\ leftrightarrow \ overline p] + v \ overline E / c ^ 2) \\ E = γ (\ overline E + v [\ leftrightarrow \ overline p])$$

Estas ecuaciones serán más simples de lo que parecen, ya que desde el punto de vista de Petit, p no tiene un componente que se mueva de izquierda a derecha, y todo el pulso sube o baja. Entonces Kostya observa los siguientes valores para Higgs:

$$ $$\ updownarrow p_0 = \ updownarrow \ overline p_0 = 0 \\ \ leftrightarrow p_0 = γ v \ overline {E_0} / c ^ 2 = (5/3) (4/5) 126 GeV / c = 168 GeV / c \ flecha derecha \\ E = γ \ overline {E_0} = (5/3) 126 GeV = 210 GeV$$

Y el fotón subiendo

$$ $$\ updownarrow p_0 = \ updownarrow \ overline p_1 = 63 GeV / c \ uparrow \\ \ leftrightarrow p_0 = γ v \ overline {E_1} = (5/3) (4/5) 63 GeV / c = 84 GeV / c \ rightarrow \\ E = γ \ overline {E_0} = (5/3) 63 GeV = 105 GeV$$

Para el segundo fotón, las fórmulas son las mismas, solo su componente vertical se dirige hacia abajo. Tenga en cuenta que para ambos fotones E = pc, de acuerdo con el teorema de Pitágoras para el tamaño p para cada uno de los pulsos, de acuerdo con el recuadro de la Fig. 10

$$ $$p_1 ^ 2 = (\ uparrow p_1) ^ 2 + (\ rightarrow p_1) ^ 2 \\ o \\ (105 GeV / c) ^ 2 = (63 GeV / c) ^ 2 + (84 GeV / c) ^ 2$$

Y de nuevo, Kostya observa otros valores de energía e impulso, en comparación con Petya y Masha. Pero para Kostya, la energía y el impulso aún se conservan. Kostya también observa que la masa de un sistema con dos fotones coincide con la masa de Higgs. Por qué La parte vertical total del impulso del sistema es cero, se destruye mutuamente. La parte horizontal del pulso del sistema es de 168 GeV / s. La energía total del sistema es de 210 GeV. Esto es lo mismo que observó Masha, excepto que su impulso del sistema aumentó, y no a la derecha. Pero la dirección del pulso no afecta la ecuación No. 1 '. Solo su magnitud juega un papel allí. Entonces, como Masha, Kostya ve que la masa del sistema de dos protones es $$$126 GeV / c ^ 2$ igual a la masa de la partícula primaria de Higgs.

Resumen

Entonces vemos lo que observan tres observadores diferentes. Sus observaciones:

• variar en cuanto a la energía de Higgs y el momento,
• variar en términos de energía y momento de ambos fotones,
• acordar la conservación de la energía y el impulso durante la descomposición,
• por lo tanto, están de acuerdo en que se preserva la masa del sistema,
• aceptar que la masa del sistema es 126 GeV / c ² ,
• y, además, que la suma de las masas de los objetos del sistema no se conserva, sino que disminuye de 126 GeV / c ² a cero.

Y esto no es casualidad. Einstein de experimentos anteriores sabía que la energía y el impulso se conservan, por lo que buscó y encontró ecuaciones que preservan esta característica del mundo. También en el proceso, descubrió que la masa del sistema debe satisfacer la ecuación No. 1 '.

Bono: cómo se usa en busca de una partícula de Higgs

Científicos:

• observar colisiones de protones, como resultado de las cuales nacen dos fotones;
• calcular la masa de un sistema de dos fotones (en la jerga técnica se llama masa invariante de un par de fotones).

Cuando, como resultado de un experimento, una partícula de Higgs se descompone en dos fotones, no importa en qué dirección y velocidad se mueva la partícula con respecto al laboratorio, el sistema de dos fotones en el que se descompone siempre tendrá una masa igual a la masa ¡Partículas de Higgs que las produjeron! Por lo tanto, a diferencia de los procesos aleatorios, que dan como resultado un sistema de dos fotones de masa aleatoria, las partículas de Higgs siempre generarán un sistema de dos fotones de la misma masa. Por lo tanto, si las partículas de Higgs aparecen en los resultados del experimento, y si a veces se descomponen en dos fotones, entonces veremos un pico de desintegraciones de Higgs que se eleva por encima del fondo liso de otros procesos aleatorios. ¡Y así sucedió en el experimento en el LHC!