El desafío para los niños de cinco años que se ha vuelto "viral"

Toda la verdad sobre el último rompecabezas de virus de Singapur y otro acertijo histórico con números



En honor al aniversario de esta columna, Internet me ha proporcionado amablemente un problema matemático de Singapur que se ha vuelto viral . A mediados de mayo, la web quedó encantada con la tarea que supuestamente resuelven los alumnos de primer grado de Singapur, que son niños de 5 a 7 años, y que resultó ser tan difícil que nadie puede resolverla.


Estudie cuidadosamente la secuencia de números y complete los espacios en blanco

Pero nuestra historia trata sobre cómo frases como "un problema matemático agitó Internet" se convirtieron en intentos aburridos y predecibles para atraer visitantes a la página. Dado que incluso un breve vistazo a este problema, que apareció por primera vez en el foro técnico de Singapur , nos permite decir que esta foto es una falsa obvia. La foto parece editada, pero no hay explicación para la tarea.

Aparentemente, el rompecabezas fue tomado (y modificado) de un sitio dedicado a los rompecabezas matemáticos, dirigido por Gordon Burgin, un maestro retirado estadounidense. Y en la versión del sitio en el cuarto inferior izquierdo está el número 20. En la foto de Singapur, 0 está manchado. ¡No es de extrañar que no haya una solución obvia!

"Estoy sorprendido por esta falsificación y no sé qué estaban tratando de lograr", dice Burgin. "Si su objetivo era una discusión acalorada y una desesperación posterior, ¡entonces lograron su objetivo!"

El siguiente es el acertijo correcto.

1. En cada uno de los cuatro sectores del círculo exterior hay un número de dos dígitos igual a la suma de los tres números ubicados en las esquinas de este sector. Los números en círculos individuales pueden variar del 1 al 9, y cada uno de los números se puede usar solo una vez. Se le da uno de los números para comenzar. Encuentra los cuatro restantes.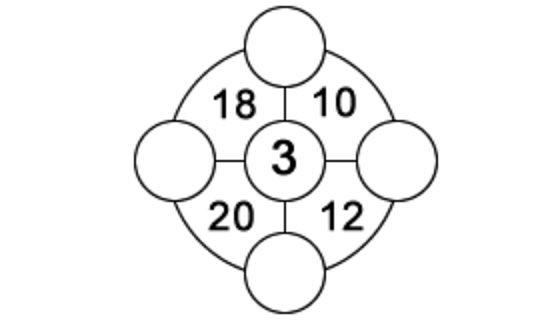



2. Dado que el acertijo de Singapur era incorrecto, intente proponer una variante del problema que sea adecuada para la imagen dada (con un cero).

Este acertijo me recordó a un rompecabezas de uno de los libros más interesantes sobre la historia de los acertijos: " Wakoku chiekurabe ", el libro de acertijos japonés más antiguo, publicado en 1727. Este es un misterio maravilloso, ¡y al menos acaba de nacer en el Este!

3. Escriba los números del 1 al 9 en círculos negros para que la suma de los números ubicados en cada uno de los dos círculos azules (incluido el círculo central), así como a lo largo de las líneas horizontales y verticales, sea la misma.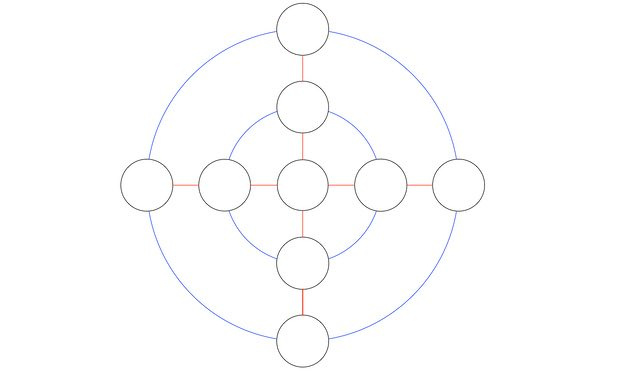



Estas son cuatro cantidades, cada una de las cuales consta de cinco términos, y todas las cantidades son iguales. Aquí hay una imagen del libro en sí, que representa una tarea similar.

Soluciones

1. En sentido horario, comenzando desde arriba: 6, 1, 8, 9

Si nombramos las posiciones para los números Norte, Este, Oeste y Sur, entonces los candidatos para el Oeste y el Sur serán 8 y 9, ya que S + 3 + 3 = 20, o S + 3 = 17. Pero sabemos que S + B + 3 = 12, o 10 + B = 9. Pero 10 no puede ser 9, porque entonces B = 0, y esto está prohibido. Por lo tanto, = = 8, 3 = 9, C = 6 y B = 1.

2. Lo que más me gustó fue la tarea enviada por un lector llamado Tom Flannery, ya que resultó ser muy simple.

Rellene los círculos con números enteros para que la suma de los sectores en cada uno de los semicírculos sea igual a la suma de los números en los círculos.

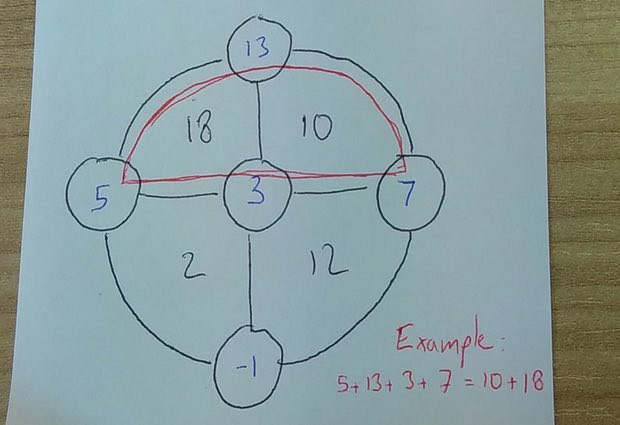
3. Y la última tarea, de la colección japonesa de acertijos de 1727.

Puede haber muchas soluciones. Aquí está mi solución:



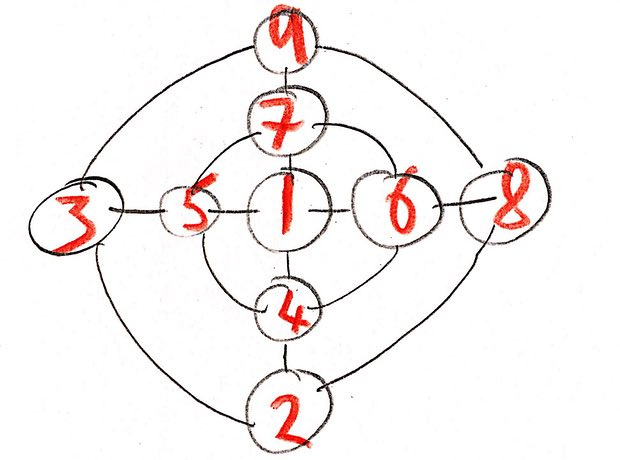
El camino hacia la solución nos ayuda a adivinar: en el centro solo puede haber un número impar. Una vez elegido ese número, debe dividir los dígitos restantes en pares que sumen el mismo número y organizarlos en círculos opuestos. Elegí 1 para el centro, respectivamente, hay pares 2 y 9, 3 y 8, 4 y 7, 5 y 6, todos dan un total de 11.