Las matemáticas nos dan una imagen precisa de respuestas casi exactas.

Usando papel grueso y cinta transparente, Craig Kaplan recoge un hermoso objeto redondeado que se asemeja a la creación de
Buckminster Fuller o un nuevo y moderno tipo de balón de fútbol. Consiste en cuatro dodecagones regulares (12 gones con los mismos ángulos y lados) y 12 decágonos (poliedros de 10 lados) con 28 pequeñas aberturas en forma de triángulos equiláteros. Solo hay un problema: esta cifra no puede existir. Tal conjunto de polígonos no coincide con los vértices, y la figura no se cierra.
El modelo Kaplan solo funciona porque cuando lo ensamblas en papel, tienes poca libertad de maniobra. Los lados pueden doblarse casi imperceptiblemente. "El margen de error derivado de trabajar en el mundo real con papel significa que las cosas que no deberían ser posibles se obtienen realmente", dice Kaplan, un científico informático de la Universidad de Waterloo en Canadá.

Este es un nuevo ejemplo de una clase de objetos matemáticos inesperados con los que el matemático estadounidense Norman Johnson se topó en la década de 1960. Johnson trabajó en la finalización de un proyecto iniciado hace más de 2000 años por Platón: creó un catálogo de formas geométricas ideales. De la infinita variedad de figuras tridimensionales, solo se pueden crear
cinco a partir de los mismos polígonos regulares: tetraedro, octaedro, hexaedro, icosaedro, dodecaedro. Si mezcla diferentes polígonos regulares, puede componer 13 formas más en las que todos los polígonos se encuentran con vértices,
cuerpos de Arquímedes , así como prismas (dos polígonos idénticos conectados por cuadrados) y "antiprismas" (dos polígonos idénticos conectados por triángulos equiláteros).
En 1966, Johnson, mientras trabajaba en la Universidad de Michigan, descubrió 92 cuerpos más que constaban solo de polígonos regulares, que ahora [en los Estados Unidos] se llaman
cuerpos de Johnson . Y esto agotó todas las posibilidades, lo que fue demostrado varios años después por el matemático ruso
Viktor Abramovich Zalgaller , quien luego trabajó en la Universidad Estatal de Leningrado. Es imposible hacer cualquier otra forma cerrada a partir de polígonos regulares.
Pero durante un inventario de los poliedros, Johnson notó algo extraño. Encontró sus formas, componiendo sus modelos de cartón y gomas elásticas. Como hay muy pocos poliedros posibles, esperaba que aparecieran nuevas formas bastante rápido. Si comienzas a hacer caras juntas, entonces la figura necesariamente debe coincidir. Pero esto no sucedió. "Al armar una pila de polígonos, no siempre era obvio si había ensamblado una forma válida", recuerda Johnson.
Puede parecer que el modelo se ha ensamblado, pero "si realiza los cálculos, resulta que esto no es del todo cierto", dice. Tras un examen cuidadoso, resultó que lo que parecía ser un cuadrado no era exactamente un cuadrado, o los lados no eran del todo planos. Sería posible recortar ligeramente las caras y encajarían perfectamente, pero ya no serían polígonos regulares.
Con la intención de calcular todas las cifras ideales, Johnson no le dio importancia a tales "golpes cercanos". "Los puse a un lado y me concentré en lo aceptable", dice. Pero estas figuras casi ideales no solo atrajeron la atención de Kaplan y otros amantes de las matemáticas, sino que se convirtieron en parte de una sección más grande de matemáticas casi ideales.
No existe una definición exacta de un golpe "casi exacto". Las reglas estrictas no funcionan en un mundo tolerante. Ahora Kaplan se guía por un método aproximado en la búsqueda de figuras casi correctas: "un error matemático real inherente a una figura es comparable a un error práctico derivado del trabajo con materiales del mundo real y manos imperfectas". En otras palabras, si lograste ensamblar un poliedro imposible, si está tan cerca de lo posible que puedes pasarlo como uno real, entonces esta será una cifra casi exacta. En otras ramas de las matemáticas, los resultados casi exactos son tan reales que pueden engañarte o sorprenderte, una especie de broma matemática.
Algunas de estas rarezas matemáticas no pueden llamarse nada más que simple diversión, mientras que otras pueden tener profundos significados en matemáticas y física.
Los antiguos problemas de
cuadrar un círculo y
doblar un cubo caen en la categoría de soluciones casi correctas. Parecen tentadores a encontrar la solución correcta, pero al final resultan imposibles, como una figura geométrica que parece cerrada pero no lo es. Algunos diseños dibujados por Leonardo da Vinci y Albrecht Durer doblaron ligeramente las esquinas, dando pentágonos casi regulares como reales.
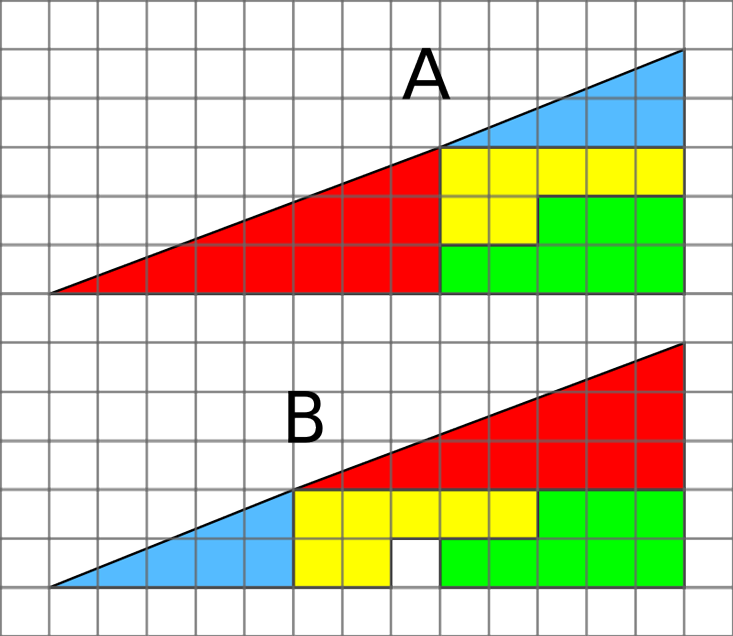
Y hay un acertijo con un cuadrado perdido. En la figura, un triángulo rectángulo se corta en cuatro partes. Si los reorganiza, aparece un espacio en él. ¿De donde vino? Esta también es casi la decisión correcta. Ninguno de los triángulos es en realidad un triángulo. Sus hipotenusas están retorcidas, y es casi imposible de notar, por eso la ilusión es tan convincente.
El emparejamiento digital es una de las decisiones más cercanas a la derecha más útiles en la vida cotidiana. 2
7/12 es casi igual a 3/2. Por una razón similar, el piano tiene 12 teclas en una octava y en el corazón del
sistema uniformemente templado de la música occidental. Este es un compromiso entre los dos intervalos musicales más importantes: una octava (frecuencia 2: 1) y una quinta (frecuencia 3: 2). Numéricamente, no es posible dividir una octava para que todos los quintos sean perfectos. Pero puede acercarse lo suficiente a esto dividiendo la octava en 12 semitonos, siete de los cuales le darán una frecuencia de 1.498. Para la mayoría de las personas, esto es suficiente.
A veces, los resultados casi exactos ocurren en las matemáticas como si se estuvieran engañando a sí mismos. En el episodio de los Simpson "Treehouse of Horror VI", el público interesado en las matemáticas notó algo inusual: la ecuación 1782
12 + 1841
12 = 1922
12 . A primera vista, puede parecer que los escritores refutaron el Gran Teorema de Fermat, postulando que la ecuación x
n + y
n = z
n no tiene soluciones enteras para n> 2. Si ingresa estos números en una calculadora de bolsillo, el resultado parecerá correcto. Pero si realiza cálculos con una precisión que no está disponible para la mayoría de las calculadoras de bolsillo, resulta que la raíz del grado 12 desde el lado izquierdo de la ecuación es 1921,999999955867 y no 1922, y Fermat puede estar tranquilo. Sorprendentemente pequeño deslizamiento: menos de 10 millones de piezas.
Pero esos golpes casi exactos no son solo bromas. "Los que me intrigan más que otros son casos que insinúan la presencia de algo más significativo", dice John Báez, matemático de la Universidad de California en Riverside. Este es el caso de una cantidad que a veces se llama la constante de
Ramanujan . Este número e
π √163 , igual a aproximadamente 262 537 412 640 768 743.9999999999999925, es sorprendentemente cercano al conjunto. No podemos esperar que estos tres números irracionales, e, π y √163, de alguna manera se combinen y nos den un número racional, sin mencionar el todo. Pero hay una razón por la que coinciden tan bien. "No es solo una coincidencia de la que no tenemos idea", dice Báez. "Esta es la clave de las profundidades de las matemáticas". La explicación exacta es bastante complicada, pero se basa en el hecho de que 163 es el mayor de los
números de Hegner . Los expositores asociados con estos números están muy cerca de los enteros.
O tome una conexión matemática conocida como la "Hipótesis monstruosa de la luz de la luna" (monstruosa luz de la luna). La historia es esta: en 1978, el matemático John Mackay hizo cuán trivial, igual de interesante, observación: 196 884 = 196 883 + 1. El primer número era un coeficiente de un polinomio importante,
invariante j , y el segundo surgió en conexión con un gran objeto matemático de la teoría de grupos. llamado "
monstruo ". Muchas personas se encogerían de hombros e irían más lejos, pero esta observación interesó a muchos matemáticos que decidieron estudiarlo más de cerca. Encontraron una conexión entre dos temas aparentemente no relacionados: la teoría de números y la simetría de los grupos Monster. Esta conexión puede tener consecuencias aún más amplias, aún no abiertas, para otros temas. El físico Edward Whitten cree que el grupo Monstruo puede asociarse con la gravedad cuántica y la estructura espacio-temporal.
Los resultados matemáticos casi correctos muestran tanto la diversión como el poder del enfoque humano de las matemáticas. Johnson, Kaplan y otros hicieron descubrimientos a través de la prueba y el error, estudiando el campo como biólogo caminando por la jungla en busca de nuevas especies. Pero en matemáticas, es más fácil realizar una búsqueda sistemática. Por ejemplo, Jim McNeill, que está interesado en las matemáticas como un pasatiempo y recopila una colección de éxitos casi correctos en su sitio, y Robert Webb, un programador, creó un software para crear y estudiar poliedros.
Los éxitos casi precisos viven en la línea borrosa entre las matemáticas ideales y duras y nuestros sentimientos condescendientes y prácticos. Vuelven de adentro hacia afuera la lógica de la aproximación. Por lo general, el mundo real se considera una sombra imperfecta del mundo de Platón. La perfección de las matemáticas subyacentes se pierde en su implementación. Pero en el caso de golpes casi precisos, el mundo real es la sombra perfecta del mundo imperfecto. La aproximación es "la aproximación incorrecta de la respuesta correcta", dice Kaplan, y "un golpe casi exacto es una representación precisa de una respuesta casi exacta".
De esta manera, las respuestas casi precisas cambian la conexión entre matemáticos y físicos matemáticos con la naturaleza. "Estoy agradecido por las imperfecciones del mundo real, porque me permiten lograr un cuasi ideal trabajando con objetos que son esencialmente imperfectos", dice Kaplan. "Me permiten superar las limitaciones de las matemáticas gracias a la belleza de una realidad rota".