Entendemos la física de partículas: 1) una bola en un resorte, la versión newtoniana

1. Bola sobre un resorte, versión newtoniana
2. Una bola cuántica en un resorte.
3. Olas, aspecto clásico
4. Ondas, la ecuación clásica del movimiento.
5. Ondas cuánticas
6. Campos
7. Las partículas son quanta
8. Cómo interactúan las partículas con los campos.

Comprender en términos generales los conceptos básicos de la física de partículas, y esta es nuestra comprensión actual de la mayoría de los fenómenos elementales del Universo, no es tan difícil. Será más fácil para usted si asistió a una escuela de física y matemática o completó el primer año de la universidad. Pero si trata con álgebra, trigonometría y (posiblemente, pero no necesariamente) los conceptos básicos de diferenciación e integración, entonces puede comprender cómo funcionan los campos y cómo aparecen las partículas. Solo necesita tomar mi palabra una vez, con respecto a un aspecto de la mecánica cuántica. En ese caso, no daré fórmulas matemáticas, sino que simplemente le mostraré las respuestas preparadas. Pero después de aceptar este aspecto, todo lo demás quedará claro.


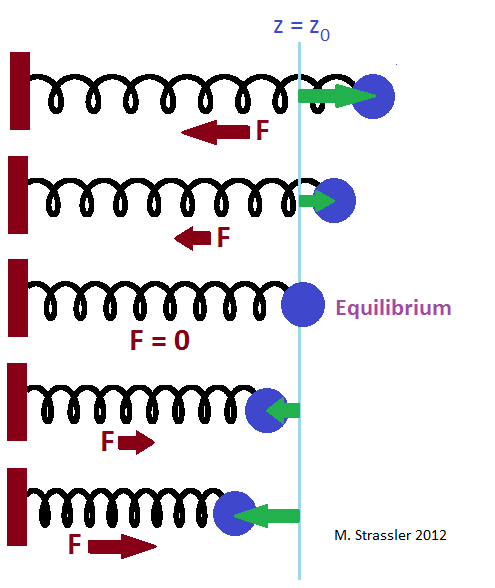Fig. 1

Para comprender la física de partículas, desde la física escolar debe recordar una sola cosa: cómo funciona un resorte. De hecho, todo lo que rebota, vibra, suena, suena, se balancea de un lado a otro, es un ejemplo de un resorte.

Imagina que colocamos una pelota al final de un resorte. Los movimientos del resorte y las ecuaciones que lo describen son simples. Para empezar, recordamos los conceptos básicos del comportamiento de la primavera, luego estudiamos el comportamiento de la pelota: la oscilación. Y finalmente, para las mentes más curiosas, consideraremos las ecuaciones que conducen a este tipo de movimiento.

Oscilador armónico (también conocido como una bola en un resorte)

La pelota en la primavera tiene una posición de equilibrio; Si coloca la pelota allí y la suelta, el resorte no la empujará en ninguna dirección y la pelota permanecerá inmóvil. Esta es la línea azul en la fig. 1. Si aleja la pelota de la posición de equilibrio (flechas verdes), el resorte tirará de la pelota hacia atrás con la fuerza F (flechas rojas). Cuanto más tire de la pelota, más fuerte la empujará el resorte (al menos hasta que rompa el resorte o lo rompa con presión).

Movimiento oscilante (salto)

Llamamos a la dirección de movimiento de la pelota "dirección z", y definimos el eje z de modo que z = z ₀ corresponda a la posición de equilibrio de la pelota en el resorte. Supongamos que tiramos la pelota desde esta posición, la sostenemos para que no se mueva, a la posición z = z ₀ + A; entonces, en cierto punto en el tiempo t = 0, lo liberamos. La pelota comenzará a saltar aquí y allá, ver fig. 2. La magnitud de los saltos (la amplitud de las oscilaciones) es igual a A. Puede ser arbitrariamente grande o pequeña; solo tú eliges cuánto tirar de la pelota desde la posición de equilibrio. Pero usted no controla con qué frecuencia se producen saltos de aquí para allá, la frecuencia de las oscilaciones ν. Resulta ser el mismo, independientemente del valor de A. Está determinado solo por las propiedades de la bola y el resorte, y no por lo que haces.

Para fines científicos, es extremadamente importante describir las observaciones a través de una fórmula matemática. La posición de la bola z es una función del tiempo t, escrita por nosotros como z (t), toma la forma:

$$

$$z (t) = z_0 + A cos [2 \ pi \ nu t]$$

Donde, como de costumbre, cos es el coseno, π es el número pi de la geometría del círculo, z ₀ es la posición de equilibrio de la bola, y A y ν (nu) son la amplitud y la frecuencia de las oscilaciones. La función coseno es oscilatoria, por lo tanto, esta fórmula describe movimientos oscilatorios con amplitud A y frecuencia ν. En la Fig. 2 se muestran ejemplos de movimiento oscilatorio de una bola sobre un resorte con diferentes valores de la desviación inicial y la amplitud total A 2, que también muestra que para una bola dada en un resorte, la frecuencia ν no depende de la amplitud A.

Letra pequeña: la amplitud y la frecuencia son mayores que cero. Si A es negativo, entonces la amplitud será –A. De hecho, la amplitud es en realidad | A |, es decir, el módulo de magnitud.


Fig. 2

Lo que es muy importante recordar acerca de la amplitud y frecuencia de la bola y el resorte (en la física clásica pre-cuántica):
• la amplitud A se puede seleccionar cualquiera;
• la frecuencia ν está determinada por la bola y el resorte, y para elegir una frecuencia diferente, debe reemplazar el resorte o la bola.

El período de cada oscilación (cuánto tiempo necesita la pelota avanzar y retroceder exactamente una vez) llamaremos a T, y este período es simplemente el recíproco de la frecuencia: T = 1 / ν. Si el período es de 5 segundos, entonces la frecuencia es una vez cada cinco segundos, o 1/5 de segundo (que a menudo se llama 1/5 Hertz o Hz).

Otra letra pequeña: en cualquier sistema real de resorte y bola que encontrará en la vida cotidiana, la fricción conducirá al hecho de que A disminuirá gradualmente y eventualmente llegará a cero cuando el movimiento se detenga. Las fórmulas que tienen en cuenta la fricción durante el movimiento no son mucho más complicadas, pero no las necesitaremos. Por lo tanto, siempre asumo que la fricción es pequeña, A disminuye muy lentamente y simplemente podemos usar fórmulas simplificadas que ignoran la fricción. Pero es importante saber: la fricción reduce A, pero, a menos que sea extremadamente fuerte, ¡no afecta a ν y T! La frecuencia de oscilación permanece igual incluso con una disminución en la amplitud. Por lo tanto, la nota que produce la cuerda de la guitarra después de tirar no cambia, incluso cuando el sonido resultante se desvanece gradualmente.

Una cosa más: hay una hermosa fórmula para la energía almacenada en un resorte oscilante. Es proporcional al cuadrado de la amplitud y al cuadrado de la frecuencia:

$$

$$E = 2 \ pi ^ 2 \ nu ^ 2 A ^ 2 M$$

En parte, esta es la energía de movimiento de la pelota (cinética), y en parte, la energía de interacción (potencial) almacenada en la primavera, y cuando la pelota se balancea hacia adelante y hacia atrás, las fracciones de estas energías en la energía total cambian constantemente. Pero la energía total E permanece constante.

Letra pequeña: todavía queda la energía de la masa de la pelota, Mc ² , pero no la rastreamos, porque siempre está ahí, el resorte se mueve con ella o no.

La misma fórmula de oscilación se aplica a casi todo lo que tiembla o salta solo si estos saltos no son demasiado grandes. Una pelota rodando por el fondo del tazón; un auto saltando sobre amortiguadores malos; cuerda vibrante de un violín o guitarra; barra de xilófono después de golpearla; etc.

La ecuación del movimiento vibratorio (saltos matemáticos)

Ahora recordemos las fórmulas básicas que nos explican por qué oscila la bola en el resorte.

Como mencionamos al principio (Fig. 1), la bola en el resorte tiene una posición de equilibrio, que llamamos z = z ₀ . Supongamos que en algún momento (o tiramos la pelota o dudó), está en una posición diferente, z. Si z> z ₀ , es decir, si el desplazamiento desde la posición de equilibrio z - z _{0 es} mayor que cero, entonces el resorte creará una fuerza dirigida en la dirección negativa z para tirar de la bola hacia el punto de equilibrio. Por el contrario, si z <z ₀ , es decir, el desplazamiento desde el equilibrio z - z _{0 es} negativo, entonces el resorte creará una fuerza dirigida en la dirección positiva z, nuevamente para tirar de la bola hacia el punto de equilibrio. Y cuanto más se aleje la pelota de la posición de equilibrio, más fuerte se moverá el resorte. La fuerza F creada por el resorte está relacionada con el desplazamiento de la bola desde el equilibrio por la ecuación

$$

$$F = - K (z - z_0)$$

Donde K es un valor positivo, dependiendo de un resorte específico, llamado la constante del resorte.

Tenga en cuenta por qué esta fórmula es verdadera:

• Si la pelota está en la posición de equilibrio, F = 0. El resorte no crea fuerza, y si la pelota no se movió en la posición de equilibrio, permanecerá allí.
• Si la desviación es mayor que cero, la fuerza es negativa.
• Si la desviación es negativa, la fuerza es positiva.
• Cuanto mayor es la desviación, mayor es la fuerza.

Luego pasamos a la segunda ley de movimiento de Newton, que establece que bajo la influencia de la fuerza F, una bola de masa M se moverá con la aceleración a, donde F = M a. Sustituya esto en la fórmula y obtenga

$$

$$M a = - K (z - z_0)$$

o

$$

$$a = - K / M (z - z_0)$$

Esta es una ecuación casi necesaria para nosotros, de la cual podemos derivar la ecuación de las oscilaciones. Solo necesitamos recordar la relación entre a y z. Para esto, es importante recordar la relación entre ay velocidad v, y entre v y z. Esta relación es uno de dos cambios a lo largo del tiempo:
• La velocidad es un cambio de posición en el tiempo, v = dz / dt
• La aceleración es un cambio en la velocidad con el tiempo, a = dv / dt

Agregar y obtener

$$

$$a = d (dz / dt) / dt = d ^ 2z / dt ^ 2$$

La aceleración es el cambio en el tiempo de un cambio de posición con el tiempo.

Podemos reescribir nuestra ecuación de ecuación de movimiento

$$

$$d ^ 2z / dt ^ 2 = - K / M (z - z_0) \ quad (*)$$

Donde z es una notación corta para z (t). Y ahora podemos verificar que el movimiento vibratorio z (t) = z ₀ + A cos [2 π ν t] será una solución para esta ecuación de movimiento. Primero tenemos que calcular la velocidad de una partícula como un cambio en su posición en el tiempo:

$$

$$d / dt (z_0 + A cos [2 \ pi \ nu t]) = - (2 \ pi \ nu) A sin [2 \ pi \ nu t]$$

(dz ₀ / dt = 0, ya que la posición de equilibrio z ₀ no cambia con el tiempo, y d / dt (cos wt) = -w sin wt); y luego calculamos la aceleración de la partícula como un cambio en su velocidad a lo largo del tiempo:

$$

$$d / dt [- (2 \ pi \ nu t)] = - (2 \ pi \ nu) ^ 2 A cos [2 \ pi \ nu t]$$

(desde d / dt (sin wt) = w cos wt). Como resultado

$$

$$d ^ 2z / dt ^ 2 = - (2 \ pi \ nu) ^ 2 A cos [2 \ pi \ nu t] = - (2 \ pi \ nu) ^ 2 (z - z_0)$$

Donde en el último paso utilicé la fórmula z (t) = z ₀ + A cos [2 π ν t] para el movimiento oscilatorio. La ecuación final es la misma que nuestra ecuación de movimiento [ $$$d ^ 2z / dt ^ 2 = - K / M (z - z_0)$], dado que (2 π ν) ² = K / M, si la frecuencia de oscilación es

$$

$$ν = \ frac {\ sqrt {K / M}} {2 \ pi}$$

Y, de hecho, descubrimos que nuestra ecuación de movimiento implica que el resorte oscilará con la frecuencia indicada, que esta frecuencia no depende de A - depende solo de las propiedades del resorte (K) y la bola (M) - y eso independientemente de cantidad A para la ecuación hay una solución. Por lo tanto, podemos elegir cualquier A, dependiendo de qué tan lejos tiremos la pelota de la posición de equilibrio antes de soltarla.

Resonancia

La resonancia es uno de los fenómenos naturales más importantes, tanto en la vida cotidiana, donde desempeña un papel en muchos aspectos de la tecnología y en la música, como en los procesos básicos del mundo físico, especialmente en la física de partículas.

Primero, recuerda cómo funciona el columpio. Un swing, como una bola en un resorte, o cualquier péndulo, es un oscilador: se balancea hacia adelante y hacia atrás con una cierta frecuencia, que no depende de la amplitud del swing. En el caso de un swing, esta afirmación sigue siendo cierta hasta que la amplitud sea muy grande. Probablemente sepa por experiencia que para balancear a un niño más alto, necesita empujar el columpio hacia adelante una vez por ciclo para que la amplitud del columpio aumente constantemente. Si empuja el swing hacia adelante varias veces por ciclo, o una vez cada dos ciclos y medio, a veces aumentará la amplitud del swing y, a veces, lo reducirá. Obviamente, hay algo especial en alinear la frecuencia con la que empuja el swing con la frecuencia natural del swing.

De manera similar, si el niño mismo sabe cómo balancear el columpio, sabe que necesita balancear las piernas al mismo tiempo que la frecuencia natural del columpio para aumentar la amplitud del columpio. Balancee de una manera diferente, y la amplitud no crecerá.



Puedes rastrear cómo sucede esto con la pelota en la primavera. Mira la foto. A la izquierda hay una bola que oscila de aquí para allá en una posición de equilibrio. Duda a sí mismo, sin choques externos. Oscila con la frecuencia natural del resorte ν. La frecuencia es √ K / M, donde K es la fuerza del resorte, M es la masa de la pelota.

A la derecha en la fig. puede ver qué le sucede a otra bola negra, la masa igual a la primera, en el mismo resorte, que se empuja con la fuerza F (su flecha roja muestra su magnitud y dirección), que oscila con una frecuencia ν _F diferente de ν. Una bola negra se comporta como un swing que empuja muy raramente; se moverán en un patrón complejo y no subirán alto. En la fig. Se puede ver que la bola no oscila muy suavemente, y la amplitud de las oscilaciones es pequeña. Puede ver cómo "trata" de oscilar con una frecuencia natural, aunque su movimiento general se repite con una frecuencia ν _F.

Luego, la figura muestra el caso en que la fuerza oscila con una frecuencia ν _F , que es mucho más alta que la frecuencia ν. Nuevamente, puede ver cómo "trata" de oscilar con una frecuencia natural, pero no logra hacerlo con una gran amplitud, ya que una fuerza que oscila rápidamente puede empujarlo hacia adentro o contra el movimiento, aumentando o disminuyendo la amplitud .

Y al final, el caso se muestra cuando la fuerza oscila con la frecuencia natural del resorte, ν _F = ν. La bola reacciona de manera muy diferente: la amplitud de las oscilaciones crece constantemente, y la bola negra oscila tan fácil y suavemente como la bola blanca de la izquierda, pero con un aumento de amplitud. Esto es una resonancia.

Como resultado: si ν _F difiere de ν - si la fuerza no permite que la pelota entre en la resonancia - se moverá, pero de mala gana, y su movimiento será muy diferente al natural, de una simple oscilación con frecuencia ν. Por el contrario, si la frecuencia de la fuerza corresponde a la natural, si la fuerza introduce la bola en resonancia, entonces la fuerza empuja la bola mucho más eficientemente, y el movimiento resultante es más impresionante. Lo sabemos intuitivamente; Al empujar el columpio con una frecuencia natural, el niño (o el padre) balancea el columpio cada vez más alto.

Entre los aspectos importantes de la resonancia en la física de partículas se encuentra el hecho de que, en ciertas circunstancias, las partículas pueden generarse debido a un mecanismo muy similar: después de una colisión de dos partículas, se obtiene una fuerza con exactamente la misma frecuencia que se requiere para crear una tercera.

La próxima vez: bola cuántica en un resorte

Este es el comportamiento de una pelota en un resorte en física clásica, pre-cuántica. La mecánica cuántica cambia muchos conceptos , pero lo más importante es esto: todavía podemos elegir A, pero A no puede ser de ningún tamaño. Solo puede tomar ciertos valores proporcionales a la raíz cuadrada de los enteros.