Entendemos la física de partículas: 3) ondas, forma clásica

1. Bola sobre un resorte, versión newtoniana
2. Una bola cuántica en un resorte.
3. Olas, aspecto clásico
4. Ondas, la ecuación clásica del movimiento.
5. Ondas cuánticas
6. Campos
7. Las partículas son quanta
8. Cómo interactúan las partículas con los campos.

Después de haber tratado las ecuaciones para las oscilaciones , que describen casi todo lo que salta, vibra, rueda de un lado a otro, como una pelota en un resorte, podemos pasar al fenómeno natural igualmente común, las ondas. Las olas están en todas partes: sonido y luz, terremotos, ondas en la superficie del estanque, etc.


Fig. 1

Pero antes de eso, te advierto que el término "onda" puede ser engañoso, ya que en física no significa lo mismo que en inglés. En física, no significa lo que normalmente llamaríamos una ola en el borde del océano: una cresta y otra hueca. En física, las ondas son una secuencia de ondas, varias crestas y canales que se mueven juntos en la misma dirección. En una ola de la forma más simple, todas las crestas son de la misma altura y están espaciadas una distancia entre sí. Consideraremos tal caso.

Las olas son un fenómeno excepcional, si lo piensas. Imagine que usted y su amigo tomaron una cuerda larga y la apretaron en la habitación (Fig. 2). Luego imagine que su amigo conversó varias veces con un extremo de la cuerda (verde). Aparecerá una ola en su extremo de la cuerda y atravesará la habitación hasta el final de la cuerda (rojo).


Fig. 2

Esto es asombroso. Quiero decir, es realmente sorprendente, fuerte y crítico para todo en nuestro universo, incluido usted personalmente. Mira lo que paso. Ninguno de los objetos físicos se movió de izquierda a derecha: antes de que su amigo comenzara a mover el extremo de la cuerda, se estiraba a través de la habitación, y al final, después de que su extremo de la cuerda deja de vibrar y la ola desaparece, la cuerda permanecerá estirada por todo el conjunto habitación, como era. Y aun así! La energía y la información se movieron por la habitación. La ola en el camino transfiere la energía gastada por su amigo en las vibraciones de la cuerda, y lleva en su forma información sobre cuántas veces y qué tan rápido la tiró, a usted, donde hace temblar su mano. Y en este caso, ella incluso te dará la mano tantas veces y en esa secuencia. Wow! Ni un solo objeto físico se movió por la habitación, y la energía y la información se movieron.

O espera ¿Pero no deberíamos considerar la ola como un objeto físico? ¿Tan físico como la cuerda misma?

Recordando esta pregunta más profunda, pasemos a una pequeña cantidad de fórmulas matemáticas necesarias para describir la apariencia y el comportamiento de una onda, y luego usemos un poco más de matemáticas para escribir ecuaciones cuyas soluciones son ondas. Esto es similar a lo que hicimos para una clásica pelota de primavera.

Fórmula para una ola infinita en un momento determinado

Esta serie de artículos inmediatamente después de que la pelota en el resorte vaya a las olas porque la onda es una especie de doble oscilador. Fluctúa tanto en el tiempo como en el espacio. Designaremos tiempo con la letra "t" y espacio con "x".

Presta atención a la fig. 3. Representa una onda que se extiende en ambas direcciones a lo largo de una gran distancia, en la que caben muchas crestas y depresiones. Esto es diferente de la ola en la fig. 2, que tiene solo algunas crestas y depresiones. Pero esta diferencia es irrelevante: en la Fig. 2 Necesitaba ilustrar para qué no importaba la forma de onda exacta; Ahora nos concentraremos en la fórmula matemática para las ondas, y es mucho más fácil hacerlo si la onda tiene una gran cantidad de crestas y depresiones del mismo tamaño. Además, este caso será muy útil para comprender cómo la mecánica cuántica afecta el comportamiento de las ondas.



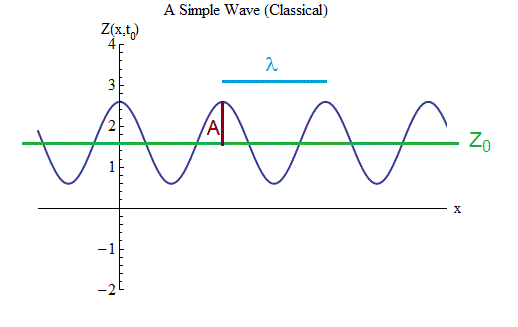
Fig. 3

Primero, necesitamos determinar la notación y escribir una fórmula que describa el movimiento y la forma de onda en la Fig. 3, como hicimos con la pelota en la primavera.

El gráfico muestra la magnitud de la onda Z en función del espacio en un cierto período de tiempo t = t ₀ : registramos esto como Z (x, t ₀ ). Al rastrear la onda en el espacio, vemos que oscila hacia adelante y hacia atrás, y Z aumenta y disminuye periódicamente. En cualquier momento, la onda oscila en el espacio.

Tenga en cuenta que Z no tiene que estar relacionado con la distancia física. Puede ser la altura de la cuerda, como en la fig. 2, o puede ser algo completamente diferente, por ejemplo, la temperatura del aire en un determinado punto en el espacio y el tiempo o la orientación de un átomo magnético en un determinado lugar de un imán. Pero x todavía representa la distancia física, y t es el tiempo.

El disparo de esta onda, Z (x, t ₀ ), tiene tres propiedades interesantes, dos de las cuales también se aplican a una pelota en un resorte.

1. Hay un valor de equilibrio Z ₀ en el medio entre el valor Z más grande en la cresta y el valor Z más pequeño en la depresión. La mayoría de las veces estudiamos ondas para las cuales Z ₀ = 0, porque a menudo el valor Z ₀ no importa, pero no siempre.
2. La onda tiene una amplitud A, un valor por el cual Z cambia del valor de equilibrio a la parte superior de cada cresta o por el mismo valor al fondo de cada depresión.
3. La ola tiene una longitud: la distancia λ entre crestas adyacentes o, lo que es lo mismo, entre canales adyacentes o, que es lo mismo, el doble de la distancia entre la cresta adyacente y el canal. Describe las oscilaciones en el espacio de la misma manera que un período (igual a 1 / frecuencia) describe la oscilación en el tiempo de una bola en un resorte.


Fig. 4 4

Lo que nos recuerda la forma en la Fig. 3? Parece una gráfica de la función seno o coseno - ver fig. 4, donde cos (w) se representa en w. Cos (w) es una función oscilante, que tiene una posición de equilibrio obvia en cero, su amplitud es 1 y la longitud de onda es 2π. Cómo ir de la fig. 4 a la fórmula para la onda en la Fig. 3? Primero, multiplicamos cos (w) por A, de modo que la amplitud sea igual a A. Luego agregamos Z ₀ a toda la fórmula para cambiarla al valor de equilibrio deseado (si A = 0, entonces no hay oscilación, y todo descansa en el punto Z = Z ₀ ). Y finalmente, reemplace w con 2πx / λ, ya que cos (w) tiene crestas en w = 0 y w = 2 π, por lo tanto, en cos (2πx / λ), las crestas estarán en x = 0 yx = λ. Todos juntos nos da

$$

$$Z (x, t_0) = Z_0 + A cos (2 \ pi x / \ lambda)$$

Esta es casi la misma fórmula que describe el movimiento de una pelota en un resorte en el tiempo:

$$

$$z (t) = z_0 + A cos (2 \ pi \ nu t) = z_0 + A cos (2 \ pi t / T)$$

Donde ν es la frecuencia de oscilación, y T = 1 / ν es el período de oscilación. Vea la analogía: un período se refiere al tiempo como una longitud de onda se refiere al espacio.

Una nota más antes de continuar. También podría escribir:

$$

$$Z (x, t_0) = Z_0 + A cos (- 2 \ pi x / \ lambda)$$

Desde cos [w] = cos [-w]. El hecho de que podamos sustituir fácilmente el signo menos en la fórmula de forma de onda será importante más adelante.

Fórmula para una ola sin fin en un lugar específico

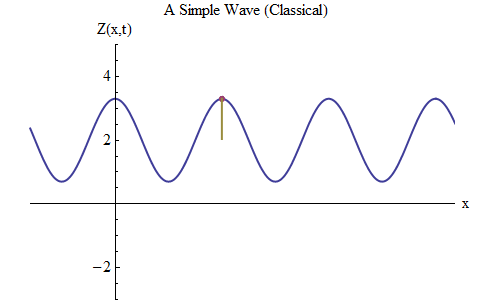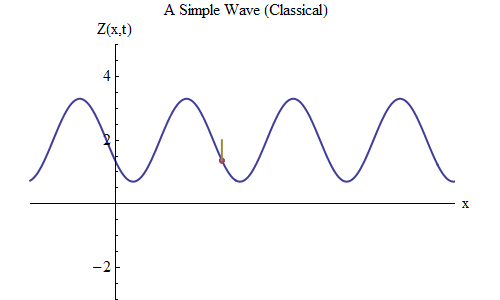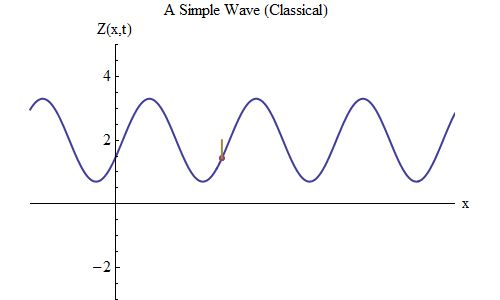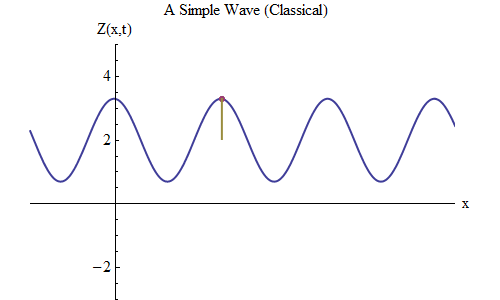Fig. 5 5

Ahora hagamos otra pregunta: veamos cómo cambia la onda en el tiempo, rastreando un cierto punto en la cuerda, y veamos cómo se comporta y se mueve. Esto se muestra en la fig. 5: allí designé un punto específico x ₀ , que en el momento t ₀ está en la cresta. La onda se mueve hacia la derecha y sigue el tamaño de la onda Z en el punto x ₀ , cambiando en el tiempo: Z (x ₀ , t). ¡Y verá de inmediato que la altura de la ola en cierto punto se comporta exactamente como una pelota en un resorte! Por lo tanto, tendrá exactamente la misma fórmula que una bola en un resorte, en función de la frecuencia ν, o período T = 1 / ν, donde T es el tiempo entre el momento en que la onda en x ₀ está en la cresta y el momento en que se acerca a la cresta la próxima vez.

$$

$$Z (x_0, t) = Z_0 + A cos (2 \ pi \ nu t) = Z_0 + A cos (2 \ pi t / T)$$

Fórmula de onda infinita completa

Ahora necesitamos una fórmula para Z (x, t) que describa la onda representada en la Fig. 3 y 5 (o uno similar) en los puntos x en cualquier momento t. La respuesta correcta es:

$$

$$Z (x, t) = Z_0 + A cos (2 \ pi [\ nu t - x / \ lambda]) = Z_0 + A cos (2 \ pi [t / T - x / \ lambda])$$

Incluye ambas fórmulas, para un punto fijo en el tiempo y para un punto fijo en el espacio.

Tenga en cuenta el signo menos delante de x. Mencioné que en la fórmula para Z (x, t ₀ ) puede sustituir un menos a voluntad. Con un signo menos delante de x y un signo más delante de t, la fórmula describe una onda que se mueve hacia la derecha, como en las animaciones. Para verificar esto, tenga en cuenta que cuando t / T - x / λ = 0, la onda será una cresta porque cos [0] = 1. Cuando t = 0, en el punto x = 0 la cresta. Pero si avanzamos t un poco hacia adelante, digamos, en T / 10, entonces la cresta estará en el punto x = λ / 10, a la derecha del lugar donde estaba en t = 0, por lo tanto, la cresta (y toda la onda) se mueve hacia la derecha.

¿Qué cambiará si coloca un más en lugar de un menos en la fórmula para Z (x, t)? Entonces la cresta estará en t / T + x / λ = 0, y en este caso, en t = T / 10, la cresta estará en x = -λ / 10, a la izquierda del lugar donde estaba en t = 0, lo que significa , ahora la ola se mueve hacia la izquierda (Fig. 6).


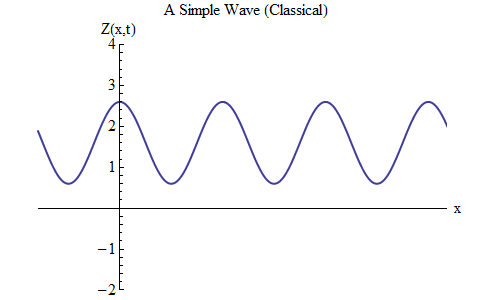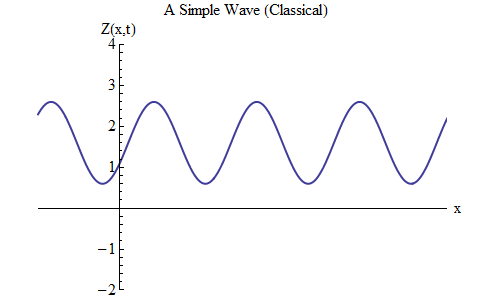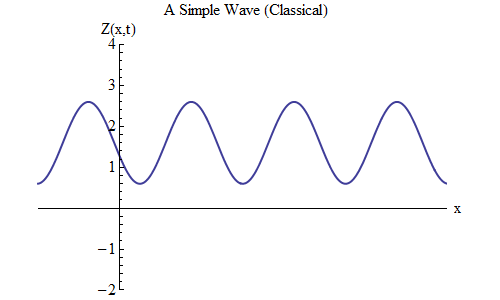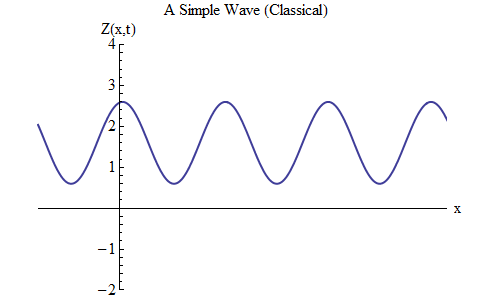Fig. 6 6

Las ondas, que son funciones de x y t, pueden moverse en cualquier dirección, por lo que solo tenemos que elegir la fórmula correcta para la onda dada. En términos generales, cuando trabajamos con ondas que pueden moverse no solo a lo largo de una dimensión espacial x, sino a lo largo de las tres coordenadas x, y y z, estas ondas pueden moverse en cualquier dirección, y tendremos que elegir la fórmula correcta en función de la dirección movimiento ondulatorio

Letra pequeña: podemos poner un signo menos delante de t, y no antes de x. Pero + t, + x es lo mismo que –t, -x, porque será equivalente a multiplicar toda la fórmula dentro del coseno por -1, y cos [w] = cos [-w]. Por lo tanto, + t, + x y -t, -x dan una onda que se mueve hacia la izquierda, y + t, -x y -t, + x dan una onda que se mueve hacia la derecha.

Ecuación de onda

Ahora, como en el caso de una pelota en un resorte, cuando encontramos por primera vez una fórmula para el movimiento oscilatorio de la pelota, y luego observamos la ecuación de movimiento, para la cual esta fórmula era una solución, haremos lo mismo aquí. Encontramos una fórmula para la forma y el movimiento de la ola. ¿Qué ecuación de movimiento entre las soluciones tiene tal fórmula? Aprendemos en el próximo artículo.