Entendemos la física de partículas: 4) ondas, la ecuación clásica del movimiento

1. Bola sobre un resorte, versión newtoniana
2. Una bola cuántica en un resorte.
3. Olas, aspecto clásico
4. Ondas, la ecuación clásica del movimiento.
5. Ondas cuánticas
6. Campos
7. Las partículas son quanta
8. Cómo interactúan las partículas con los campos.

Volvamos a la ecuación de las oscilaciones de una bola en un resorte.

En uno de los primeros artículos del ciclo, primero derivamos una fórmula para el movimiento oscilatorio de una pelota

$$

$$z (t) = z_0 + A cos [2 \ pi \ nu t]$$

Y luego encontraron la ecuación de movimiento para la cual esta fórmula era una solución

$$

$$d ^ 2z / dt ^ 2 = - K / M (z - z_0)$$

Aqui
• d ² z / dt ² denota un cambio en el tiempo sobre un cambio en el tiempo z (t).
• K es la fuerza del resorte, M es la masa de la pelota, z ₀ es la posición de equilibrio.
• ν = √ K / M / 2π

El paso clave para obtener la última ecuación de frecuencia expresada en términos de K y M fue el cálculo de d ² z / dt ² para el movimiento oscilatorio de la bola z (t) = z ₀ + A cos [2 π ν t]. Encontramos que

$$

$$d ^ 2z / dt ^ 2 = - (2 \ pi \ nu) ^ 2 (z - z_0)$$

Ecuación de onda

Ahora queremos hacer lo mismo para las olas. Encontramos una fórmula para la forma y el movimiento de una onda que oscila tanto en el espacio como en el tiempo.

$$

$$Z (x, t) = Z_0 + A cos (2 \ pi [\ nu t - x / \ lambda]) = Z_0 + A cos (2 \ pi [t / T - x / \ lambda])$$

¿Entre las soluciones de qué ecuación de movimiento está esa fórmula? Puedes imaginar la respuesta. Obviamente, incluye:

1. d ² Z / dt ² , cambio en el tiempo, cambio en el tiempo Z (x, t).
2. d ² Z / dx ² , un cambio en el espacio de un cambio en el espacio Z (x, t).

Naturalmente, podemos adivinar que la ecuación debería verse así:

$$

$$C_t d ^ 2Z / dt ^ 2 + C_x d ^ 2Z / dx ^ 2 = C_0 (Z - Z_0)$$

Donde C _t , C _x y C ₀ son constantes. Observo que si Donde C _t = 1, C _x = 0 y C ₀ = -K / M, volveremos a la ecuación de oscilación de la bola en el resorte. ¿Cuáles son estas constantes en nuestro caso?

Siempre podemos poner C _t = 1. Si quisiera, digamos, poner C _t = 5, simplemente le pediría que divida la ecuación completa por 5, lo que le daría el equivalente de la opción en la que C _t = 1, solo con otros valores de otras constantes.

Después de eso, resulta que los valores de C _x y C ₀ resultan ser diferentes en diferentes sistemas físicos. Estudiaremos dos clases diferentes de ondas con constantes diferentes.

Para ambas clases, C _x será negativo, $$$C_x = -c_w ^ 2$(aquí c _w denota la velocidad de movimiento de las ondas de alta frecuencia).

Estas clases diferirán en que la primera clase, Clase 1, C ₀ será negativa y será - (2 π μ) 2, y la segunda, Clase 0, C ₀ será cero.

Ahora estudiamos las propiedades de las ondas de estas dos clases de ecuaciones. Pero antes de eso, necesitamos realizar otro cálculo, que ya hicimos antes.

Recuento rápido

Para nuestra ola interminable

$$

$$Z (x, t) = Z_0 + A cos (2 \ pi [\ nu t - x / \ lambda]) = Z_0 + A cos (2 \ pi [t / T - x / \ lambda])$$

Necesitaremos saber d ² Z / dt ² y d ² Z / dx ² . En el artículo anterior, ya mostramos que para una bola en un resorte que se mueve de acuerdo con z (t) = z ₀ + A cos [2 π ν t], resulta que $$$d ^ 2z / dt ^ 2 = - (2 \ pi \ nu) ^ 2 (z - z_0)$. Un cambio en el tiempo nos da un factor de 2 π ν, y un cambio en el tiempo nos da un factor de dos factores. Además, hay un signo menos común. Por lo tanto, no te sorprenderá que:

• $$$d ^ 2Z / dt ^ 2 = - (2 \ pi \ nu) ^ 2 (Z - Z_0)$
• $$$d ^ 2Z / dx ^ 2 = - (2 \ pi / \ lambda) ^ 2 (Z - Z_0)$

Cada cambio en el tiempo nos da el factor ν = 1 / T (cuanto mayor es el período, más lento es el cambio en el tiempo), y cada cambio en el espacio nos da el factor 1 / λ (cuanto más larga es la onda, más lento es el cambio en el espacio).

Prueba

Para una onda infinita, tenemos la ecuación básica.

$$

$$Z (x, t) = Z_0 + A cos (2 \ pi [\ nu t - x / \ lambda]) = Z_0 + A cos (2 \ pi [t / T - x / \ lambda])$$

Y queremos mostrar que

$$

$$d ^ 2Z / dt ^ 2 = - (2 \ pi \ nu) ^ 2 (Z - Z_0)$$

$$

$$d ^ 2Z / dx ^ 2 = - (2 \ pi / \ lambda) ^ 2 (Z - Z_0)$$

Algunos hechos:

• Z - Z ₀ = A cos (2π [ν t - x / λ]) (solo en la ecuación principal movieron Z ₀ al lado izquierdo)
• Dado que Z ₀ es una constante independiente del tiempo y el espacio, dZ ₀ / dt = 0 y dZ ₀ / dx = 0.
• d (cos t) / dt = - sen t, y d (sin t) / dt = + cos t
• d (F [at + bx]) / dt = ad (F [at + bx]) / d (a t + bx), donde a y b son constantes, y F es cualquier función de (at + bx).
• d [A f (t)] / dt = A d [f (t)] / dt, donde f (t) es cualquier función de t, y A es una constante

Juntos, esto significa que:

$$

$$dZ / dt = d [A cos (2 \ pi [\ nu t - x / \ lambda])] / dt = cos (2 \ pi [\ nu t - x / \ lambda])] / dt \\ = A (2 \ pi \ nu) d [cos (2 \ pi [\ nu t - x / \ lambda])] / d (2 \ pi [\ nu t - x / \ lambda]) = - ( 2 \ pi \ nu) A sin (2 \ pi [\ nu t - x / \ lambda])$$

y

$$

$$d ^ 2Z / dt ^ 2 = d [- (2 \ pi \ nu) A sin (2 \ pi [\ nu t - x / \ lambda])] / dt = \\ - (2 \ pi \ nu) A d [sin (2 \ pi [\ nu t - x / \ lambda])] / dt = \\ - (2 \ pi \ nu) ^ 2 A cos (2 \ pi [\ nu t - x / \ lambda ]) = - (2 \ pi \ nu) ^ 2 (Z - Z_0)$$

Dado que la fórmula básica de la onda no cambia cuando (ν t) se reemplaza por (-x / λ), el cálculo de d ² Z / dx ² no difiere del cálculo de d ² Z / dt ² , solo que en lugar de d / dt da el factor (2π ν ), tendremos d / dx dando el factor (- 2π / λ). Pero, dado que hay dos factores en la respuesta, simplemente reemplazamos (2π ν) ² con (- 2π / λ) ² = (+ 2π / λ) ² ; menos no importa (la suma total menos permanece). Como necesitábamos probar

$$

$$d ^ 2Z / dt ^ 2 = - (2 \ pi / \ lambda) ^ 2 (Z - Z_0)$$

Letra pequeña: todos los derivados anteriores son, de hecho, derivados parciales.

Clase 0: ondas de cualquier frecuencia e igual velocidad

En esta clase de ondas, la ecuación de movimiento será:

$$

$$d ^ 2Z / dt ^ 2 - c_w ^ 2 d ^ 2Z / dx ^ 2 = 0$$

Después de haber conectado la fórmula Z (x, t) para una onda infinita y utilizando los cálculos que acabamos de hacer, encontramos que:

$$

$$- (2 \ pi \ nu) ^ 2 (Z - Z_0) - (-c_w ^ 2) (2 \ pi / \ lambda) ^ 2 (Z - Z_0) = 0$$

Divide la ecuación por $$$- (2 \ pi) ^ 2 (Z - Z_0)$tenemos

$$

$$\ nu ^ 2 - c_w ^ 2 / \ lambda ^ 2 = 0$$

Dado que las frecuencias, velocidades y longitudes de onda son positivas, podemos extraer la raíz y obtener

ν = c _w / λ, o, si lo desea, λ = c _w / ν = c _w T

De esta fórmula aprendemos que:

• Inicialmente, nuestra onda, tal como la registramos, podría tener cualquier frecuencia y cualquier longitud de onda. Pero la ecuación de movimiento los hace depender unos de otros. Para las ondas de clase 0, puede elegir cualquier frecuencia, pero después de eso la longitud de onda se determina a través de λ = c _w / ν.
• Todas las ondas de la clase 0, independientemente de la frecuencia, viajan con velocidad c _w . Esto se deduce de la fórmula λ = c _w T y la Fig. 3 del artículo anterior . Observe cómo la onda atraviesa un ciclo de oscilaciones durante un período de T. ¿Qué está sucediendo? La onda se ve exactamente igual después de T, pero cada cresta se ha desplazado hacia donde estaba su vecina, a una distancia λ. Esto significa que la cresta se mueve una distancia λ en el tiempo T - una longitud de onda en un período de oscilación - y significa que las crestas se mueven a una velocidad de λ / T = c _w . ¡Esto es cierto para todas las frecuencias y sus períodos, y para todas las longitudes de onda!
• Como en el caso de una pelota en un resorte, la amplitud A de estas ondas puede ser cualquiera, arbitrariamente grande o pequeña. Y este es el caso para todas las frecuencias.

Clase 1: ondas con una frecuencia superior al mínimo, con diferentes velocidades

Para esta clase de ondas, nuestra ecuación de movimiento será:

$$

$$d ^ 2Z / dt ^ 2 - cw ^ 2 d ^ 2Z / dx ^ 2 = - (2 \ pi \ mu) ^ 2 (Z - Z_0)$$

Sustituyendo la fórmula Z (x, t) por una onda infinita y usando el cálculo rápido indicado arriba, encontramos que

$$

$$- (2 \ pi \ nu) ^ 2 (Z - Z_0) - (-cw ^ 2) (2 \ pi / \ lambda) ^ 2 (Z - Z_0) = - (2 \ pi \ mu) ^ 2 ( Z - Z_0)$$

Dividiendo la ecuación por $$$- (2 \ pi) ^ 2 (Z - Z_0)$tenemos

$$

$$\ nu ^ 2 - cw ^ 2 / \ lambda ^ 2 = \ mu ^ 2$$

Como las frecuencias, velocidades y longitudes de onda son positivas, podemos extraer la raíz cuadrada y obtener

$$

$$\ nu = [(cw / \ lambda) ^ 2 + \ mu ^ 2] ^ {1/2}$$

Permíteme recordarte que y ^1/2 es lo mismo que √y.

Esta fórmula es muy diferente de la fórmula para las ondas de clase 0, como lo son las consecuencias de su aplicación.

Primero, la ecuación de movimiento indica la presencia de la frecuencia mínima permitida. Como (cw / λ) ² siempre ^es positivo,

$$

$$\ nu = [(cw / \ lambda) ^ 2 + \ mu ^ 2] ^ {1/2} ≥ \ mu$$

Para acercarse a ν = μ, es necesario aumentar λ. Para longitudes de onda muy grandes, la frecuencia se aproxima a μ, pero no puede volverse más pequeña. Para las ondas de clase 0, esto no fue así. Tenían ν = cw / λ, así que para ellos, cuanto más hagas λ, más fuerte ν se acerca a cero. Para ondas de clase 1, cualquier valor de ν mayor que μ es posible.

En segundo lugar, encontramos evidencia de que todas las ondas de la clase 0 tienen la misma velocidad, pero no funciona para las ondas de la clase 1. La única opción en la que puede funcionar si tomamos ν es mucho más grande que μ; para esto necesitamos hacer λ muy pequeño (y, en consecuencia, 1 / λ muy grande). En este caso

$$

$$\ nu = [(cw / \ lambda) ^ 2 + \ mu ^ 2] ^ {1/2} ≈ cw / \ lambda$$

Es decir, a frecuencias muy grandes y longitudes de onda pequeñas, las ondas de clase 1 tendrán aproximadamente la misma relación entre frecuencia y longitud de onda que las ondas de clase 0, por lo tanto, por las mismas razones que las ondas de clase 0, tales ondas se moverán a una velocidad , (aproximadamente) igual a cw.

Lo que es cierto para las ondas de ambas clases es que la amplitud A puede ser cualquiera, arbitrariamente pequeña o grande, y no depende de la frecuencia.


Fig. 1. Para las ondas de clase 0 y 1, la ecuación de movimiento da una relación entre frecuencia, o período, y longitud de onda, o 1 / longitud de onda. Cada uno de los gráficos muestra la relación de estos valores dependiendo de la ecuación de movimiento. Tres gráficos muestran lo mismo, pero se basan en diferentes variables. Las líneas azules se refieren a ondas de clase 0. Las rojas indican ondas de clase 1, cuya velocidad es la misma a frecuencias muy altas y longitudes de onda cortas, cuando coinciden con las líneas azules. Pero a la frecuencia mínima μ (y con un período máximo de 1 / μ), marcado en verde, las dos curvas divergen con el aumento de las longitudes de onda.

Letra pequeña: puede que hayas notado que hice un poco de trampa. No calculé la velocidad de las olas de la clase 1. El hecho es que una captura muy difícil acechaba aquí. Para las olas de clase 0, conté su velocidad, siguiendo los movimientos de las crestas. Esto funciona porque en la clase 0, las ondas de todas las frecuencias viajan a la misma velocidad. Pero en la clase 1, o en cualquier otra, donde las ondas de diferentes frecuencias se mueven a diferentes velocidades, ¡la velocidad de una onda real no está determinada por la velocidad de movimiento de sus crestas! Resulta que las crestas se mueven más rápido que cw, pero la velocidad de la onda es menor que cw. Para comprender esto, es necesario utilizar una lógica muy poco obvia y la diferencia entre la velocidad de "grupo" y "fase". Pasaré por alto este truco; Solo quería llamar su atención sobre su existencia para que no tenga una idea equivocada.

Comentarios finales sobre olas clásicas

Puede encontrar muchos ejemplos familiares de ondas de Clase 0, incluido el sonido en el aire, el agua o el metal (donde cw es la velocidad de las ondas de sonido en un material), la luz y otras ondas electromagnéticas (donde cw = c en el vacío) y ondas en cuerdas o cuerdas, como en la fig. 2 en el artículo anterior. Por lo tanto, las ondas de clase 0 se imparten en cursos de física de primaria. No puedo dar un ejemplo de las ondas de Clase 1 en la vida cotidiana, pero pronto veremos que estas ondas también son importantes para el Universo.

Tenemos una fórmula conveniente E = 2 π ² ν ² A ² M para la energía de una bola de masa M en un resorte. Las fórmulas para otros osciladores dependen de su naturaleza, pero su forma es casi la misma. Pero en el caso de las olas, no mencionamos su energía. En particular, porque estudiamos ondas con un número infinito de crestas para simplificar las matemáticas. Intuitivamente, se debe almacenar algún tipo de energía en el movimiento y la forma de cada cresta y valle, y con un número infinito de crestas y canales, la cantidad de energía en la onda será infinita. Hay dos formas de evitar esto. Las fórmulas exactas dependen del tipo de onda, pero veamos las ondas de clase 0 en una cuerda.

• La cantidad de energía por longitud de onda (almacenada entre el punto xy el punto x + λ), por supuesto, es igual a 2 π ² ν ² A ² M _λ , donde M _λ es la masa del segmento de cuerda de longitud λ.
• En realidad, las ondas no son infinitas. Como un impulso de varias crestas y depresiones, que se muestra en la Fig. 2 en el último artículo, cualquier ola será finita, tendrá un número finito de crestas y depresiones. Si se estira a una longitud L, es decir, tendrá crestas L / λ, entonces la energía transferida será 2 π ² ν ² A ² M _L , donde M _L es la masa de un trozo de cuerda de longitud L. Esto es solo L / λ, multiplicado por energía por una longitud de onda.

Para las ondas que se propagan de las cuerdas, los detalles de las ecuaciones serán diferentes, pero la energía por longitud de onda de un sistema oscilatorio simple siempre será proporcional a ν ² A ² .

En la clase 1, hay una onda muy interesante, que no existe en la clase 0. Este es el caso cuando ν = μ, el valor mínimo y λ = infinito. En este caso, la ola toma la forma

$$

$$Z (x, t) = Z_0 + A cos (2 \ pi \ mu t)$$

Esta onda no depende de x en ningún momento, es decir, Z (x, t) será una constante en todo el espacio, y Z oscila en el tiempo como una bola en un resorte con una frecuencia μ. Tal onda estacionaria, que se muestra en la Fig. 2, será muy importante en otras consideraciones.


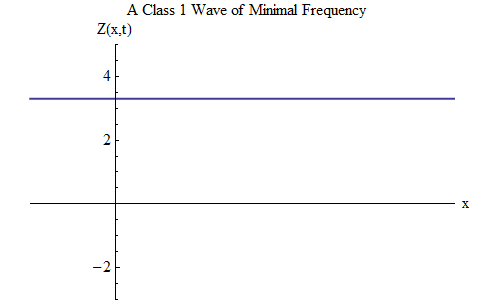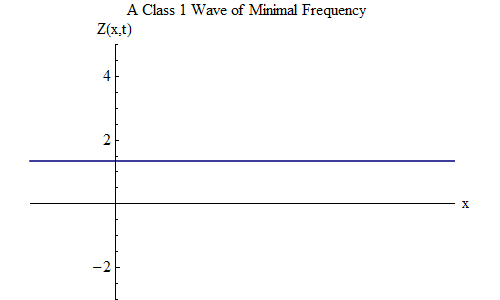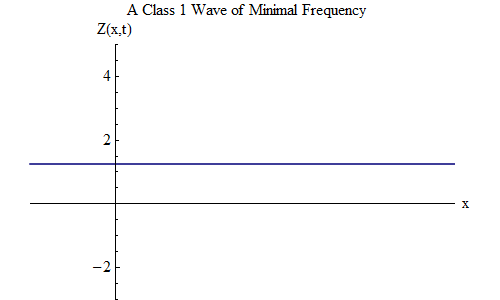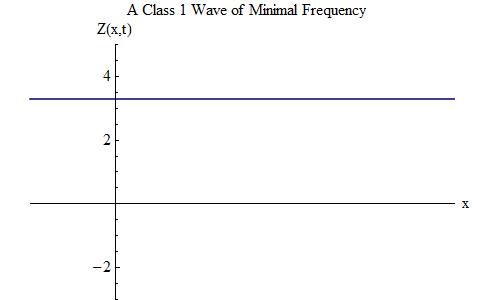Fig. 2

Ondas cuánticas

Para una pelota en un resorte, la diferencia entre los sistemas clásico y cuántico era que, en el primer caso, la amplitud podía tomar valores arbitrarios, como la energía, y en el caso cuántico, la amplitud y la energía se cuantificaban. Para cualquier sistema oscilatorio similar, esto funciona de la misma manera. Quizás podamos adivinar que esto también es cierto para las olas ...