Entendemos la física de partículas: 6) campos

1. Bola sobre un resorte, versión newtoniana
2. Una bola cuántica en un resorte.
3. Olas, aspecto clásico
4. Ondas, la ecuación clásica del movimiento.
5. Ondas cuánticas
6. Campos
7. Las partículas son quanta
8. Cómo interactúan las partículas con los campos.

De hecho, entramos en el territorio del campo hace algún tiempo, simplemente no te lo advertí, quería concentrarme en las olas que surgen en estos campos. Al describir cómo se comportan las ondas, expresamos su forma y dependencia del tiempo utilizando la función Z (x, t). Bueno, Z (x, t) es un campo. Esta es una función del espacio y el tiempo con una ecuación de movimiento que determina su comportamiento. Una función de movimiento adecuada sería tal que si Z aumenta o disminuye en un cierto punto, Z disminuirá o aumentará en los puntos vecinos un poco más tarde. Esta característica permite que las ondas estén entre las soluciones de la ecuación.

En este artículo, veremos algunos ejemplos de campos Z (x, t) cuyas ecuaciones de movimiento permiten la presencia de ondas. La interpretación física de estos campos será muy diferente. Describen las diferentes propiedades de diferentes materiales. Pero las ecuaciones que satisfacen, y las ondas que demuestran, satisfarán matemáticas muy similares y se comportarán de manera similar, a pesar de sus diferentes orígenes físicos. Este será un punto muy importante en el futuro.

Y luego hacemos algo radical: consideremos los campos en el contexto de la teoría especial de la relatividad. Como mostró Einstein, si corrige el espacio y el tiempo y los obliga a liderar no de la manera que la mayoría de la gente espera, obtendrá un nuevo tipo de campo, de modo que su interpretación física no es una propiedad de otra cosa, sino un objeto físico independiente.

Campos ordinarios que describen cosas ordinarias.

El campo Z (x, t) puede representar muchas cantidades físicas diferentes. Por ejemplo:
• La altura de la cuerda se extendía por la habitación.
• La altura del agua en el río.
• La densidad del cristal o gas.
• La posición de los átomos en un imán.
• Velocidad del viento.
• Temperatura, densidad o presión del aire.

En cualquiera de estos casos, hay un campo Z (x, t): un campo de altura, un campo de densidad, un campo de orientación, un campo de viento y un campo de temperatura. Su valor en forma de función de espacio y tiempo nos dice la altura, la densidad, la orientación, la velocidad del viento o la temperatura de un medio (una cuerda, río, cristal, gas, imán, aire) en todos los lugares en cualquier momento. Su ecuación de movimiento muestra cómo Z (x, t) puede comportarse en principio. También muestra cómo predecir el comportamiento de Z (x, t) en el futuro, si conocemos exactamente su comportamiento en el presente y el pasado.

En cada ejemplo, hay un campo y un entorno, y no debemos confundir el campo con el entorno. El campo simplemente describe y caracteriza una de las muchas propiedades del entorno correspondiente. Ambientes absolutamente diferentes pueden tener campos de comportamiento muy similares con ondas muy similares, todavía lo veremos.

Una vez más aclararé un punto que a menudo causa malentendidos. En general, un campo puede no tener nada que ver con la distancia física en el espacio. Sí, en los artículos 3 y 4, utilicé el ejemplo de un buey en una cuerda para ilustrar lo que Z (x, t) puede ser, porque es hermoso e intuitivo. También a menudo tracé gráficos Z (x, t) para las ondas. Esto puede darle la falsa impresión de que Z (x, t) siempre está asociado con ondas que hacen que un objeto físico (como una cuerda) se mueva una distancia Z en una dirección perpendicular al eje x. Pero esto no es así, como lo demostrarán tres de nuestros cuatro ejemplos.

Campo de altura de cuerda

Primero, considere nuestro ejemplo inicial de ondas, una cuerda oscilante. En este caso, el papel de Z (x, t) es el campo de altura, que llamamos H (x, t). Nos dice la altura de la cuerda en cada punto del espacio en el eje x que corre a lo largo de la cuerda en cualquier momento t. Si la cuerda está a la altura de equilibrio H ₀ , entonces H (x, t) = H ₀ . El campo de altura es una constante en el espacio y el tiempo. Si una ola simple se mueve a través de ella, entonces el campo de altura será descrito por nuestra famosa fórmula de ola de artículos anteriores.

Si conocemos H (x, t), sabemos la altura de la cuerda en todos los puntos en el espacio y el tiempo. Si sabemos lo que está haciendo la cuerda ahora y lo que ha estado haciendo recientemente, utilizando la ecuación de movimiento podemos predecir lo que hará en el futuro. Esto nos dice poco sobre la cuerda en sí. El campo de altura solo nos da lo que su nombre implica: la altura de la cuerda. Una cuerda es un medio físico cuya altura se representa como un campo H (x, t); no nos dice nada sobre el color de la cuerda, su grosor, tensión, material, etc.

En la fig. 1 Te hice una animación de una ola en un campo de altura de izquierda a derecha. Puede parecer que pinté lo mismo dos veces, primero en verde y luego en naranja. Pero esto no es lo mismo. La curva naranja es la cuerda misma, que se mueve en el espacio físico. Una curva verde es un gráfico que representa lo que está sucediendo con H (x, t), independientemente de lo que H (x, t) (es decir, la altura) signifique, o de qué tipo de entorno sea. Y solo en este caso, el gráfico verde se ve exactamente igual a lo que está sucediendo en el mundo físico. Pero en todos los demás casos esto no será así.


Fig. 1

Campo de desplazamiento de celosía

Supongamos que tenemos un medio que consiste en un cristal con átomos distribuidos uniformemente a distancias iguales entre sí. Los dibujé en la foto. 2 en una dimensión: puede imaginar situaciones similares con tres dimensiones, pero por ahora esto sería una complicación innecesaria. También marqué cada décimo átomo en rojo para que sea más fácil seguir su movimiento. Y también exageré mucho la distancia entre los átomos: imagine que entre cada dos puntos rojos hay varios millones de átomos, no 10.

Observamos el campo de desplazamiento D (x, t), que nos dice cuánto en el momento t el átomo, generalmente ubicado en el punto de equilibrio x, se ha movido desde este punto en la red. Esto significa que en el caso de un estado estático desde el que comienza la animación, el campo está en todas partes cero, D (x, t) = 0, ya que todos los átomos están en su posición habitual. Luego, en la animación, los átomos individuales comienzan a oscilar de un lado a otro, y su movimiento, en general, se propaga en forma de onda que va de izquierda a derecha. En la parte superior de la figura, la gráfica del campo de desplazamiento de la red D (x, t) muestra cómo se comporta el campo durante el paso de la onda. Tenga en cuenta que los campos en la Fig. 1 y 2 se comportan de manera similar, aunque la interpretación física de los campos es muy diferente.


Fig. 2

Campo de orientación magnética

¿Qué es un imán permanente? Consiste en un conjunto de átomos, cada uno de los cuales sirve como un pequeño imán con un pequeño campo magnético, y todos están alineados para que juntos creen un gran campo magnético. El imán se muestra en la fig. 3, y en él cada átomo se dirige hacia arriba. En este caso, el campo de orientación Θ (x, t) nos dice qué tan lejos en el tiempo t el átomo en el punto x se desvió de la vertical. Θ, en resumen, será el ángulo entre el imán de cada átomo y la vertical. La animación en la fig. 3 muestra una onda en un imán en el que las direcciones de los imanes atómicos oscilan hacia la izquierda y hacia la derecha. Se muestra un gráfico Θ (x, t) sobre el imán verde; y nuevamente se ve exactamente igual que en casos anteriores.

Campo de presión de aire

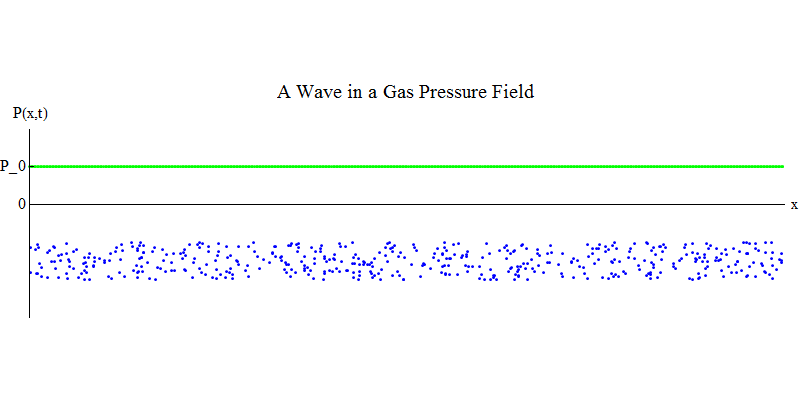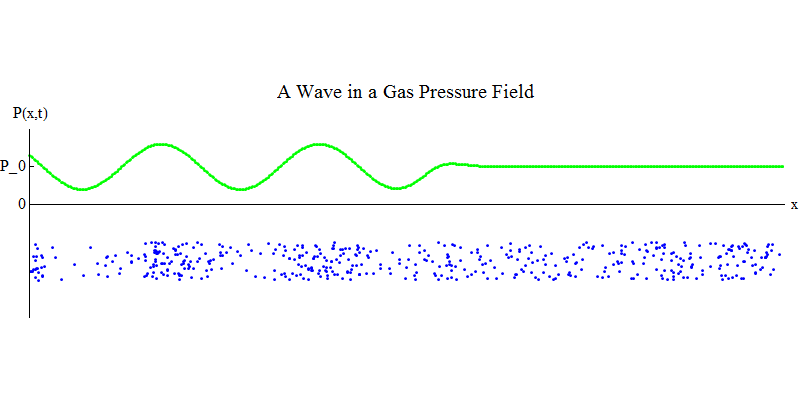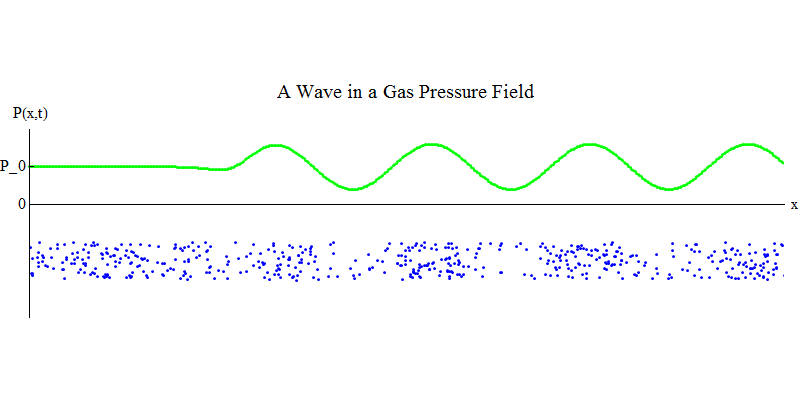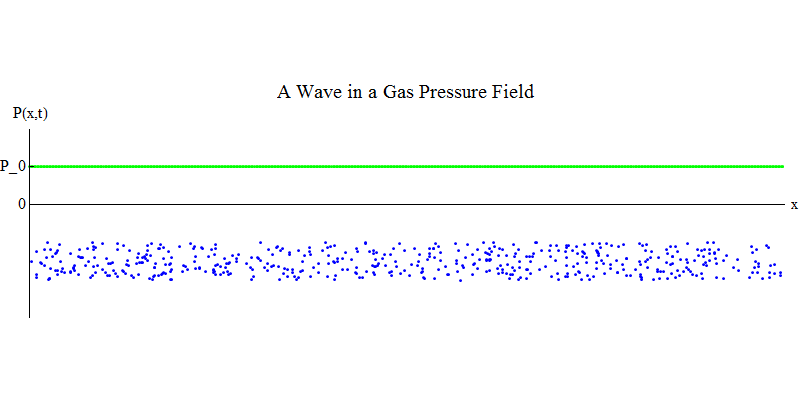
Considere un gas molecular en una tubería larga. A lo largo de la tubería estará la dimensión x. Las moléculas de gas se moverán casi al azar, chocando con las paredes de la tubería y entre sí. En equilibrio, la densidad (el número de moléculas en un cierto volumen) y la presión P (x, t) (la fuerza que actúa sobre la superficie de una pequeña bola que apareció en el punto x en el tiempo t) son constantes. Pero las ondas de sonido que pasan a través del gas harán que la presión y la densidad oscilen, como se muestra en la fig. 4. La densidad y la presión aumentan y disminuyen periódicamente. Las moléculas se mueven hacia adelante y hacia atrás, aunque en promedio no se mueven en absoluto, pero al mismo tiempo la ola y su energía se mueven de izquierda a derecha a través del gas. El gráfico P (x, t) se ve nuevamente muy similar a los anteriores.

Lecciones importantes

¿Qué podemos aprender de cuatro ejemplos que muestran ondas de clase 0? (La ecuación de movimiento tiene una cantidad, cw, y todas las ondas en el campo correspondiente se mueven con velocidad cw. Los diferentes campos de la clase 0 tendrán diferentes valores de cw). Podemos descubrir que el mismo comportamiento de campo puede surgir de campos físicamente diferentes que existen en entornos físicamente diferentes. A pesar de su origen diferente, las ondas en el campo de altura, en el campo de desplazamiento de la red, en el campo de orientación magnética y en el campo de presión de gas se ven idénticas desde el punto de vista de los campos. Satisfacen el mismo tipo de ecuación de movimiento y la misma relación numérica de frecuencia y longitud de onda.

Letra pequeña: estrictamente hablando, si crea ondas de una longitud suficientemente corta, aún puede distinguir el comportamiento de diferentes medios. Tan pronto como las longitudes de onda sean iguales a la distancia entre los átomos de la cuerda, el cristal o el imán, las ecuaciones de onda que satisfarán las ondas serán más complejas que las escritas por nosotros, y sus detalles distinguirán los medios entre sí. Pero a menudo en experimentos prácticos ni siquiera nos acercamos a observar tales efectos.

El resultado de esto es que el estudio de las ondas y sus cuantos relacionados con los campos no necesariamente le dirá qué sirve como medio, o cuál es la interpretación física del campo, cuál de las propiedades del medio es. E incluso si de alguna manera sabe que este es un campo de cierto tipo, por ejemplo, un campo de presión, por lo general aún no podrá saber por su comportamiento qué presión representa. Todo lo que puede aprender al estudiar las ondas es si el campo pertenece a la clase 0 o clase 1, y cuál es el valor de cw; o descubra que el campo pertenece a otra clase.

En algunos casos, esto es muy malo; el campo transmite solo información parcial sobre el entorno. Esto a veces es bastante conveniente; El campo es algo más abstracto y universal que el material físico que describe.

Por lo tanto, el campo no define el entorno y su comportamiento a menudo no depende de los detalles y propiedades del entorno. Por lo que surge la pregunta.

¿Podría existir un campo físico, con ondas que consisten en cuantos que se mueven en el espacio y transfieren energía, sin ningún medio que lo soporte?

Campo sin medio?

No puedes escuchar una canción sin un cantante. Pero la canción tiene algún tipo de existencia independiente; suena de manera diferente, dependiendo de quién la canta, pero al mismo tiempo hay algo inherente en la canción, algo de calidad abstracta, gracias a la cual siempre se puede reconocer. Esta entidad abstracta es la melodía de la canción. Podemos discutir, estudiar, aprender una melodía, grabarla con una grabación musical, sin siquiera escucharla interpretada por el cantante. Muchos de nosotros incluso podemos tararearlo en nuestras cabezas. De alguna manera, existe una melodía incluso si nadie está interpretando una canción.

Si en todos los ejemplos dados por mí y en todos los ejemplos que puedo dar, y que serán intuitivamente claros para usted, el campo describe la propiedad, entonces, ¿cómo puede existir un campo sin un entorno? Pero de alguna manera los campos son independientes de su entorno, ya que muchos campos diferentes pueden comportarse de la misma manera, a pesar de que describen muchas propiedades diferentes de entornos completamente diferentes. Por lo tanto, es posible abstraer el campo del entorno.

De hecho, esto no solo es posible, sino que parece ser necesario. Como mínimo, es necesario no tener un medio o tener un entorno que no se pueda crear a partir de la materia ordinaria, que es fundamentalmente diferente de todos los medios considerados por nosotros, ya que funciona de tal manera (de acuerdo con todos los experimentos) que no existe .

Uno de varios elementos radicales de la teoría especial de la relatividad de Einstein de 1905 fue la idea de que para las ondas de luz, durante décadas consideradas ondas en campos eléctricos y magnéticos (ondas electromagnéticas), y moviéndose a la misma velocidad en el espacio vacío, no hay medio. Solo hay campos.

El medio hipotético se llamaba "éter"; Einstein argumentó que tal cosa no existe, y escribió un conjunto de ecuaciones para las cuales no era necesario. Observo que todavía hay un debate (a menudo más filosófico que físico) sobre si es necesario o no imaginar la existencia de un entorno extraño que es muy diferente de la materia ordinaria. Hasta la fecha, no hay evidencia que requiera su disponibilidad.

Los elementos clave de la versión de la relatividad de Einstein (en contraste con las versiones de Galileo y Newton) fueron los siguientes:

• El espacio y el tiempo no son lo que piensas que son. Los diferentes observadores que se mueven uniformemente entre sí divergirán en sus estimaciones de la longitud de los objetos y los intervalos de tiempo entre eventos (y estas discrepancias se pueden medir con precisión).
• Existe un límite de velocidad universal, s; cualquier observador que mida la velocidad de un objeto con respecto a él encontrará que esta velocidad es menor o igual a s.
• En un mundo así, ciertos campos - "campos relativistas" - pueden existir sin un medio, y satisfacen ecuaciones especiales de movimiento. El campo relativista más simple satisface las ecuaciones de movimiento de las clases 0 o 1, con la velocidad de onda cw mencionada en la ecuación de movimiento tomando el valor c.

En resumen, hay campos relativistas de clase 0 que satisfacen la ecuación.

$$

$$Clase 0: \; d ^ 2Z / dt ^ 2 - c ^ 2 d ^ 2Z / dx ^ 2 = 0$$

La luz, y todas las ondas electromagnéticas, es el ejemplo más famoso, pero no único, por lo tanto, "c" a menudo se llama "velocidad de la luz". Y hay campos relativistas de clase 1 que satisfacen la ecuación

$$

$$Clase 1: \; d ^ 2Z / dt ^ 2 - c ^ 2 d ^ 2Z / dx ^ 2 = - (2 \ pi \ mu) ^ 2 (Z - Z_0)$$

Veremos sus ejemplos en el próximo artículo. Tenga en cuenta que la relatividad no impone restricciones en μ (excepto por la necesidad de que μ ² sea ​​positivo) o en Z ₀ . Para los campos relativistas, existen ecuaciones más complejas, pero la mayoría de ellas en la descripción de procesos físicos simples se reducen a una de estas dos.

Los campos relativistas son físicamente reales y tienen un significado físico en el Universo, es decir:

• Sus olas transportan energía e información de un lugar a otro.
• Las ondas en un campo pueden afectar a otro campo y cambiar los procesos físicos que tendrían lugar en su ausencia.

Pero, a diferencia de los campos, cuyos ejemplos se dan en este artículo, los campos relativistas no describen la propiedad de ningún medio físico ordinario, que consiste en algo parecido a la materia ordinaria, y, hasta donde se sabe experimentalmente, no describen las propiedades de nada no importa que Estos campos, tal vez, hasta donde sabemos hoy, son uno de los elementos fundamentales del Universo.