Entendemos la física de partículas: 7) las partículas son cuantos

1. Bola sobre un resorte, versión newtoniana
2. Una bola cuántica en un resorte.
3. Olas, aspecto clásico
4. Ondas, la ecuación clásica del movimiento.
5. Ondas cuánticas
6. Campos
7. Las partículas son quanta
8. Cómo interactúan las partículas con los campos.

Entonces, finalmente, llegamos a nuestra meta: entender lo que esas cosas que llamamos "partículas" son, de hecho, electrones, fotones, quarks, gluones y neutrinos. Todo esto, por supuesto, se aplica a la ciencia moderna. Vale la pena recordar que en la ciencia no hay garantías de que la comprensión actual no se profundizará más.

El artículo anterior describía qué son los campos: objetos que tienen significado en cualquier punto del espacio y en cualquier momento del tiempo (funciones del espacio y el tiempo), satisfacen la ecuación de movimiento y son físicamente significativos en términos del hecho de que pueden transferir energía de un lugar a otro. e influir en los procesos físicos del universo.

Aprendimos que la mayoría de los campos que conocemos describen la propiedad de un medio, como la altura de una cuerda o la presión en un gas. Pero también aprendimos que en la teoría de la relatividad de Einstein hay una clase especial de campos, campos relativistas que no requieren un medio. O al menos si tienen un entorno, es muy inusual. Nada en las ecuaciones de campo requiere la presencia de ningún medio y no indica qué propiedad de este medio es descrita por los campos relativistas.

Entonces, por ahora, consideraremos los campos relativistas como objetos físicos elementales del universo, y no como ciertas propiedades de un medio desconocido. Si ese punto de vista será apoyado entre los físicos más adelante, el tiempo lo dirá.

Consideramos dos clases de campos relativistas, y ahora los estudiaremos con más detalle. O bien satisfacen la ecuación de movimiento de Clase 0, donde c _w = c (donde c es el límite de velocidad universal, a menudo llamado "velocidad de la luz").

$$

$$d ^ 2Z / dt ^ 2 - c ^ 2 d ^ 2Z / dx ^ 2 = 0$$

O ecuaciones de movimiento de clase 1, donde cw = c

$$

$$d ^ 2Z / dt ^ 2 - c ^ 2 d ^ 2Z / dx ^ 2 = - (2 \ pi \ mu) ^ 2 (Z - Z_0)$$

En el artículo anterior se demostró que μ es la frecuencia de onda mínima en dichos campos. En este artículo lo denotaremos por ν _min .

¿Por qué el límite de velocidad universal a menudo se llama la velocidad de la luz? Las ondas con una ecuación de clase 0 se mueven con velocidad c _w . La luz (un término general que denota ondas electromagnéticas de cualquier frecuencia) que se mueve a través del espacio vacío satisface la ecuación relativista de la clase 0, por lo tanto, las ondas de luz (y las ondas de cualquier campo relativista que satisfaga la ecuación relativista de la clase 0) se mueven con velocidad c.

Además, en el mismo artículo vimos que si un campo de clase 1 tiene una onda con amplitud A, frecuencia ν, longitud de onda λ y estado de equilibrio Z ₀ , entonces la ecuación de movimiento requiere que la frecuencia y la longitud de onda estén relacionadas con μ = ν _{min que} aparece en las ecuaciones por la fórmula

$$

$$\ nu ^ 2 = (c / \ lambda) ^ 2 + \ mu ^ 2 = (c / \ lambda) ^ 2 + \ nu_ {min} ^ 2$$

Esta es una fórmula pitagórica: se puede representar, si se desea, en forma de triángulo, como en la Fig. 1. La frecuencia mínima de cualquier onda es ν _min , y la asignación ν = ν _min (y, por lo tanto, como λ → ∞) corresponde a la compresión del triángulo a una línea vertical (Fig. 1, abajo). También puede obtener una relación similar de la clase 0 haciendo μ = ν _min cero. Luego puedes extraer la raíz cuadrada y obtener

$$

$$\ nu = c / \ lambda$$

Este es un triángulo comprimido a una línea horizontal (Fig. 1, derecha). En este caso, la frecuencia mínima es cero. El campo puede fluctuar arbitrariamente lentamente.


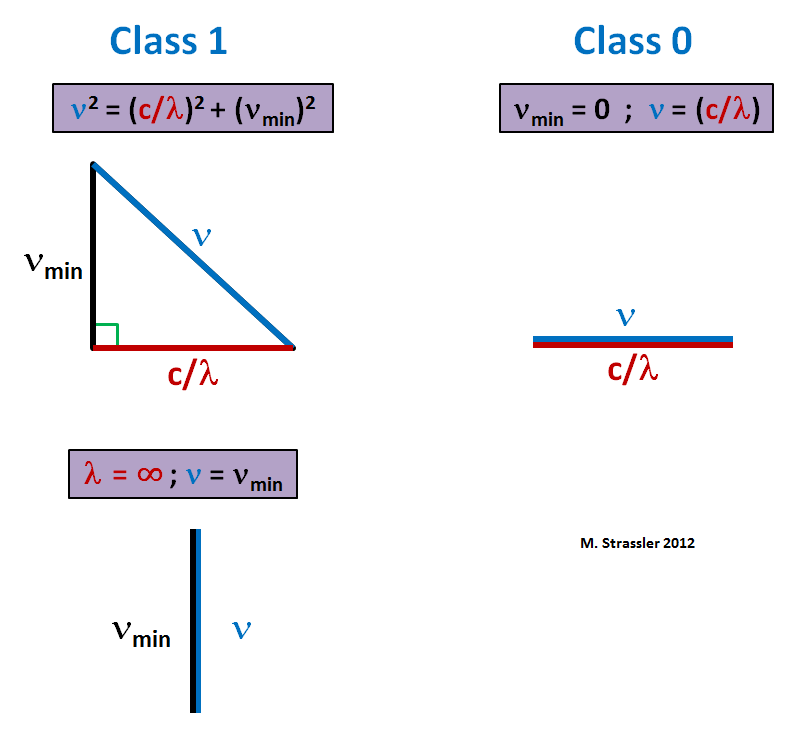Fig. 1

No hay restricciones sobre A. Pero esto se debe a que estamos ignorando la mecánica cuántica. Ha llegado el momento de estudiar campos cuánticos relativistas.

Campos cuánticos relativistas

El mundo real es de mecánica cuántica, por lo que la amplitud A no puede ser cualquiera. Toma valores discretos proporcionales a la raíz cuadrada de n, un número entero no negativo que indica el número de cuantos de vibración en la onda. La energía almacenada en la ola es

$$

$$E = (n + 1/2) h \ nu$$

Donde h es la constante de Planck, necesariamente aparece donde la mecánica cuántica importa. En otras palabras, la energía asociada con cada cuanto de oscilaciones depende solo de la frecuencia de las oscilaciones de la onda, y es igual a

$$

$$E = h \ nu$$

Esta relación fue propuesta por primera vez, específicamente para las ondas de luz, por Einstein en 1905, en su explicación del efecto fotoeléctrico.

Pero recordemos nuestra relación pitagórica de frecuencia y longitud de onda. Si lo multiplicamos por h ² , obtenemos eso para un campo cuántico de clase 1

$$

$$E ^ 2 = (h \ nu) ^ 2 = (h c / \ lambda) ^ 2 + (h \ nu_ {min}) ^ 2 \ quad (*)$$

Se ve familiar. Ya sabemos que cualquier objeto en la teoría de la relatividad de Einstein debe satisfacer la ecuación que describe su energía, momento y masa:

$$

$$E ^ 2 = (pc) ^ 2 + (mc ^ 2) ^ 2$$

Otra relación pitagórica. La energía mínima del objeto es mc ² , que se asemeja a la afirmación sobre la frecuencia mínima que puede poseer una onda de clase 1, ν _min . Podemos sentir la tentación de asumir que, probablemente, para un cuanto de un campo relativista

$$

$$p c = h c / \ lambda \ quad (**)$$

$$

$$m c ^ 2 = h \ nu_ {min} \ quad (***)$$

La primera ecuación apareció por primera vez en el trabajo de Louis De Broglie en 1924, casi 20 años después de Einstein. ¿Por qué tardó tanto? No lo se


Fig. 2

¿Tiene esto sentido? Como notamos, los campos relativistas de clase 0 también incluyen campos eléctricos, y sus ondas son ondas electromagnéticas, es decir, luz. La versión de la fórmula (*) que obtenemos para los cuantos de clase 0 es la misma que para los campos de clase 1 para los cuales μ = ν _{min es} igual a cero, es decir, m = 0. Extraemos la raíz cuadrada y obtenemos

$$

$$E = p c$$

O la ecuación de Einstein para partículas sin masa. Y los cuantos de ondas electromagnéticas (incluidos todos los tipos de luz: visible, ultravioleta, infrarroja, ondas de radio, radiación gamma, etc., que difieren solo en frecuencia y, por lo tanto, la energía de los cuantos) realmente serán partículas sin masa, tan pronto como apliquemos lo indicado arriba un par de ecuaciones (**) y (***). Estos son los fotones.

De la ecuación (***) finalmente podemos calcular la masa de la partícula. Cada partícula que tiene una masa es un cuanto de un campo de clase 1. La frecuencia mínima de tales ondas es ν _min . La energía mínima de un cuanto de dicha onda es igual a h veces la frecuencia. Y la masa de la partícula es simplemente la energía mínima dividida por c ² .

$$

$$m = h \ nu_ {min} / c ^ 2$$

Si queremos entender de dónde proviene la masa de partículas, debemos entender qué determina ν _min y por qué hay una frecuencia mínima en general. Para partículas como electrones y quarks, esto no está completamente claro, pero se sabe que el campo de Higgs juega un papel importante en esto.

Concluimos: las partículas de la naturaleza son cuantos de campos cuánticos relativistas. Las partículas sin masa son cuantos de ondas de campo que satisfacen una ecuación de clase 0. Los que poseen masa corresponden a los campos de una ecuación de clase 1. Hay muchos detalles, pero este hecho es una de las propiedades fundamentales básicas de nuestro mundo.

¿Estos cuantos realmente se comportan como partículas?

Imaginamos partículas como partículas de polvo o granos de arena. En este sentido, los cuantos no son partículas, son ondas que tienen una energía y amplitud mínimas para una determinada frecuencia. Pero se comportan tanto como partículas que se nos puede perdonar por usar la palabra "partícula" en su descripción. A ver por qué.

Si levanta una ola en el agua y la deja pasar a través de piedras poco profundas debajo de la superficie, parte de la ola cruzará la línea de piedras y parte se reflejará, como se muestra en la Fig. 3. La parte de la ola que cruzará la línea depende de la forma de las piedras, su proximidad a la superficie, etc. Pero la conclusión es que parte de la onda se transmite a través de las piedras, y parte se reflejará. Parte de la energía de las olas irá en la misma dirección, parte irá en la dirección opuesta.


Fig. 3

Pero si envía un fotón hacia el vidrio reflectante, este fotón lo atravesará o se reflejará (Fig. 4). Más precisamente, si mide el comportamiento de un fotón, descubrirá si se refleja o se transmite. Si no mide, será imposible decir qué sucedió. Bienvenido al pantano de la mecánica cuántica. Un fotón es un cuanto. Su energía no se puede dividir en la parte que pasó a través del vidrio y la parte que se reflejó, porque entonces en cada lado habrá menos de un cuanto, lo cual está prohibido. (Letra pequeña: el vidrio no cambia la frecuencia de los fotones, por lo que la energía no puede dividirse entre dos o más cuantos de frecuencias más bajas). Entonces el fotón, aunque es una onda, se comporta como una partícula en este caso. O bien se refleja en el cristal o no. Ya sea que se refleje o no, la mecánica cuántica no predice esto. Solo da la probabilidad de reflexión. Pero ella predice que pase lo que pase, el fotón viajará como una unidad y mantendrá su identidad.


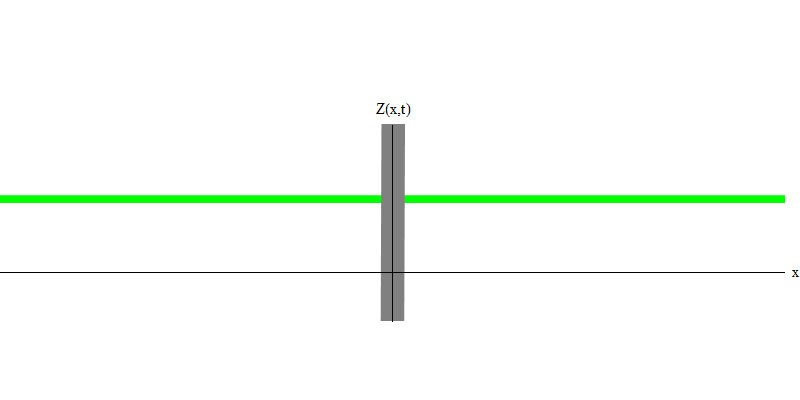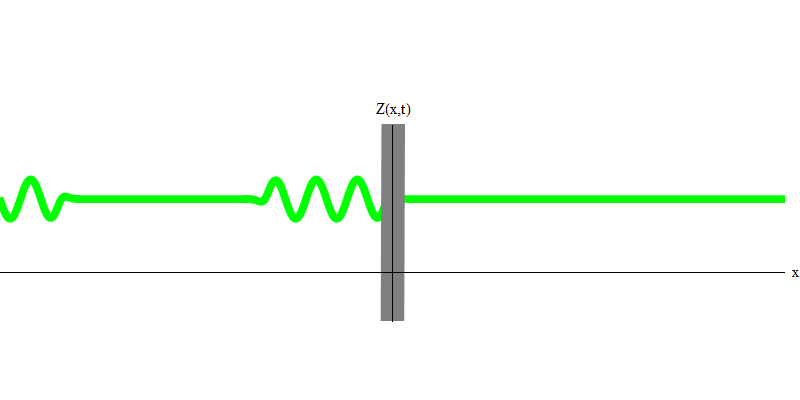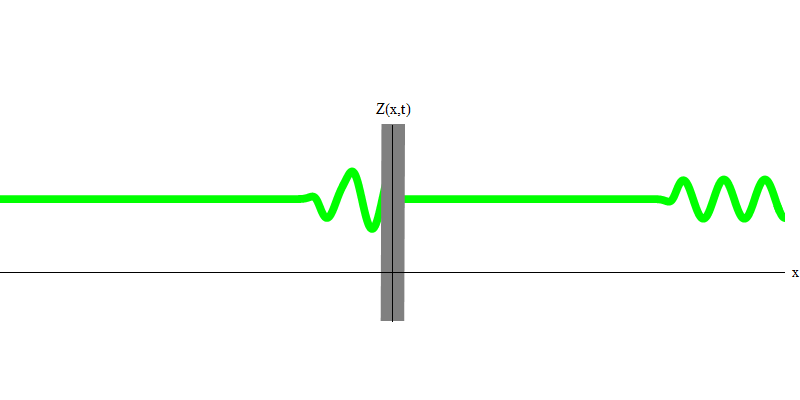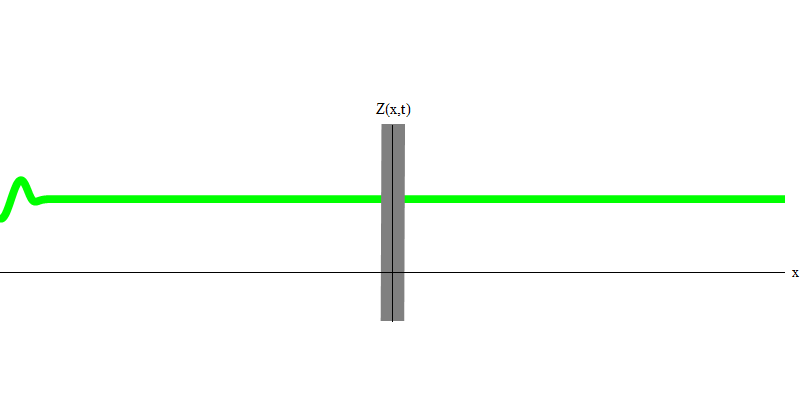Fig. 4 4

¿Y qué pasará con los dos fotones? Depende Por ejemplo, si los fotones se emiten en diferentes momentos desde diferentes lugares, entonces el observador verá dos cuantos, separados en el espacio y probablemente moviéndose en diferentes direcciones (Fig. 5). Pueden tener diferentes frecuencias.


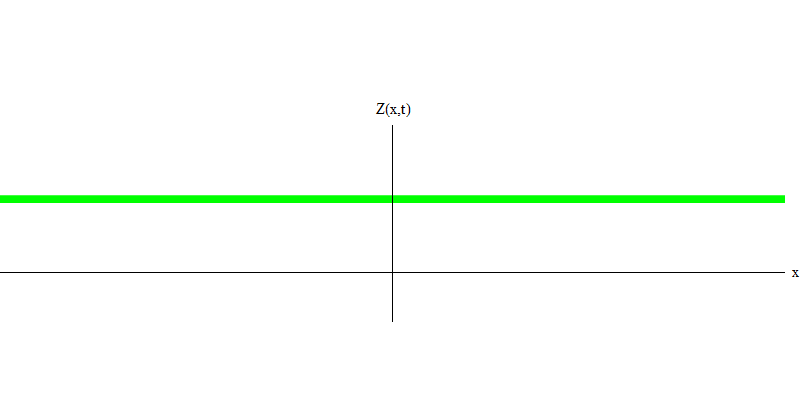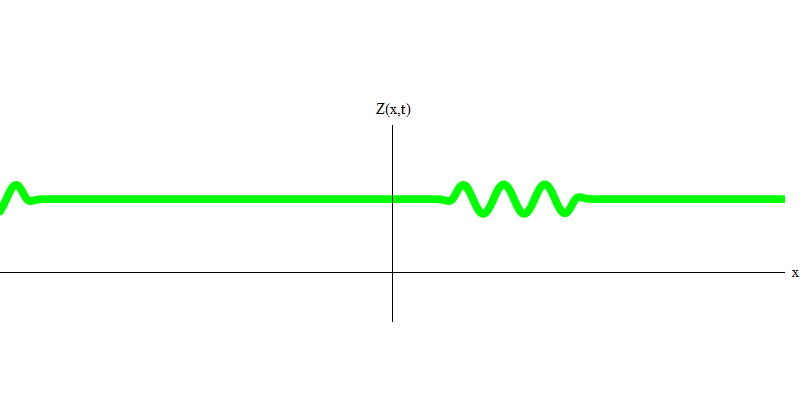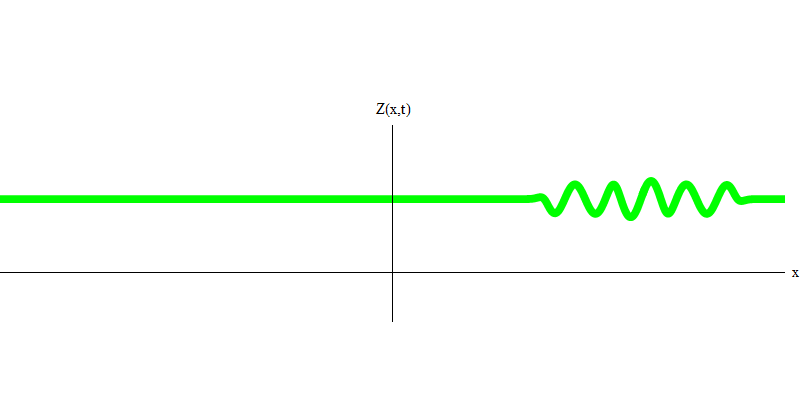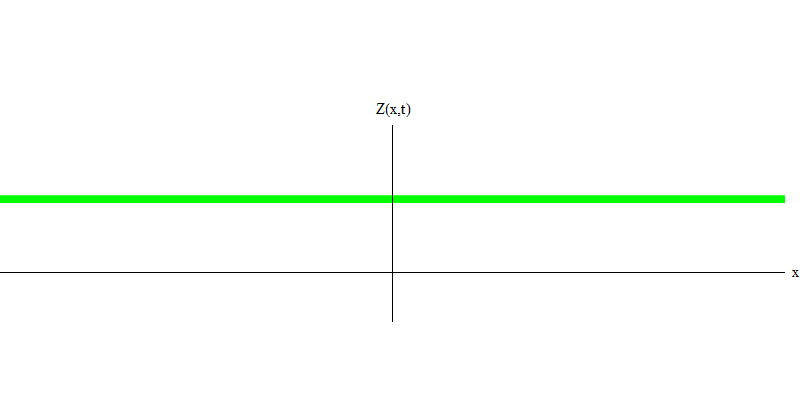Fig. 5: cuantos independientes

En el caso especial, cuando dos fotones se emiten juntos y perfectamente sincronizados (como en los láseres), se comportan como se muestra en la Fig. 6. Si enviamos una combinación de dos fotones al vidrio, entonces no pueden suceder dos, sino tres cosas. O ambos fotones pasarán a través del vidrio, o ambos se reflejarán, o uno pasará, y el otro se reflejará. 0, 1 o 2 fotones se reflejarán desde el cristal; no hay otras opciones. En este sentido, los cuantos de luz nuevamente se comportan como partículas, como bolas pequeñas: si arrojas dos bolas en una cuadrícula que tiene agujeros, entonces 0, 1 o 2 bolas se reflejarán desde la cuadrícula, y 0, 1 o 2 bolas pasarán por los agujeros . No hay posibilidad de que 1,538 goles se reflejen desde la red.


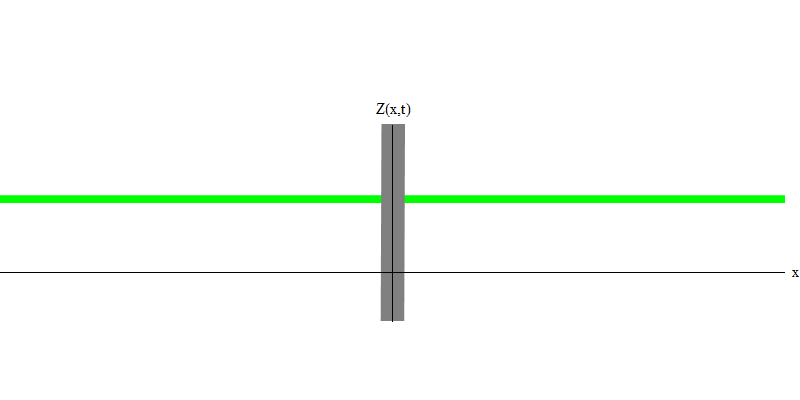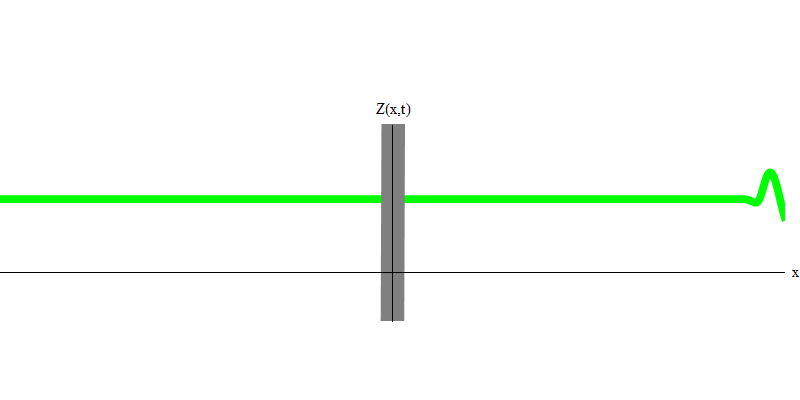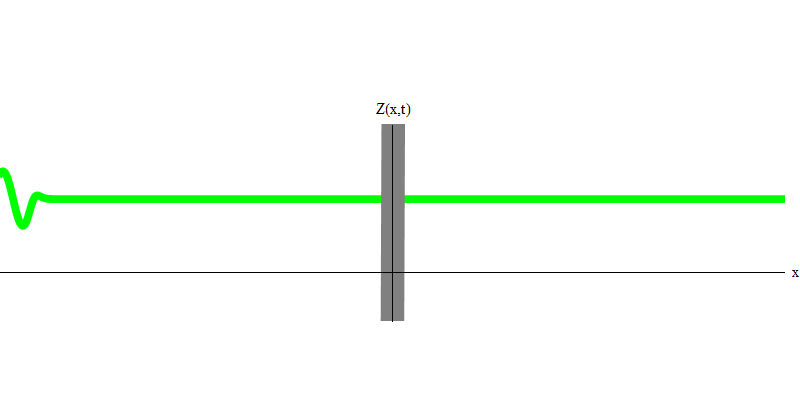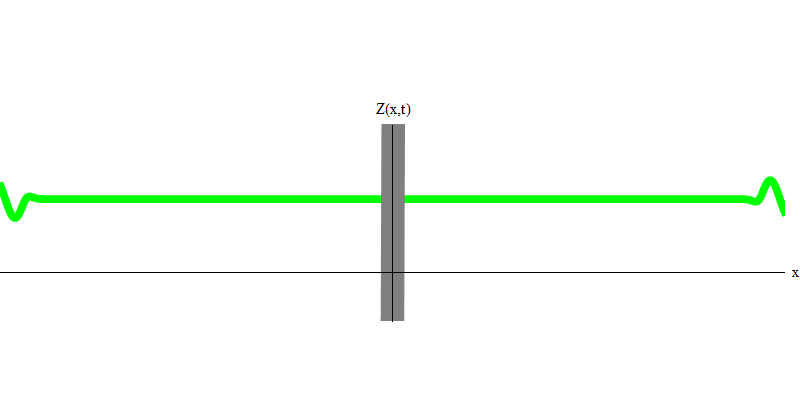Fig. 6 6

Pero estos son fotones que, sin masa, están obligados a moverse a la velocidad de la luz y E = p c. ¿Qué pasa con las partículas con masa como los electrones? Los electrones son cuantos del campo eléctrico y, como los fotones, pueden ser emitidos, absorbidos, reflejados o transmitidos como un todo. Tienen cierta energía e impulso, $$$E ^ 2 = (pc) ^ 2 + (m_e c ^ 2) ^ 2$donde m _e es la masa del electrón. La diferencia entre electrones y fotones es que se mueven más lentamente que la luz y, por lo tanto, pueden descansar. El bosquejo de tal evento (en mecánica cuántica, debido al principio de incertidumbre, nada puede ser verdaderamente estático) de un electrón estacionario se da en la Fig. 7. Esta es una onda de frecuencia mínima obtenida asignando una longitud de onda de un valor muy grande, casi infinito. Por lo tanto, la forma de onda espacial en la Fig. no muestra ninguna convolución, solo fluctúa en el tiempo.


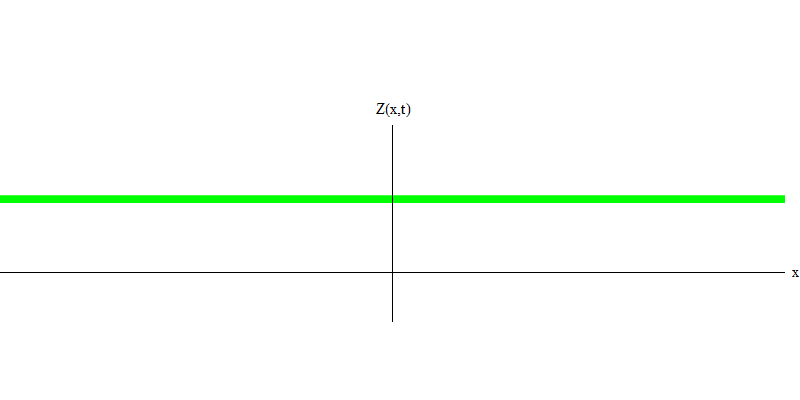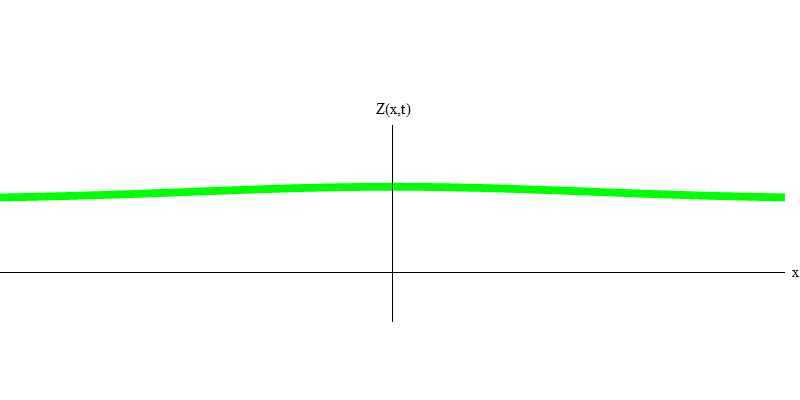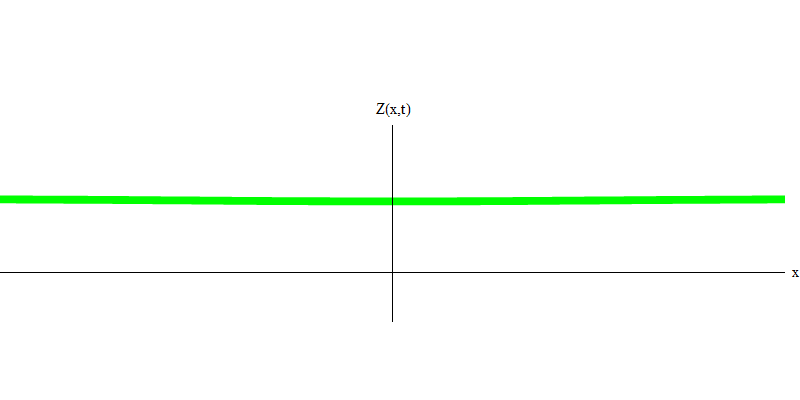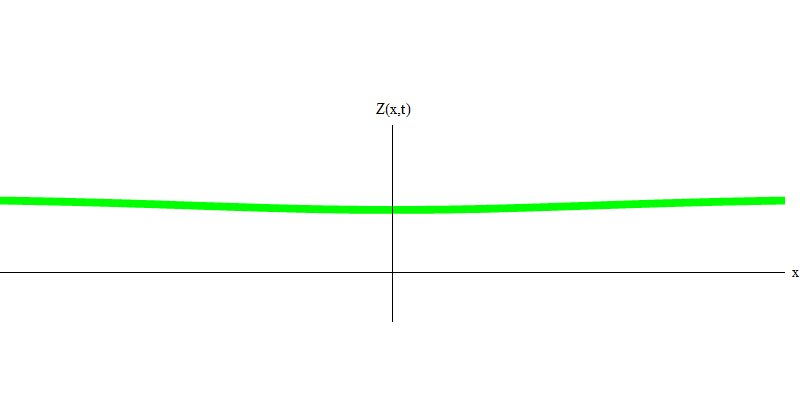Fig. 7 7

Entonces, sí, de hecho, los cuantos se comportan de manera muy parecida a las partículas y, por lo tanto, llamar "partículas" a electrones, quarks, neutrinos, fotones, gluones, partículas W y partículas de Higgs no será un engaño catastrófico. Pero la palabra "cuántico" es más adecuada para esto, porque estos son precisamente quanta.

¿En qué se diferencian los fermiones y los bosones entre sí?

• Todas las partículas elementales se dividen en fermiones y bosones.
• Los fermiones (incluidos los electrones, los quarks y los neutrinos) satisfacen el principio de exclusión de Pauli : dos fermiones del mismo tipo no pueden hacer lo mismo.
• Los bosones (incluidos fotones, partículas W y Z, gluones, gravitones y partículas de Higgs) son diferentes: dos o más bosones del mismo tipo pueden hacer lo mismo.

Es por eso que los láseres pueden estar hechos de fotones, ya que son bosones, pueden estar en el mismo estado y generar un poderoso rayo de una luz. Pero un láser no puede estar hecho de electrones que sean fermiones.

¿Cómo se manifiesta esta diferencia en el lenguaje de las matemáticas? Resulta que las fórmulas que traigo son adecuadas para los bosones, y para los fermiones deben cambiarse, ligeramente, pero con grandes consecuencias. Para los bosones tendremos:

$$

$$E = (n + 1/2) h \ nu, \ quad donde \; n = 0, 1, 2, 3, 4, ...$$

Lo que significa que la energía de cada cuanto es igual a h ν. Esto implica que los bosones quanta pueden hacer lo mismo; cuando n es mayor que 1, la onda en el campo bosónico consistirá en varios cuantos oscilando y moviéndose juntos. Pero para fermiones:

$$

$$E = (n - 1/2) h \ nu, \ quad donde \; n = 0 \; o \; 1$$

La energía de un cuanto es igual a h ν, por lo que toda la discusión de las partículas y sus energías, momento y masas sigue siendo válida. Pero el número de cuantos en una onda de electrones puede ser solo 0 o 1. Diez electrones, a diferencia de diez fotones, no pueden organizarse en una onda de mayor amplitud. Por lo tanto, no hay ondas de fermiones que consisten en una gran cantidad de fermiones, que oscilan y se mueven juntas.