
La teoría de cuerdas a menudo se llama la "teoría de todo" porque su propósito es describir todas las fuerzas fundamentales de interacción en el universo, incluyendo la gravedad, la mecánica cuántica y la teoría de la relatividad. Este concepto revolucionario introduce una nueva comprensión del espacio y el tiempo; busca explicar la conexión entre fenómenos como los agujeros negros y el plasma de quark-gluón, dimensiones adicionales y fluctuaciones cuánticas.
A pesar de la complejidad del tema en consideración, el profesor de la Universidad de Princeton Stephen Gabser ofrece una introducción espaciosa, asequible y entretenida a esta una de las áreas de física más discutidas en la actualidad. Con un mínimo de matemáticas, utilizando analogías interesantes, el autor explica la esencia de la supersimetría, la dualidad y la curvatura del espacio-tiempo para que quede claro para cualquier lector con una gran cantidad de conocimientos de la escuela secundaria.
Si bien las disposiciones de la teoría de cuerdas no se han demostrado de manera concluyente, esos secretos que ya nos han sido revelados nos permiten admirar la armonía armoniosa del universo y discutir la aplicación práctica de futuros descubrimientos en la física de alta energía.
Gravedad versus mecánica cuántica
La mecánica cuántica y la relatividad general, las dos teorías físicas triunfales que surgieron a principios del siglo XX, resultaron ser inconsistentes entre sí. La dificultad surge cuando se aplica el método llamado renormalización. Hablaré sobre la renormalización usando el ejemplo de fotones y gravitones, del cual ya hablamos en capítulos anteriores. La esencia de la inconsistencia es que los fotones nos llevan a una teoría renormalizable (que significa: "buena teoría"), mientras que los gravitones conducen a una teoría no renormalizable, y esto en realidad significa que no tenemos una teoría general que describa fotones y gravitones.
Los fotones interactúan con las cargas eléctricas, pero ellos mismos son eléctricamente neutros. Por ejemplo, un electrón que tiene una carga eléctrica en un átomo de hidrógeno, saltando de un nivel de energía a otro, emite un fotón. Esto es exactamente lo que quiero decir cuando digo que los fotones interactúan con las cargas. La afirmación de que el fotón en sí no tiene una carga eléctrica equivale a la afirmación de que la luz no conduce electricidad. Si esto no fuera así, entonces recibirías una descarga eléctrica cada vez, agarrándote a un objeto que había estado expuesto a la luz del sol durante el tiempo suficiente. Los fotones no interactúan entre sí; solo interactúan con cargas eléctricas.
Los gravitones no responden a las cargas, sino a la masa, la energía y el impulso. Y dado que transfieren energía, también interactúan entre sí. Puede parecer que esto no presenta un problema particular, pero es precisamente por esto que encontramos dificultades. La mecánica cuántica nos enseña que los gravitones se comportan como ondas y como partículas. Las partículas son hipotéticamente objetos puntuales. Y el gravitón puntual lo atraerá cuanto más fuerte, más cerca se acerque. Su campo gravitacional se puede describir como la emisión de otros gravitones. Llamaremos al gravitón de prueba materno, y los gravitones emitidos por él: hija. El campo gravitacional cerca del gravitón madre es muy fuerte. Entonces, los gravitones de su hija tienen enormes energías y momentos. Esto se deduce directamente del principio de incertidumbre: los gravitones hijos se observan a una distancia muy pequeña Δx del gravitón original y, por lo tanto, de acuerdo con la relación de incertidumbre, Δp × Δx ≥ h / 4π, su incertidumbre de momento, Δp, es muy grande. El problema es que los gravitones también son sensibles al impulso. Los gravitones hijos mismos emitirán gravitones. Todo el proceso se ramifica y diverge increíblemente rápido: no se pueden tener en cuenta todas las consecuencias de la interacción de todos los gravitones.
De hecho, algo similar sucede cerca del electrón. Si intenta medir el campo eléctrico muy cerca del electrón, provoque que emita un fotón con un impulso muy grande. Esto parece inofensivo porque, como sabemos, los fotones no emiten otros fotones. El problema es que un fotón puede dar a luz un par electrón-positrón, que luego emite aún más fotones que generarán nuevos electrones y positrones ... ¡Un desastre completo! Lo más sorprendente es que, en el caso de los electrones y fotones, sin embargo, puede describir completamente toda la multitud de partículas en cascada entre sí. A veces hablan de ropa, o "abrigos de piel", de la descendencia en la que se envuelve un electrón. Los físicos usan el término "partículas virtuales" para describir la progenie electrónica. La renormalización es un método matemático que le permite rastrear todo este desastre.
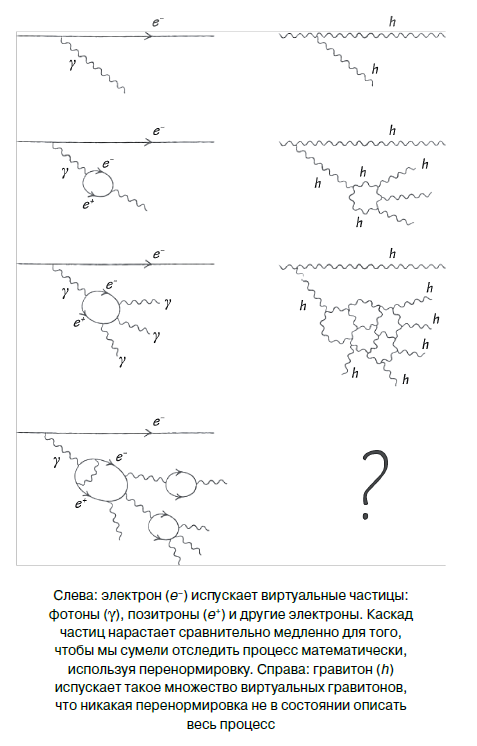
La idea de la renormalización es que se supone que un electrón "desnudo" tiene carga infinita y masa infinita, pero tan pronto como "vestimos" un electrón, su carga y masa adquieren valores finitos.
El problema con los gravitones es que no podemos renormalizar la nube de gravitones virtuales que lo rodean. La teoría general de la relatividad, la teoría de la gravedad, no es renormalizable. Esto puede parecer un problema técnico confuso: hay pocas posibilidades de que simplemente estemos viendo el problema desde el lado equivocado. También hay una posibilidad aún más débil de que una teoría llamada Teoría de la supergravedad máxima sea renormalizable. Sin embargo, yo y la mayoría de los teóricos de cuerdas estamos convencidos de que existen dificultades fundamentales para combinar la mecánica cuántica y la gravedad.
Ahora tomemos la teoría de cuerdas. La suposición inicial subyacente es que las partículas no son partículas puntuales. En cambio, las partículas se representan como modos vibracionales de una cuerda. Según la idea generalmente aceptada de la teoría de cuerdas, las cuerdas son objetos que son infinitamente delgados, pero que tienen una longitud finita (del orden de 10–34 metros), interactuando entre sí en forma de gravitones. Stop stop! - Tú protestas. "¿Pero es que en este caso, los problemas generales con una nube de partículas virtuales, en este caso, cadenas virtuales, no nos llevarán a la misma imposibilidad de rastrear todo el proceso de interacción, como en el caso de los gravitones?" No El hecho de que las cadenas no sean objetos puntuales mata el problema descrito de raíz. La fuente de dificultad en el caso de los gravitones es la suposición de que, de acuerdo con el término "partícula puntual", son infinitamente pequeños. Reemplazar los gravitones con cuerdas vibratorias suaviza los "ángulos agudos" de su interacción entre ellos. “En los dedos” esto puede explicarse de la siguiente manera: cuando el gravitón da lugar a otro gravitón virtual, puede indicar con precisión el lugar y la hora en que sucedió esto. Pero cuando la cadena se ramifica, parece una rama de una tubería de agua.
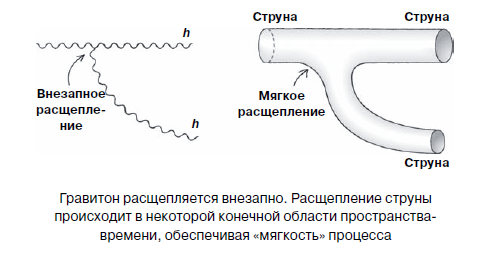
En el punto de ramificación no hay un punto en el que se produzca una ruptura, la figura en forma de Y que ilustra este proceso parece un segmento de tubería continuo y liso, solo que tiene una forma inusual. Todo esto lleva al hecho de que la división de la cuerda es un proceso más "suave" que la división de la partícula. Los físicos dicen que las cuerdas interactúan por naturaleza "suavemente", mientras que las partículas interactúan por naturaleza "duramente". Es esta suavidad la que proporciona el mejor comportamiento de la teoría de cuerdas que la teoría general de la relatividad, en relación con la aplicabilidad de la descripción mecánica cuántica.
Cuerdas en el espacio-tiempo
Recordemos brevemente de qué estábamos hablando las vibraciones de la cuerda del piano. Si tira de la cuerda entre dos clavijas y la golpea con un martillo, vibrará con cierta frecuencia. La frecuencia es el número de oscilaciones por segundo. Además de la frecuencia principal, la cuerda del piano también vibra en armónicos, que son vibraciones de frecuencias más altas que le dan al sonido del piano un color característico. Cité esta analogía cuando describí el comportamiento de un electrón en un átomo de hidrógeno: también tiene un modo vibratorio fundamental que corresponde al estado fundamental con energía mínima, y modos adicionales que corresponden a niveles de energía más altos.
La analogía descrita puede no satisfacerte por completo: "Bueno, ¿qué tiene que ver el electrón en el átomo de hidrógeno con la onda estacionaria en la cuerda del piano?" - usted pregunta La mayoría está más cerca de la analogía con el planetoide infinitamente pequeño que gira en órbita alrededor del pequeño sol: el núcleo atómico, ¿no? ¿Es buena esa analogía? Si y no La mecánica cuántica afirma que la idea de un electrón como partícula y la idea de un electrón como onda están tan profundamente entrelazadas que el movimiento mecánico cuántico de una partícula de electrones alrededor de un protón puede describirse realmente como una onda estacionaria.
Comparar una cuerda de piano con las cuerdas que aparecen en la teoría de cuerdas es en realidad un método muy correcto. Para evitar confusiones con diferentes tipos de cadenas, llamaré a esas cadenas que la teoría de cuerdas trata con "cadenas relativistas". Este término tiene un significado didáctico muy profundo, porque la teoría de cuerdas incluye la teoría de la relatividad, tanto especial como general. Ahora quiero hablar sobre una construcción de la teoría de cuerdas que se parece tanto a una cuerda de piano como una cuerda puede ser incluso como una cuerda. Las cadenas relativistas pueden terminar en objetos llamados D-branes. Si omitimos los efectos asociados con la interacción de las cadenas, entonces las D-branas pueden considerarse infinitamente pesadas. Los detalles sobre D-branes se discutirán en el próximo capítulo, y ahora haré solo una pequeña digresión, por así decirlo, como una "muleta". La D-brane más simple se llama D0-brane (se pronuncia "brane de-zero"). Esta es una partícula puntual. Ya puedo escuchar la indignación de algunos lectores sobre el retorno a las partículas puntuales: "¿No ha declarado recientemente el autor que la teoría de cuerdas tiene como objetivo eliminar las partículas puntuales?" Bueno, sí, eso fue hasta mediados de la década de 1990, y luego las partículas puntuales volvieron a la teoría de cuerdas, y no solo, sino que condujeron a un zoológico completo de animales desconocidos. Pero me estoy adelantando a mí mismo. Todo lo que quiero hacer es dar el análogo teórico de cuerdas de las clavijas de piano que sostienen la cuerda en un estado tenso, y las branas D0 son tan apropiadas en este papel que no puedo resistirme a contarlas. En resumen, tiramos de la cuerda relativista entre dos branas D0, como una cuerda de piano entre dos clavijas. Las propias branas D0 no están unidas a nada, pero permanecen inmóviles porque tienen una masa infinita. Gracioso, ¿no es así? Entonces está bien. Sobre D0-branes, en el próximo capítulo, y ahora, solo sobre una cuerda estirada.
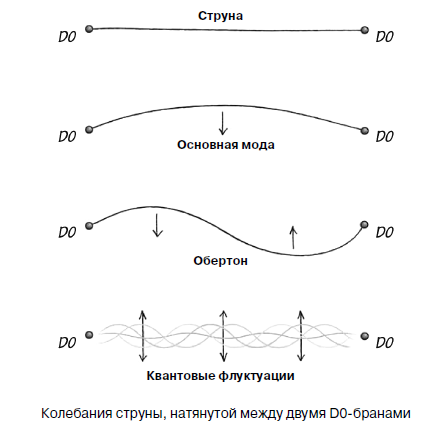
El nivel de energía más bajo de una cuerda estirada corresponde a la ausencia de vibraciones. Bueno ... casi ausente, porque las pequeñas oscilaciones cuánticas siempre están presentes, y este hecho es importante. Es muy correcto imaginar que el nivel de energía más bajo tiene una pequeña energía vibratoria dentro del marco de lo que permite la mecánica cuántica. Los niveles excitados de la cuerda relativista corresponden a sus oscilaciones, ya sea en la frecuencia fundamental o sobretonos de la frecuencia fundamental, y también puede vibrar en varias frecuencias simultáneamente, al igual que una cuerda de piano. Pero, al igual que un electrón en un átomo de hidrógeno, una cadena relativista no puede vibrar a una frecuencia arbitraria. Un electrón puede seleccionar niveles de energía de un conjunto discreto. Las cadenas relativistas son exactamente iguales. Los diferentes niveles vibratorios tienen diferentes energías, y dado que la masa y la energía están relacionadas por la relación E = mc2, las diferentes masas corresponden a diferentes estados vibratorios.
Sería genial si pudiera decir que la frecuencia de vibración de una cuerda está relacionada con su energía por una relación simple del tipo E = hν, como fue el caso de los fotones. Lamentablemente, esto no es tan simple. La masa total de la cuerda se compone de varios componentes. El primero de ellos es la masa en reposo de la cuerda, que corresponde a la energía de tensión de la cuerda entre dos branas D0. La segunda es la masa correspondiente a la energía vibracional, que a su vez consiste en las energías vibracionales de todos los armónicos. Recuerde que la energía y la masa están relacionadas por la relación E = mc2. Y finalmente, el tercer componente es la masa correspondiente a la energía de fluctuaciones cuánticas irrecuperables, llamadas oscilaciones de punto cero. El término "vibraciones cero" nos hace recordar la inevitabilidad fundamental de las fluctuaciones cuánticas. Entonces: la contribución de la energía de punto cero a la masa de la cuerda ... ¡es negativa! Estoy de acuerdo, esto es extraño. Muy extraño Para mostrar lo extraño que es esto, daré un ejemplo. Si nos limitamos a un solo modo vibratorio de una cuerda, veremos que la energía de las vibraciones de punto cero de este modo es positiva. Cada uno de los armónicos más altos individualmente proporciona una contribución positiva aún mayor a la energía de la cuerda. Pero si sumamos adecuadamente las contribuciones de todos los armónicos, obtenemos un número negativo. Si crees que esto no es lo suficientemente malo, entonces estas son aún más malas noticias: oculté parte de la verdad al decir que la contribución de la energía de las vibraciones de punto cero es negativa. Todos estos efectos (masa en reposo, energía vibracional y energía vibratoria de punto cero) entran en la expresión de la masa total por los cuadrados de sus valores. Y si la energía de las vibraciones de punto cero prevalece en esta suma, entonces el cuadrado de la masa total es negativo, lo que significa que la masa misma es imaginaria, como la raíz de menos uno.
Antes de rechazar con indignación tales tonterías, permítanme agregar que, en la teoría de cuerdas, toda una línea de investigación se dedica a la eliminación del problema descrito. En pocas palabras, el problema es que el cuadrado de la masa de la cadena relativista en su estado de energía más bajo es negativo. Las cadenas en este estado se llaman taquiones. Sí, sí, estos son los mismos taquiones que en cada serie confrontan a los héroes de Star Trek. Esto definitivamente es una mala noticia. En el modelo que describí, sería posible deshacerse del cuadrado de masa negativa tirando de las branas D0 a las que están unidos los extremos de la cuerda, lo suficiente como para que la energía de tensión de la cuerda sea mayor que la energía de las vibraciones de punto cero. Pero cuando no hay branes D0 cerca, la cadena en sí misma permanece. Privado de la capacidad de apegarse a algo, puede encerrarse en sí mismo. Ahora ella no se estira entre algo y algo y puede fluctuar, pero tal vez no. Lo único que no puede dejar de hacer es fluctuar a nivel cuántico. Y, como antes, las oscilaciones cuánticas convierten dicha cuerda en un taquión, lo cual es muy, muy malo para la teoría. Según los conceptos modernos, los taquiones son inestables, son similares a un equilibrio de lápiz en la punta. Puede intentar equilibrar un lápiz de este tipo, pero cualquier respiración ligera lo volcará. La teoría de cuerdas que contiene taquiones se asemeja a una teoría que describe millones de lápices en el borde del espacio de relleno.
Sin embargo, he exagerado demasiado. Hay una solución de ahorro para taquiones. Suponga que el estado fundamental de una cadena de taquiones corresponde a la masa imaginaria y su cuadrado: m2 <0. La energía vibratoria también hace una cierta contribución al cuadrado de la masa. Usando el mazo correcto y entregando las cartas de la manera necesaria, puedes asegurarte de que la masa total de la cadena sea exactamente cero. Esto es alentador porque, como sabemos, en el mundo real hay partículas sin masa, como fotones o gravitones. Por lo tanto, si las cadenas realmente describen el mundo real, entonces deben estar sin masa o, más estrictamente, al menos algunos de los estados cuánticos de las cadenas deben estar sin masa.
Tenga en cuenta que debe tomar el mazo de cartas correcto. Con esta metáfora, quería decir que necesitamos un espacio-tiempo de 26 dimensiones. Es posible que ya hayas adivinado que todo vendrá a esta desgracia, así que no me disculparé. Hay varios argumentos a favor de 26 dimensiones, pero la mayoría de ellos son puramente matemáticos, y me temo que no parecerán convincentes para la mayoría de los lectores. El argumento que daré es más físico. Nos gustaría obtener estados cuánticos sin masa de las cadenas. Sabemos que las oscilaciones cuánticas cero "empujan" m2 en la dirección negativa. También sabemos que los modos de vibración "empujan" m2 en la dirección opuesta. El valor mínimo posible de la energía vibratoria no depende de la dimensión del espacio, mientras que la magnitud de las vibraciones cuánticas cero depende. Miremos desde este lado: cuando algo duda, una cuerda de piano u otra cosa, lo hace en cierta dirección. La cuerda del piano oscila en la dirección en que la golpeó el martillo; por ejemplo, una cuerda de piano oscila arriba y abajo, pero no a la derecha ni a la izquierda. El bamboleo selecciona una dirección e ignora el resto. Por el contrario, las vibraciones de punto cero de la mecánica cuántica se producen en todas las direcciones posibles, y la adición de cada nueva dimensión agrega fluctuaciones cuánticas en otra dirección en la que pueden ocurrir oscilaciones. Más direcciones posibles de oscilaciones, o, como se les llama, grados de libertad, significa un mayor número de fluctuaciones, lo que conduce a una mayor contribución negativa a m2. Solo queda calcular cómo elegir las contribuciones a la masa total de modos vibracionales y cero vibraciones. Resulta que un modo oscilatorio con un valor mínimo de energía se compensa con una oscilación cuántica de 26 dimensiones. ¡Mire esto con optimismo, porque el número de mediciones necesarias podría ser no integral! ¿Qué haríamos, por ejemplo, con veintiséis dimensiones y media?
Si no ha dominado los diferentes tipos de fluctuaciones, no se preocupe. Son muy parecidos. La única diferencia entre los modos vibratorios y las vibraciones cuánticas cero es que los modos vibratorios pueden o no estar presentes, mientras que las vibraciones cero siempre están presentes. Las vibraciones cero son esos movimientos mínimos, cuya presencia es requerida por el principio de incertidumbre. Además del modo principal, los armónicos están presentes en las vibraciones de la cuerda, lo que le da a la cuerda nuevas propiedades de mecánica cuántica. Prefiero imaginar varios modos en forma de modelos mecánicos simples, como vibraciones circulares, vibraciones en forma de hoja de trébol o vibraciones torsionales. . , . , , -. , . — - .
, : , . , , . . 26- . . , , , . .
, 26 10. , . - . --, , . . -- , « », . , , - ˆ, ˆ. , . - . — . - , .
, . . -, . , , , , . , , , , , , - , , , , . , . , - , , . . . , . — .
»Se puede encontrar más información sobre el libro en
el sitio web del editor»
Contenidos»
Extracto20% —