Entendemos la física de partículas: 8) cómo las partículas interactúan con los campos

Comprender la física de partículas:
1. Bola sobre un resorte, versión newtoniana
2. Una bola cuántica en un resorte.
3. Olas, aspecto clásico
4. Ondas, la ecuación clásica del movimiento.
5. Ondas cuánticas
6. Campos
7. Las partículas son quanta
8. Cómo interactúan las partículas con los campos.

Cómo funciona el campo de Higgs:
1. La idea principal

En un artículo anterior de la serie, expliqué que las partículas de la naturaleza son cuantos de campos relativistas que satisfacen las ecuaciones de movimiento de la clase 0 y la clase 1. Pero lo que no he dicho hasta ahora, por lo que esta afirmación, afortunadamente, solo es parcialmente cierta. Las ecuaciones reales siempre son un poco más complejas, de modo que la interconexión de partículas y campos permanece, pero se hacen posibles fenómenos y procesos mucho más diversos, incluida la aparición de partículas después de la colisión de otras partículas, la descomposición de partículas en otras partículas y la dispersión de partículas entre sí, así como la formación de objetos interesantes como protones y neutrones, núcleos atómicos y átomos. No podré explicar todo esto en detalle, pero en este artículo le daré una introducción sobre cómo funciona todo.

La diferencia clave entre las ecuaciones, que llamé "clase 0" y "clase 1", y las ecuaciones que son significativas para la física real, es que en las ecuaciones reales hay términos adicionales que dependen de dos o más campos, y no solo uno . Es decir, digamos, en lugar de una ecuación de clase 0 para un campo relativista Z (x, t), que se ve como

$$

$$d ^ 2Z / dt ^ 2 - c ^ 2 d ^ 2Z / dx ^ 2 = 0$$

para campos reales, las ecuaciones se parecen más a esto:

$$

$$d ^ 2Z / dt ^ 2 - c ^ 2 d ^ 2Z / dx ^ 2 = y ’Z (x, t) ^ 3 + y A (x, t) B (x, t)$$

Donde y e y 'son números (generalmente menos de 1), Z es una notación corta de Z (x, t), y A (x, t) y B (x, t) son un par de otros campos. En tales ecuaciones, uno puede esperar la aparición de términos como A (x, t) Z (x, t), o A (x, t) ² Z (x, t), o Z (x, t) ² , o incluso A (x, t) d ² Z / dt ² , etc. Qué miembros pueden y cuáles no pueden aparecer, depende de los detalles de los campos involucrados en el proceso. Las reglas son estrictas, pero bastante confusas, por lo que no entraremos en ellas por ahora. En general, a partir de experimentos establecimos (y entendimos desde un punto de vista teórico) que en la naturaleza:

• Cualquier término válido en principio (conservación de la carga eléctrica o correspondencia de la relatividad de Einstein) aparece en las ecuaciones,
• pero los miembros con muchos campos suelen ser muy pequeños e insignificantes en comparación con los miembros con uno, dos y, a veces, tres campos (los miembros con derivadas de tiempo o espacio también suelen ser pequeños).

Por lo tanto, en los procesos físicos más interesantes, uno puede enfocarse en todos los términos válidos con uno, dos o tres campos.

Un poco de terminología. Los términos en las ecuaciones con campos se denominan lineales en primer grado. Todos los términos en nuestra clase 0 o 1 ecuaciones fueron lineales. Los miembros con dos o tres campos se llaman cuadráticos o cúbicos; en general, se llaman no lineales. Todos los fenómenos interesantes de nuestro mundo aparecen debido a términos no lineales en las ecuaciones de movimiento, es decir, la interacción de los campos entre sí y con ellos mismos. Estudiemos uno de ellos.

El surgimiento de una nueva ola a partir de la resonancia de los otros dos.

Para tener una idea de lo interesante que puede llegar a ser todo, tomamos tres campos, A (x, t), B (x, t), C (x, t) y una situación simplificada. Suponga que los campos A y B satisfacen aproximadamente las ecuaciones de clase 0 (y contienen cuantos sin masa), y el campo C satisface las ecuaciones de clase 1 (contiene ondas con una frecuencia mínima ν _min , y, en consecuencia, cuantos con masa m = h ν _min / c ² , donde h - Constante de Planck). También agregaremos términos no lineales a sus ecuaciones. Específicamente, así (por brevedad, escribiremos "A" en lugar de "A (x, t)", y así sucesivamente, c es la velocidad de la luz, y es un número generalmente menor que 1):

$$

$$d ^ 2A / dt ^ 2 - c ^ 2 d ^ 2A / dx ^ 2 = y BC \\ d ^ 2B / dt ^ 2 - c ^ 2 d ^ 2B / dx ^ 2 = y AC \\ d ^ 2C / dt ^ 2 - c ^ 2 d ^ 2C / dx ^ 2 = (2 \ pi \ nu_ {min}) ^ 2 C + y AB$$

Letra pequeña: agregué términos no lineales a las tres ecuaciones porque la presencia de dichos términos en una de las ecuaciones y la ausencia de ellas en la otra generarán contradicciones; por ejemplo, la energía no se conservará. Para el proceso que estoy describiendo, necesitaremos considerar solo términos no lineales en las ecuaciones de movimiento del campo C.

Veamos qué sucede con tal conjunto de ecuaciones si la onda del campo A se encuentra con la onda del campo B. En principio, podemos adivinar esto aplicando el método de examen minucioso. Si hay una onda en el campo A, entonces A (x, t) no está cerca de cero. Cuando las ondas de los campos A y B se superponen, el resultado de multiplicar A (x, t) y B (x, t) se vuelve distinto de cero. Ahora pasamos a la ecuación para C: los cambios en el campo C en el tiempo y el espacio (dos términos en el lado izquierdo) están asociados con el producto A y B (uno de los términos en el lado derecho).

$$

$$d ^ 2C / dt ^ 2 - c ^ 2 d ^ 2C / dx ^ 2 = (2 \ pi \ nu_ {min}) ^ 2 C + y A B$$

Entonces, incluso si el campo C es cero cuando A (x, t) B (x, t) se convierte en no cero, entonces C (x, t) pronto se convertirá en no cero en la misma sección. En resumen, como resultado de la reunión de las ondas A y B, ocurrirá una pequeña perturbación del campo C.

Letra pequeña: puede interesarle: después de que C no sea cero, si el término A (x, t) C (x, t) se convierte en la ecuación de movimiento para el campo. Causa perturbación adicional del campo B. La respuesta es sí, pero este efecto será incluso más pequeño Hasta que lo ignoremos y luego descubramos por qué valió la pena hacerlo.

En la fig. La Figura 1 muestra una onda con una frecuencia ν en el campo A (verde), que ocurre con una onda de frecuencia ν en el campo B (azul). Ecualicé frecuencias para simplicidad y simetría. Más adelante veremos por qué otros casos se reducen a esto. La velocidad ν se puede estimar observando la onda verde y la línea vertical ubicada en un punto en el espacio y oscilando con la onda.

El producto naranja a continuación muestra el producto A (x, t) B (x, t); se ve que se vuelve distinto de cero cuando se superponen dos ondas. También se ve que varía en el tiempo. Puede ver (comparándolo con una barra vertical oscilante) que A (x, t) B (x, t) oscila el doble de rápido. Recuerda este hecho importante. En el caso general, si una onda de frecuencia ν _{1 se} encuentra con una onda de frecuencia ν ₂ , entonces su producto oscilará con una frecuencia ν ₁ + ν ₂ . Y una cosa más: puede notar que las vibraciones AB no se mueven hacia la derecha o hacia la izquierda, permanecen en su lugar. Más adelante veremos por qué esto es importante.


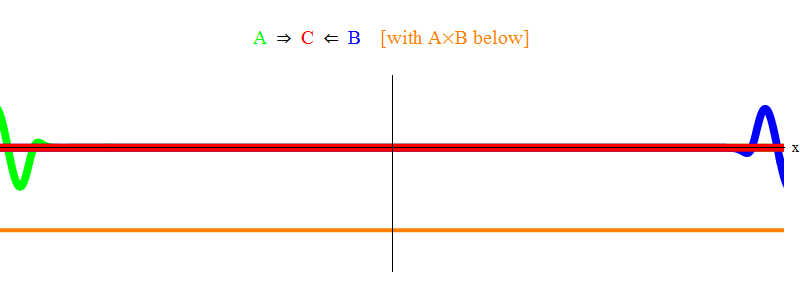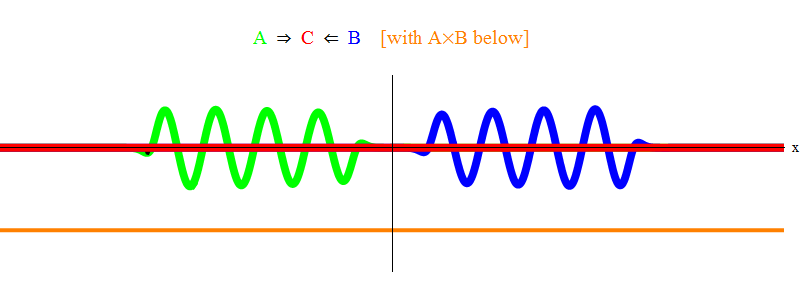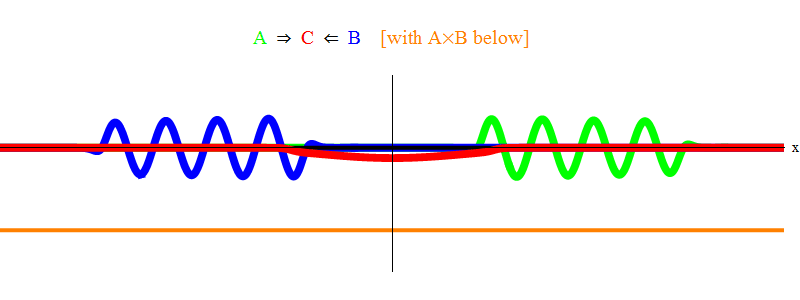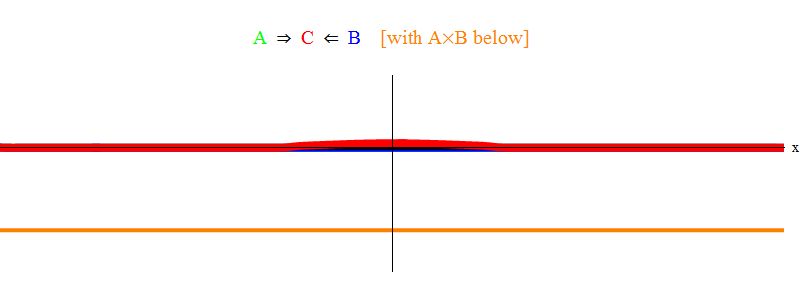Fig. 1

¿Cómo un valor distinto de cero de AB afecta a C? La respuesta depende en gran medida de la frecuencia ν. Primero le daré una respuesta lista, y luego una explicación aproximada de la razón. Esto es, de hecho, resonancia . La resonancia es un fenómeno integral de todas las vibraciones (vibraciones), incluidas las ondas. Ya he descrito cómo la bola en el resorte oscila con una frecuencia natural, y cómo la fuerza vibratoria que empuja la bola puede generar resonancia si la frecuencia de oscilación de la fuerza coincide con la frecuencia natural de la bola en el resorte.

Una vez que haya entendido la resonancia, verá que el campo C, que oscila con una frecuencia mínima y una velocidad horizontal cero, se comporta como una bola en un resorte, y AB se comporta como una fuerza oscilante que intenta hacer que la bola oscile. Por lo tanto, el fenómeno de resonancia ocurre si la frecuencia de vibración AB - 2ν - es la frecuencia mínima del campo C - ν _min . Más específicamente:

• Si 2 ν no es igual a ν _min - si la fuerza no está en resonancia - entonces en el área donde AB no es igual a cero, C comenzará a fluctuar irregularmente, con una pequeña amplitud.
• Si 2 ν = ν _min - si la fuerza está en resonancia - entonces C oscilará suavemente, con una gran amplitud, en el área donde AB no es igual a cero, y continuará fluctuando incluso cuando AB vuelva a ser cero.

Fig. 1 muestra solo la situación resonante 2 ν = ν _min . Se puede ver que cuando la onda A pasa a través de la onda B, dejan una onda estacionaria C, que oscila con una frecuencia ν _min . Letra pequeña: en la fig. se muestra un boceto, no una solución exacta de las ecuaciones. La solución exacta tendrá muchas características pequeñas y complejas que eclipsan el significado físico básico, por lo que las eliminé para mayor claridad. Más adelante consideraremos una situación sin resonancia, que es mucho más complicada, pero también más importante para la física.

La aparición de una nueva partícula a partir de la aniquilación de los otros dos.

Les acabo de demostrar que los términos no lineales AB en la ecuación C pueden causar que la superposición de las ondas A y B produzca oscilaciones del campo C si la suma de las frecuencias de los campos A y B es igual a la frecuencia mínima del campo C. Pero qué pasaría si estas ondas tuvieran amplitud muy pequeña? ¿Qué puede suceder si un cuanto del campo A se encuentra con un cuanto del campo B?

• Si las frecuencias AB entran en resonancia con el campo C, entonces puede producirse un cuanto del campo C, es decir, una partícula real C, y los cuantos A y B desaparecerán - "aniquilarán".
• Además, los cuantos A y B pueden simplemente pasar uno al otro, sin crear la partícula C.
• Las leyes de la mecánica cuántica sugieren que la probabilidad de crear una partícula C es proporcional al cuadrado de y, que se multiplica por AB en la ecuación de movimiento C.
• Si las frecuencias no entran en la resonancia, la partícula real C no aparecerá. Sin embargo, puede producirse una perturbación temporal en el campo C, un ejemplo de lo que a menudo se llama la "partícula virtual" C, en cuyo caso los cuantos A y B pueden desaparecer. ¿Cuál es el resultado de tal perturbación? Describí parcialmente este proceso al final del artículo, en la sección "colas".

Este es el estado general de las cosas. Profundicemos en los detalles.

¿Qué significa para las partículas, es decir, cuantos de los campos A, B y C, estar en resonancia o no en resonancia? Vale la pena recordar que la energía de un cuanto está relacionada con su frecuencia debido a la ecuación E = h ν. Entonces traducimos nuestra discusión de ondas en una discusión de partículas.

Supongamos que nuestras ondas en los campos A y B consisten en cada uno de un cuanto. Estos cuantos no tienen masa, ya que A y B satisfacen las ecuaciones de la clase 0. Más precisamente, los términos lineales en sus ecuaciones de movimiento son los mismos que los de la clase 0. Como los cuantos A y B tienen la misma frecuencia, tienen la misma energía, E = h ν. Dado que el momento de un cuanto sin masa es p = E / c, los cuantos A y B tendrán momentos iguales en magnitud a h ν / c, pero en dirección opuesta, ya que uno de ellos se mueve hacia la izquierda y el otro hacia la derecha. Por lo tanto:

• La energía total de dos cuantos juntos será de 2hν.
• El impulso total de los dos cuantos juntos será cero.

Dado que la energía y el momento se conservan, la energía total después de la colisión de dos cuantos permanecerá igual a 2hν, y el momento total seguirá siendo cero.

En el caso de las ondas, vimos que, dado que la ecuación para C contiene un término de la forma AB, hay una resonancia cuando la frecuencia AB (que funciona como una fuerza oscilante) coincide con la frecuencia mínima C (que funciona como una bola en un resorte). Traducimos esta declaración a cuantos.

La frecuencia AB será 2 ν, por lo tanto, la energía del producto A y B, cuando las ondas A y B consisten en un cuanto, es igual a la suma de las energías A y B.

$$

$$E_ {AB} = 2 h \ nu = E_A + E_B$$

La frecuencia mínima C es igual a ν _min , lo que significa que para un cuanto estacionario del campo C, el momento es 0 y la energía

$$

$$E_C = h \ nu_ {min} = mc ^ 2$$

Donde m es la masa de la cantidad cuántica C.

Para resonancia, se requieren 2 ν = ν _min , es decir:

$$

$$E_A + E_B = 2 h \ nu = h \ nu_ {min} = mc ^ 2 = E_C$$

En resumen, la resonancia ocurre cuando las sumas de energías iguales de las partículas A y B (en cuyo caso los pulsos son iguales en magnitud y dirección opuesta) ¡son suficientes para crear una partícula estacionaria C! En el proceso, las partículas A y B son aniquiladas: su energía entra completamente en la creación de la partícula C. Esto se muestra (esquemáticamente) en la Fig. 2, que debes comparar con la fig. 1)


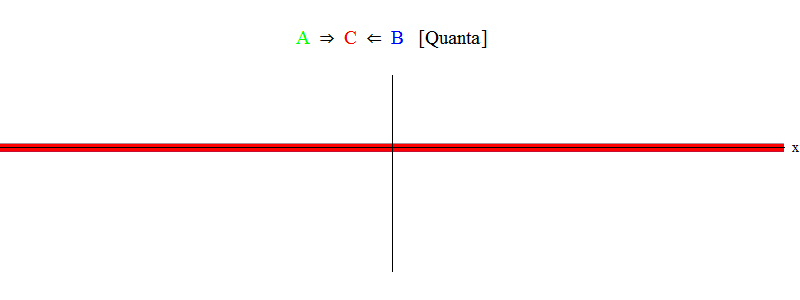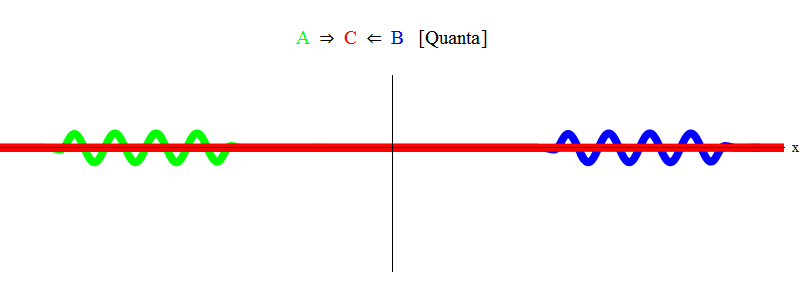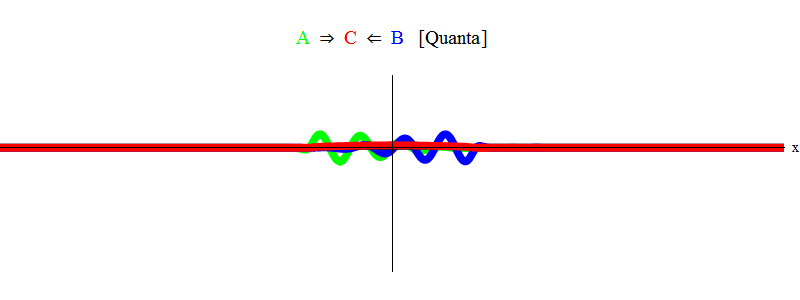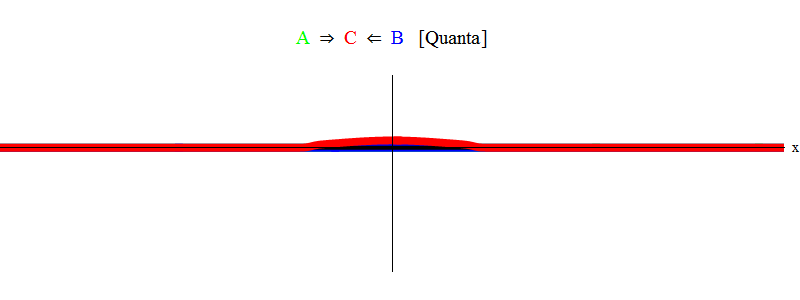Fig. 2

Razonamiento

Acabo de mostrarle el proceso A + B → C. En mi explicación, utilicé tres tipos diferentes de partículas para evitar confusiones. Pero la misma idea permite pasar por procesos de la forma A + A → C (por ejemplo, gluón + gluón → la partícula de Higgs, y básicamente así es como se obtiene la partícula de Higgs en el Gran Colisionador de Hadrones) y procesos de la forma A + A * → C, donde A * - antipartícula para A (por ejemplo, quark + antiquark → partícula Z, y así es como generalmente se obtienen las partículas Z en el LHC). Solo es necesario cambiar detalles menores, pero la esencia sigue siendo la misma.

Otro proceso que representa la misma idea, solo invertido en el tiempo: la descomposición de las partículas. La descomposición de una partícula de Higgs en dos fotones o partículas Z en un quark y un antiquark ocurre esencialmente como la animación en la Fig. 2, yendo en la dirección opuesta.

Colas

1. Si el término AB perturba el campo C sin resonancia, si 2 ν ≠ ν _min , ¿qué sucederá? Puede recordar que si empuja el columpio con el niño en la frecuencia incorrecta, o aplica una fuerza a la pelota en el resorte, oscilando con una frecuencia que no coincide con la frecuencia natural de las vibraciones, obtendrá una vibración desigual con una pequeña amplitud. En el contexto actual, sucede lo mismo con el campo C. El campo C se comportará de alguna manera, pero esto no conducirá a la aparición de un cuántico C. que se comporta bien. Simplemente se preocupa un poco. Esta mala indignación es un ejemplo de lo que se llama "Partículas virtuales C", pero esto no es una partícula (cuántica de una onda de campo C), a pesar de su nombre. Su masa es diferente de la masa de la partícula C; Puede ser más grande o más pequeño. A diferencia de la partícula C, no existe por sí sola durante mucho tiempo. Y no satisface las condiciones de amplitud que deben cumplir los cuantos reales. En cambio, a diferencia de la partícula C, que existe desde hace algún tiempo, con la fig. 2, existe una perturbación no resonante solo cuando A se cruza con B.

Pero esto no significa que no afecte nada. Por ejemplo, puede hacer que las partículas A y B reboten entre sí.

$$

$$A_ \ rightarrow + B_ \ leftarrow → C_ {ultraje} → A_ \ leftarrow + B_ \ rightarrow$$

En general, en un espacio tridimensional, un rebote o dispersión puede llevar al hecho de que A se mueve en cualquier dirección y B se mueve en la dirección opuesta. Ejemplos de tales procesos incluyen la dispersión de electrones y positrones debido a un fotón virtual, o la dispersión de quark y antiquark debido a un gluón virtual.

En presencia de otros campos, D y E, interactuando con C y participando en la ecuación de movimiento C

$$

$$d ^ 2C / dt ^ 2 - c ^ 2 d ^ 2C / dx ^ 2 = (2 \ pi \ nu_ {min}) ^ 2 C + y A B + y ’D E$$

Pueden ocurrir procesos mucho más interesantes:

A + B → C _{perturbación} → D + E

Así es: las partículas A y B pueden aniquilarse gracias a la partícula virtual C y dar lugar a la aparición de nuevas partículas D y E. ¡Esta es la segunda forma de crear nuevas partículas! Por ejemplo, un electrón puede colisionar con un positrón, aniquilarse a través de un fotón virtual (recuerde que esto significa "a través de una perturbación del campo de fotones a una frecuencia que no coincide con el resonante") y convertirse en un muón y un antimuón, o un quark y un antiquark. El quark inferior y el antiquark superior pueden colisionar, aniquilarse a través de una partícula W virtual y convertirse en un electrón y un antineutrino. O dos gluones pueden colisionar, aniquilarse a través de un gluón virtual y convertirse en un quark superior y un antiquark superior (esta es la forma más común de obtener quarks superiores en un LHC).

2. ¿Qué pasa si dos ondas en los campos A y B tienen frecuencias diferentes, ν _A y ν _B ? A frecuencias adecuadas, las partículas C todavía pueden aparecer, pero las condiciones de resonancia serán diferentes y la partícula C creada no será estacionaria. Vamos a resolverlo.

Si tienen frecuencias diferentes, entonces dos cuantos sin masa colisionando tendrán

• varias energías $$$E_A = h \ nu_A$ y $$$E_B = h \ nu_B$
• varios impulsos $$$p_A = + h \ nu_A / c$ y $$$p_B = - h \ nu_B / c$ (aquí, más significa a la derecha, menos a la izquierda).

El momento total p _A + p _B ahora no _es cero. Pero el impulso persiste. Por lo tanto, si la partícula C puede ocurrir como resultado de la aniquilación de las partículas A y B, tendrá un impulso p _C = p _A + p _B , por lo que se moverá hacia la izquierda o hacia la derecha, y no se detendrá. Si ν _A > ν _B , se moverá a la derecha, de lo contrario, a la izquierda.

¿Cuánta energía se requiere para crear una partícula móvil C? Para esto, se necesita más energía que para una estacionaria, como cualquier partícula masiva, su energía y momento deben satisfacer

$$

$$E_C ^ 2 = (p_Cc) ^ 2 + (mc ^ 2) ^ 2$$

Lo que significa que E _C = mc ² si p _C = 0, o más si el momento no es cero. La ley de conservación de la energía y el impulso nos dice que:

$$

$$E_C = E_A + E_B$$

$$

$$p_C = p_A + p_B = E_A / c - E_B / c$$

¿Dónde obtuve la última ecuación? Para una partícula sin masa, p = E / c, y para nuestras partículas en colisión A y B, sus momentos son opuestos, por lo que difieren en el signo. Sustituya esto en la ecuación anterior y obtenga:

$$

$$(E_A + E_B) ^ 2 = (E_A - E_B) ^ 2 + (mc ^ 2) ^ 2$$

Los términos E _A ² y E _B ² se aniquilan mutuamente, y al mover los términos E _A E _B a la izquierda, obtenemos:

$$

$$4 E_A E_B = (mc ^ 2) ^ 2$$

Dividiendo por h ² y usando la relación m = hν _min / c ² , obtenemos la condición de resonancia:

$$

$$(2 \ nu A) (2 \ nu B) = \ nu_ {min} ^ 2$$

Lo que se reduce correctamente cuando ν _A = ν _B a la ecuación para una partícula inmóvil C, 2 ν = ν _min . Si esta condición no se cumple, entonces la partícula C no se puede crear. Si está satisfecho, entonces es posible.

3. Observé que de la misma manera que la ecuación de movimiento para el campo C contiene el término AB, entonces la ecuación para B contiene el término AC. Recordemos estas ecuaciones:

$$

$$d ^ 2B / dt ^ 2 - c ^ 2 d ^ 2B / dx ^ 2 = y A C$$

$$

$$d ^ 2C / dt ^ 2 - c ^ 2 d ^ 2C / dx ^ 2 = (2 \ pi \ nu_ {min}) ^ 2 C + y A B$$

Entonces, si la superposición de las ondas A y B conduce a la aparición de una onda en el campo C, haciéndola distinta de cero, como en la Fig. 1, ¿debemos preocuparnos por el hecho de que esta nueva ola C se superpone con la onda A existente y conduce a un cambio en el campo B? Respondí que "sí, pero podemos descuidar esto". Podemos descuidar debido a una combinación de dos razones.

En primer lugar, debido al número "y" que aparece antes de las multiplicaciones de AB y BC. El impacto en el campo C del miembro AB es proporcional a y veces A multiplicado por B. El impacto en el campo B del miembro AC también es proporcional a y veces A multiplicado por C, pero esto a su vez será igual a y ² veces A multiplicado por por A multiplicado por B. Entonces, mientras y sea menor que 1, y ² será menor que y, por lo tanto, el efecto sobre B del miembro AC es pequeño comparado con el efecto sobre C del miembro AB, al menos para las ondas pequeñas A y B. las ondas son generalmente pequeñas: la partícula A es un cuanto de la onda en el campo A; por lo tanto, la onda A tiene pequeñas amplitudes d.

De lo cual se deriva la segunda razón, más extraña pero más convincente: vimos que si un cuanto A se encuentra con un cuanto B y se convierte en un cuántico C, entonces las ondas A y B desaparecen (aniquilan). Después de la creación de C, ya no hay ninguna onda A, por lo tanto, la CA es cero, es decir, no hay efecto en el campo B.

Y la última trampa: aunque no puedo probar esto sin cálculos adicionales, incluso si las ondas A y B consisten en un cuanto, como en la Fig. 2, luego el proceso en la Fig. 2 sería mucho más complicado si y fuera mucho mayor que 1. Por lo tanto, la simplicidad de la historia que conté requiere pequeños valores de y. En la naturaleza, la mayoría de los términos no lineales en física de partículas suelen ser pequeños, por lo que lo que dije se aplica a la mayoría de las situaciones aplicables en la práctica. Las excepciones son muy interesantes: conducen a la creación de objetos tan complejos como los protones y otros hadrones.