
La física es la ciencia compleja más compleja; es igual de compleja, tan fascinante. Si descartamos el componente matemático, la física se pone inmediatamente a disposición de cualquier persona con curiosidad e imaginación. Entenderemos fácilmente el concepto de la teoría de la gravedad, sin ecuaciones matemáticas complejas. Por lo tanto, para todos los que piensan en lo que hace que los arándanos sean azules y las fresas rojas; quien duda de que el sonido se propague en forma de ondas; cualquiera que se pregunte por qué el comportamiento de la luz es tan diferente de cualquier otro fenómeno en el universo, debe comprender que todo está relacionado con la física cuántica.
Este libro presenta (y desmitifica) para la gente común el mundo mágico de la ciencia cuántica, como ningún otro libro. Habla sobre conceptos científicos básicos, desde partículas de luz hasta estados de la materia y las causas del impacto negativo de los gases de efecto invernadero, revelando cada tema sin el uso de terminología científica específica, ejemplos de la vida cotidiana ordinaria. Por supuesto, un libro sobre física cuántica no puede prescindir de un conjunto mínimo de fórmulas y ecuaciones, pero este es un mínimo necesario, comprensible para la mayoría de los lectores. Según el autor, un libro que divulgue la ciencia debería ser accesible, pero no inferior al nivel del lector, sino para elevar y desarrollar su intelecto y su nivel cultural general.
Raquetbol Cuántico y Color Fruta
Una propiedad clave de los electrones unidos a los átomos y las moléculas es que sus estados de energía son discretos. Decimos que la energía de un electrón puede cuantificarse, es decir, un electrón unido a un átomo o molécula puede tener solo algunos valores de energía específicos. La energía cambia paso a paso, y estos pasos tienen ciertos tamaños discretos. Los estados energéticos son como las escaleras. Puedes pararte en un escalón o subir al siguiente escalón más alto. Sin embargo, es imposible estar a medio camino entre los dos pasos. Estos valores de energía discretos o cuantificados a menudo se denominan niveles de energía. A diferencia de las escaleras comunes, los intervalos entre los niveles de energía generalmente no son los mismos.
Un área importante de la investigación cuántica moderna es el cálculo de los estados electrónicos de las moléculas. Esta área se llama química cuántica. Dichos cálculos permiten obtener niveles de energía cuantificados para electrones en moléculas (niveles de energía), así como calcular la estructura de las moléculas. El cálculo de la estructura de la molécula da la distancia entre los átomos y las posiciones de todos los átomos en la molécula con una precisión limitada solo por el principio de incertidumbre. Por lo tanto, los cálculos de la mecánica cuántica permiten determinar el tamaño y la forma de las moléculas. Dichos cálculos son importantes para comprender los principios fundamentales de la unión de los átomos a las moléculas y para la construcción de nuevas moléculas. Con el desarrollo de la teoría cuántica y la aparición de computadoras cada vez más potentes y complejas capaces de resolver problemas matemáticos laboriosos, se pueden estudiar moléculas cada vez más grandes utilizando los métodos de la química cuántica. Una de las aplicaciones más importantes de la teoría cuántica es el desarrollo de productos farmacéuticos. Las moléculas pueden diseñarse de modo que tengan el tamaño deseado y se "ajusten" en forma a loci específicos de proteínas o enzimas.
La química cuántica requiere cálculos muy laboriosos. Incluso para el átomo de hidrógeno más simple, los cálculos de mecánica cuántica son matemáticamente muy complicados. Un átomo de hidrógeno consiste en un electrón unido a un protón. Un protón, que es el núcleo de un átomo de hidrógeno, es una partícula cargada positivamente y un electrón está cargado negativamente. La atracción de un electrón cargado negativamente a un protón cargado positivamente los mantiene unidos, manteniendo unido el átomo de hidrógeno. Los detalles del cálculo de los niveles de energía del átomo de hidrógeno no se presentarán aquí, pero en los siguientes capítulos consideraremos algunas características de los resultados de estos cálculos. Dan los niveles de energía del átomo de hidrógeno y sus funciones de onda. Son las funciones de onda, es decir, las ondas de amplitud de probabilidad para un átomo de hidrógeno, que son el punto de partida para comprender todos los átomos y moléculas. Los átomos y las moléculas son complejos porque son sistemas tridimensionales absolutamente pequeños, y es necesario tener en cuenta cómo los protones y los electrones interactúan entre sí.
Una partícula en una caja: un caso clásico
Hay una tarea muy simple relacionada con nuestro tema. Se conoce como el problema de partículas en una caja. No requiere una matemática complicada para resolverlo, pero esta solución nos permite ilustrar propiedades importantes de los electrones unidos, por ejemplo, la cuantificación de los niveles de energía y la naturaleza ondulatoria de los electrones en estados unidos. Antes de analizar la naturaleza del electrón en una caja unidimensional de tamaños atómicos, discutimos el problema clásico de un campo de juego unidimensional ideal para el racquetball para identificar las diferencias entre los sistemas clásico (grande) y cuántico-mecánico (absolutamente pequeño).
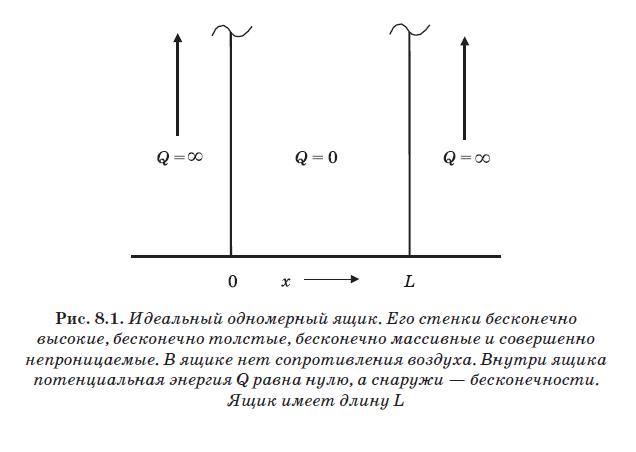
En la fig. 8.1 representa la "caja" perfecta. El es unidimensional. Sus paredes se consideran infinitamente altas, infinitamente masivas y completamente impenetrables. No hay aire dentro de la caja para resistir el movimiento. En la figura, el interior de la caja se designa Q = 0, y el exterior - Q = ∞. Anteriormente se dijo que una partícula se llama libre y que ninguna fuerza actúa sobre ella. Las fuerzas surgen cuando una partícula interactúa con algo. Por ejemplo, una partícula cargada negativamente, como un electrón, puede interactuar con un protón cargado positivamente. La interacción en forma de atracción entre partículas con carga opuesta generará una fuerza que actúa sobre el electrón. Cuando se controlan electrones en un CRT (ver Fig. 7.3), un campo eléctrico genera una fuerza que actúa sobre los electrones y los obliga a cambiar de dirección.
Una medida de la interacción de una partícula con algo que la afecta, como un campo eléctrico, se llama potencial y tiene la dimensión de energía. En el futuro, el potencial se denotará con la letra Q. Dentro de la caja, Q = 0, como en el caso de una partícula libre. Esto significa que la partícula no interactúa con nada dentro de la caja. No hay campos eléctricos ni resistencia al aire. Sin embargo, fuera de la caja, Q = ∞. Potencial infinito significa que una partícula tendría que tener energía infinita para estar en áreas fuera de la caja. La expresión Q = ∞ es solo una forma de formalizar la afirmación de que las paredes de la caja son ideales. Una partícula no puede penetrar a través de las paredes ni saltar sobre ellas, sin importar cuán grande sea su energía. Si coloca una partícula en dicha caja, no puede escaparse y siempre permanecerá dentro de ella. En este sentido, la partícula está encerrada en una caja. Puede estar en una región de espacio de longitud L, pero en ningún otro lugar.
En la fig. La Figura 8.2 muestra una pelota para jugar racquetball, rebotando en las paredes de una cancha de racquetball clásica (grande) ideal de una dimensión. Como ya se mencionó, estas paredes son ideales, pero no hay resistencia al aire en el interior. Además, la pelota también es ideal, es decir, tiene una elasticidad absoluta. Cuando la pelota choca con la pared, se contrae como un resorte y se endereza nuevamente, haciendo que rebote. Las bolas reales no son perfectamente elásticas. Cuando la bola se comprime al impactar, no toda la energía gastada en la compresión se repele desde la pared. Parte de la energía gastada en comprimir la pelota se calienta. Sin embargo, aquí consideraremos la pelota perfectamente elástica. Al golpear una pared, toda la energía cinética de la pelota, que hace que se comprima, se gasta en empujar la pelota lejos de la pared. Por lo tanto, la velocidad de la pelota justo antes de la colisión con la pared es igual a la velocidad de su rebote después de la colisión.
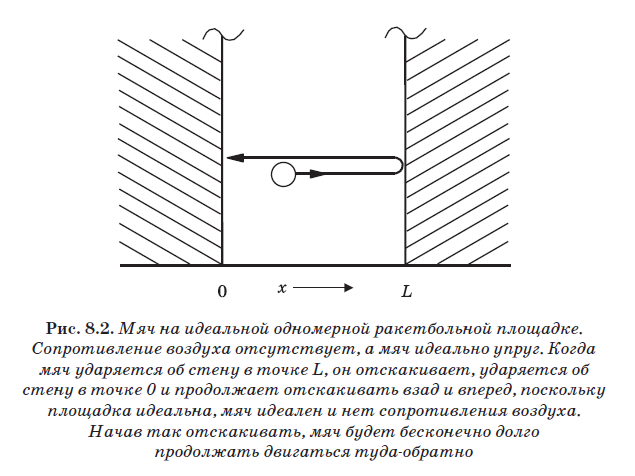
En este terreno de racquetball ideal, la pelota rebota en las paredes sin ninguna pérdida de energía; Además, no hay resistencia al aire ni gravedad. Por lo tanto, la pelota siempre se moverá hacia adelante y hacia atrás, reflejándose en las paredes. Golpea la pared en el punto L, rebota, choca con la pared en el punto 0, rebota nuevamente y continúa moviéndose hacia adelante y hacia atrás. Dentro de la caja, dado que el potencial es cero (ver Fig. 8.1), no hay fuerzas que actúen sobre la pelota. Por lo tanto, su energía es puramente cinética:
donde m es la masa de la pelota y V es su velocidad. Si la pelota experimenta influencias externas débiles, su velocidad será ligeramente más baja y el valor Ek también disminuirá ligeramente. En este racquetball ideal, la energía puede cambiar continuamente. El valor de Ek puede aumentar o disminuir arbitrariamente dependiendo solo de la fuerza del impacto en la pelota.
Otra característica importante del racquetball clásico es la capacidad de detener la pelota para que quede inmóvil en el piso. En esta situación, su velocidad es cero: V = 0. Y como V = 0, entonces Ek = 0. En V = 0, el momento también es cero, ya que p = mV, por lo que sabemos el momento exactamente. Si la pelota yace en el piso (V = 0), entonces se conoce su posición. Si denotamos esta posición x (ver Fig. 8.2), entonces el valor de x estará en el rango de 0 a L. El valor de x no puede tomar ningún otro valor, ya que la pelota está en la cancha (en el cuadro) y no puede estar fuera de Para paredes perfectas. La pelota se puede colocar en una posición específica x en el piso de la cancha, y luego su posición se conocerá con seguridad. Esta es una propiedad de un patio de juegos macroscópico, incluso ideal. Este es un sistema clásico, y en él se puede conocer de forma precisa y simultánea el momento p y la posición x.
La cancha de racquetball tiene una longitud de 12 m, el diámetro de la pelota es de 5.6 cm y su peso es de aproximadamente 0.04 kg. Obviamente, el juego de racquetball es descrito por la mecánica clásica. Con la ayuda de la luz, puede seguir el rebote de la pelota de un lado a otro sin afectarlos.
Partícula en una caja - Caso cuántico
¿Qué cambiará si ahora pasamos a la consideración del racquetball cuántico? El sitio sigue siendo ideal, pero ahora su longitud no es de 12 m, sino de 1 nm (10–9 m). Además, la partícula tiene una masa de electrones de 9.1 10–31 kg, y no 0.04 kg. Por lo tanto, este es el problema de una partícula cuántica en una caja.
Podemos decir de inmediato que la energía más pequeña de una partícula cuántica en una caja de tamaño nanométrico no puede ser cero. En un campo de racquetball clásico, la velocidad de la pelota V es posible, que es igual a cero, lo que significa que el impulso p = mV puede ser cero. Además, la posición de la pelota x tiene un significado claramente definido. Por ejemplo, la pelota puede permanecer quieta (V = 0) exactamente en el medio de la cancha, lo que corresponde a x = L / 2. En este caso, para nuestro racquetball clásico, ∆p = 0 y ∆x = 0. El valor del producto ∆x∆p = 0 no corresponde al principio de incertidumbre de Heisenberg, que es normal, ya que estamos hablando del sistema clásico. Sin embargo, una partícula absolutamente pequeña en una caja de tamaño nanométrico es un objeto cuántico y debe obedecer el principio de incertidumbre, que establece que ∆x∆p ≥ h / 4. Si V = 0 yx = L / 2, entonces conocemos tanto x como p, lo que significa que ∆x∆p = 0, como en el racquetball clásico. Para un sistema cuántico, esto no es posible. Por lo tanto, V no puede ser igual a cero. Una partícula no puede permanecer inmóvil en un punto dado. Y si el valor de V no es cero, entonces el valor de Ek no puede ser igual a cero. El principio de incertidumbre dice que la energía más pequeña de nuestro racquetball cuántico no puede ser cero. Una bola cuántica nunca permanece inmóvil.
Valores de energía de partículas cuánticas en una caja
¿Qué energía puede tener una partícula cuántica en una caja de tamaño nanométrico? Esta pregunta puede responderse sin cálculos complicados, pero primero debemos volver a las olas nuevamente. En el capítulo 6 hablamos sobre las funciones de onda de las partículas libres. La función de onda de una partícula libre con un momento específico p es una onda que se extiende por todo el espacio. Por lo tanto, un electrón con un momento perfectamente definido es una onda deslocalizada, que cubre todo el espacio. La probabilidad de detectar un electrón libre es la misma en todas partes. Tal electrón tiene una energía cinética bien definida Ek = 1 / 2mV2, ya que tiene un momento bien definido p = mV.
El electrón en la caja nanométrica es similar a nuestra partícula libre con respecto a la región interna de la caja, donde Q = 0. No hay potencial dentro de la caja, y por lo tanto no hay fuerzas que actúen sobre la partícula. A este respecto, es muy similar a una partícula libre, en la que tampoco actúan fuerzas. Sin embargo, hay una diferencia importante entre la partícula en la caja y la partícula libre: estas son las paredes de la caja. El electrón en la caja está solo dentro de la caja. La naturaleza ideal de la caja no permite que su función de onda se extienda a todo el espacio. La partícula está dentro de la caja y nunca puede estar afuera. La función de onda establece la amplitud de la probabilidad de detectar una partícula en una determinada región del espacio. Esta es una interpretación nativa de la función de onda. Si nuestro electrón puede ser detectado solo dentro de la caja y nunca afuera, entonces la probabilidad de su detección en la caja debe ser finita y fuera de cero. Si la probabilidad de encontrar una partícula fuera del cuadro es cero, entonces la función de onda debe ser cero en todos los puntos fuera del cuadro.
Entonces, llegamos a la conclusión de que la función de onda de una partícula en una caja es similar a la función de onda de una partícula libre, pero la función de onda debe ser cero fuera de la caja. En su interpretación de la naturaleza de la función de onda mecánica cuántica, Born impuso algunas restricciones físicas sobre la forma que puede tomar la función de onda. Una de ellas es que una buena función de onda debe ser continua. Esta condición significa que la función de onda debe cambiar suavemente de un lugar a otro. Un cambio de posición infinitamente pequeño no puede conducir a un salto inesperado en la probabilidad. Este es un pensamiento muy simple. Si la probabilidad de detectar una partícula en una región muy pequeña del espacio es, por ejemplo, del 1%, entonces un desplazamiento de una cantidad inimaginablemente pequeña no puede hacer que la probabilidad de detectar una partícula sea igual al 50%. Esto queda claro a partir de las imágenes de paquetes de ondas en la Fig. 6.7. La probabilidad varía suavemente de un lugar a otro. Esto nos permite agregar algo a la descripción de las funciones de onda de una partícula en una caja, además del hecho de que son ondas con amplitudes finitas dentro de la caja y amplitud cero afuera. Dado que la función de onda debe ser continua, debe tener una amplitud cero directamente en la pared de la caja desde el interior para que coincida con la amplitud cero de la función de onda fuera de la caja.
En la fig. 8.3 muestra la discontinuidad (prohibida) de la función de onda dentro de la caja. Se indica la función de onda (letra griega "fi"). El eje vertical representa la amplitud de la función de onda. La línea discontinua indica su nivel cero. Las funciones de onda, que son ondas de amplitud de probabilidad, pueden fluctuar entre valores positivos y negativos. La función de onda que se muestra en la Fig. 8.3, tiene valores cercanos a las paredes distintos de 0. Sin embargo, la función de onda debe ser cero fuera del cuadro, es decir, para valores de x menores que 0 y mayores que L, debe ser cero. En la figura, la función de onda salta inesperadamente de un valor distinto de cero cerca de la pared dentro de la caja a un valor cero inmediatamente detrás de la pared fuera de la caja. Por lo tanto, la función de onda que se muestra en la Fig. 8.3 no es válido porque no es continuo. Esta función no puede representar una partícula cuántica en una caja.
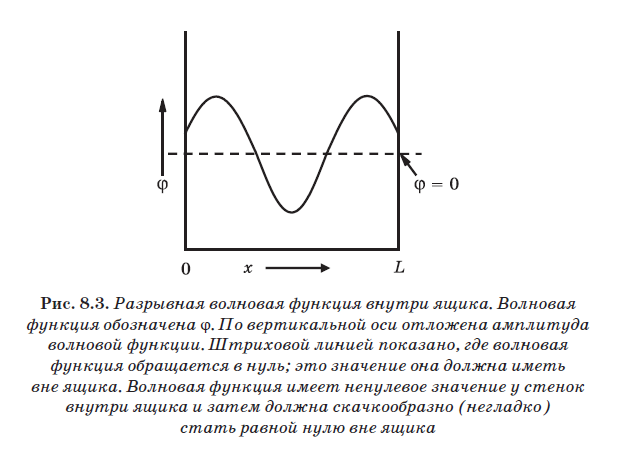
La función de onda debe tener un valor cero en las paredes.
Para que las funciones de onda que representan la partícula en la caja sean físicamente aceptables, sus valores en las paredes deben ser cero, y entonces no experimentarán una brecha en las paredes. No es difícil cumplir esta condición. La función de onda fluctúa entre valores positivos y negativos. Cada vez, pasando de valores positivos a negativos o de negativo a positivo, pasa por cero. De hecho, los puntos cero están separados entre sí por la mitad de la longitud de onda. Por lo tanto, para obtener buenas funciones de onda de una partícula en una caja, debemos elegir ondas cuya longitud les permita apilarse en la caja para que los puntos cero se ubiquen exactamente en las paredes.
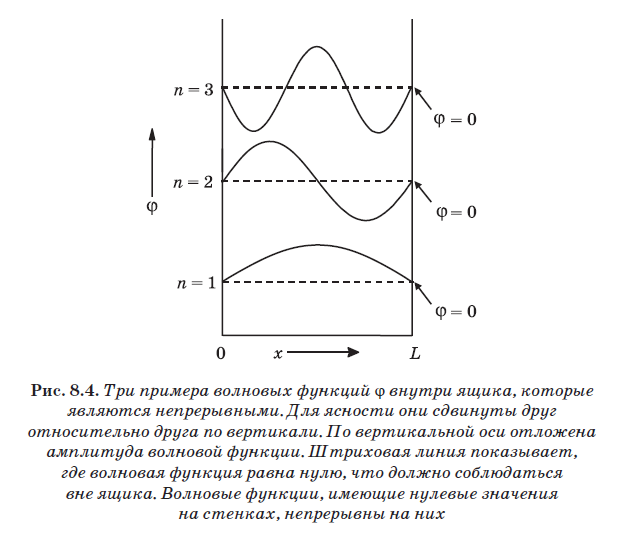
En la fig. 8.4 muestra tres ejemplos de ondas que son adecuadas para el papel de las funciones de onda para una partícula en una caja. El más bajo de ellos se designa n = 1 y consiste en una media onda. Comienza a la izquierda en la amplitud 0, pasa el máximo y luego cae nuevamente a cero en la pared en el punto L. La siguiente onda, ubicada arriba y marcada n = 2, consiste en una oscilación completa. También comienza en la pared izquierda en la amplitud 0, pasa un pico positivo, vuelve a cero, luego sigue un pico negativo y vuelve a cero en la pared en el punto L. La onda indicada por n = 3 contiene un período medio. Es adecuada cualquier onda que contenga un número entero de medias ondas, es decir, 1, 2, 3, 4, 5, y así sucesivamente, la mitad de la longitud de onda, y ubicada de modo que comience en cero a la izquierda y termine en cero a la derecha.
El valor n es el número de medias ondas de una función de onda particular. Para n = 1, la longitud de onda es 2L, ya que la longitud de la caja es L, yn = 1 corresponde a la mitad de la longitud de onda. Para n = 2, la longitud de onda es L, ya que se coloca exactamente una longitud de onda entre las paredes. Para n = 3, se colocan tres medias ondas entre las paredes, es decir, 1.5 = L. En este caso = L / 1.5, es decir = 2L / 3. Tenga en cuenta que aquí se encuentra una regla general: = 2L / n, donde n es un número entero. Para n = 1 obtenemos = 2L, para n = 2 - = 2L / 2, para n = 3 - = 2L / 3, etc.
»Se puede encontrar más información sobre el libro en
el sitio web del editor»
Contenidos»
ExtractoPara los lectores de este blog, un descuento del 20% en el cupón -
Fire