Cómo funciona el campo de Higgs: 2) por qué el campo de Higgs en promedio no es cero

Cómo funciona el campo de Higgs:

1. Idea principal
2. ¿Por qué se promedia el campo de Higgs distinto de cero?
3. ¿Cómo aparece la partícula de Higgs?
4. ¿Por qué es necesario el campo de Higgs?

¿Cómo es que el campo de Higgs en la naturaleza no tiene un valor promedio de cero, mientras que otros campos de la naturaleza (aparentemente elementales) que conocemos tienen cero? [Letra muy pequeña: otros campos, con la excepción del campo gravitacional del nivel más bajo, se denominan métricos, esto le permite determinar la existencia de espacio y tiempo].

Primero, los campos de fermiones no pueden tener un gran valor constante distinto de cero en la naturaleza. Esto se debe a la diferencia entre fermiones y bosones. Los bosones pueden ser, en promedio, distintos de cero, pero los fermiones no. Entonces puedes olvidarte de los electrones (y sus primos muones y tau), de los neutrinos y los quarks. Letra pequeña: los fermiones pueden emparejarse entre sí o con antifermiones y formar bosones compuestos, que en promedio pueden ser distintos de cero. Esto es así para los quarks superiores e inferiores y sus antiquarks, y para los electrones en un superconductor. Pero esta es una larga historia, y no concierne a la nuestra directamente.

¿Qué pasa con los campos de fotones, gluones, W y Z? Todos estos son bosones. En principio, estos campos podrían tener un valor promedio constante distinto de cero sobre el Universo. Pero los experimentos, no la teoría, dicen que este no es el caso. Un valor no cero suficientemente grande del campo eléctrico conduciría a la aparición de varios efectos, que no observamos. El más importante de estos sería una violación de la invariancia rotacional a gran escala. Un campo eléctrico es un vector (spin-1), indica en cierta dirección, por lo tanto, si no es cero, entonces la dirección en la que este valor indica debería ser diferente de todos los demás. (Fig. 1, abajo a la izquierda).


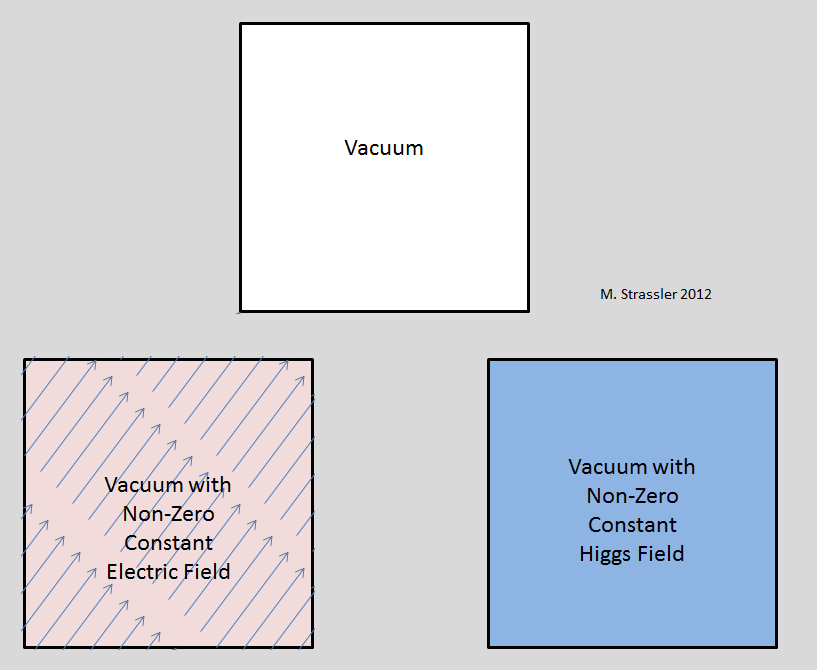Fig. 1

El campo de Higgs es escalar (spin-0), no indica en ninguna parte. Entre otros campos escalares (ni elementales ni relativistas), podemos dar ejemplos del campo de densidad del aire, el campo de presión dentro de la Tierra y la temperatura del océano. En cada punto del espacio y el tiempo, la densidad, la presión o la temperatura son solo un número, y el campo eléctrico es un número y una dirección. Entonces, si el campo de Higgs tiene un valor distinto de cero, no surge ninguna dirección preferida - Fig. 1, abajo a la derecha. Lo que es más extraño (ya que es relativista), el campo de Higgs no genera ningún marco de referencia preferido. Para la densidad del aire, existe un sistema de referencia preferido, ya que descansa en relación con el aire o se mueve a través de él. Pero para el campo de Higgs esto no es así; Todos los observadores descansan en relación con él. Por lo tanto, el éxito del SRT de Einstein, que describe todo tipo de fenómenos, no contradice la presencia de un campo escalar relativista de valor distinto de cero, como el campo de Higgs. Brevemente, en presencia de un campo de Higgs distinto de cero, el vacío se comporta exactamente como se comportaría en H = 0; su presencia solo puede detectarse mediante el efecto sobre la masa de partículas (o mediante algo más dramático, por ejemplo, el uso de LHC para crear partículas de Higgs).

La forma más simple para el campo de Higgs sería mantener un valor distinto de cero en todo el Universo si tuviera un valor de equilibrio distinto de cero H ₀ involucrado en su ecuación de movimiento de clase 1:

$$

$$d ^ 2H / dt ^ 2 - c ^ 2 d ^ 2H / dx ^ 2 = - (2 \ pi \ nu_ {min}) ^ 2 (H - H_0)$$

(Debe ser de clase 1, no de clase 0, por razones que nos serán claras después de discutir la partícula de Higgs). De hecho, la situación es un poco más complicada. La ecuación correcta se vería así:

$$

$$d ^ 2H / dt ^ 2 - c ^ 2 d ^ 2H / dx ^ 2 = a ^ 2 H - b ^ 2 H ^ 3$$

Donde ayb son constantes (¡sus cuadrados son positivos! Observe el signo más delante de un ² H, y compárelo con el menos en la ecuación anterior), sobre lo que aprenderemos más adelante. Esto puede reescribirse como:

$$

$$d ^ 2H / dt ^ 2 - c ^ 2 d ^ 2H / dx ^ 2 = - b ^ 2 H (H ^ 2 - [a / b] ^ 2)$$

Si H (x, t) es una constante en el espacio y el tiempo, entonces dH / dt = dH / dx = 0, por lo tanto

$$

$$0 = - b2 H (H2 - [a / b] ^ 2)$$

(cuando H (x, t) es una constante en x y t), y tiene soluciones (por ahora, simplificaremos mucho todo):

1. H = 0
2. H = + a / b
3. H = - a / b

En otras palabras, las posiciones de equilibrio son tres, no una. Letra pequeña: aquí lo simplifico enormemente, pero sin perjuicio del significado.

Esto no está claro de inmediato, pero la solución H = 0 es inestable. La situación es similar a la ecuación de movimiento de una pelota en un tazón de la forma que se muestra en la Fig. 2 - similar al fondo de una botella de vino. También tiene tres posiciones de equilibrio, una en 0 y dos en ± x ₀ . Pero, obviamente, la posición en 0 es inestable: cualquier empuje hará que la bola roja ruede lejos de x = 0, un cambio cardinal en la situación. Por el contrario, el equilibrio en x = x _{0 es} estable, ya que cualquier empuje hará que la bola verde oscile con una pequeña amplitud alrededor del punto x = x ₀ , no un cambio tan drástico. Lo mismo será cierto para una bola verde claro en x = -x ₀ . Del mismo modo, aunque H = 0 será la solución a la ecuación para el campo de Higgs, la historia de nuestro Universo resultó ser lo suficientemente complicada como para garantizar que el campo de Higgs debería ser pateado adecuadamente, por lo que no podría permanecer en esa posición. En cambio, el campo de Higgs estaba en una solución con un valor distinto de cero y en una situación estable.



Durante décadas, gracias a una combinación de experimentos y teoría, supimos que el valor del campo de Higgs (que tradicionalmente se llama "v") es 246 GeV. Esto nos da una idea de esas constantes a y b:

a = vb = (246 GeV) b

Por lo tanto, podemos determinar a a través de b, y podemos reescribir la ecuación de movimiento de Higgs:

$$

$$d ^ 2H / dt ^ 2 - c ^ 2 d ^ 2H / dx ^ 2 = - b ^ 2 H (H ^ 2 - v ^ 2)$$

Pero esto no nos da una idea de b en sí. En el próximo artículo aprenderemos más sobre él.

Ahora, aunque he preparado todo para que H pueda ser igual a v o –v, no importa si el campo de Higgs es positivo o negativo (de hecho, hay aún más posibilidades, ver más abajo); el mundo resultará exactamente igual, con la misma física, ya que nada depende del signo de H. No se hace evidente de inmediato, pero lo es; una pista: donde sea que encuentre H en las ecuaciones que estoy describiendo o en la descripción de cómo funciona el campo de Higgs, H ² aparece en todas partes, y no solo H, y H ² no depende de H = v o H = -v . [Letra pequeña: de hecho, H es un campo complejo, con las partes real e imaginaria, por lo que H puede ser igual a v multiplicado por cualquier número complejo z para el cual | z | = 1; y de hecho, H * H = | H | ² , pero no depende de z. ¡E incluso eso no es todo! Pero suficiente por hoy.]

Si encuentra una manera (por ejemplo, colisionando protones entre sí en el Gran Colisionador de Hadrones) de alguna manera empujar o introducir perturbaciones en el campo de Higgs, oscilará de un lado a otro, es decir, aparecerán ondas en él en la forma

$$

$$H = v + A cos [2 \ pi (\ nu t - x / \ lambda)]$$

Donde A es la amplitud de onda, ν y λ son la frecuencia y la longitud de onda, y la relación entre ν y λ depende de la forma exacta de la ecuación de movimiento, en particular, de b y v. Dado que el campo de Higgs es cuántico, la amplitud de estas ondas se cuantificará, y el cuanto de estas ondas es lo que llamamos la partícula de Higgs. La próxima vez consideraremos las propiedades de estas partículas.