Cómo funciona el campo de Higgs: 3) cómo aparece la partícula de Higgs

Cómo funciona el campo de Higgs:

1. Idea principal
2. ¿Por qué se promedia el campo de Higgs distinto de cero?
3. ¿Cómo aparece la partícula de Higgs?
4. ¿Por qué es necesario el campo de Higgs?

En un artículo anterior, describí cómo y por qué el campo de Higgs no tiene un valor medio de cero. Ahora quiero describir qué es una partícula de Higgs y cómo surge su masa de las ecuaciones.

Quiero recordarle que si no se menciona lo contrario, siempre describo la forma más simple posible del campo y la partícula de Higgs, la llamada Modelo estándar de Higgs. También son posibles formas más complejas; por ejemplo, pueden existir varios campos de Higgs simultáneamente, en lugar de uno. Quizás describa un caso más complejo en uno de los siguientes artículos.


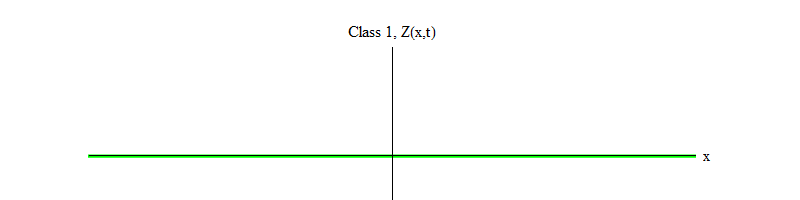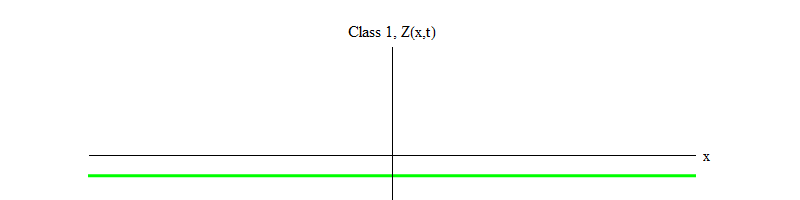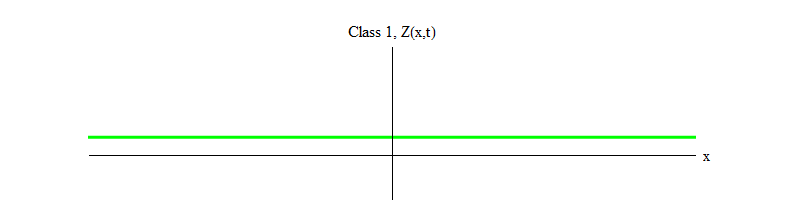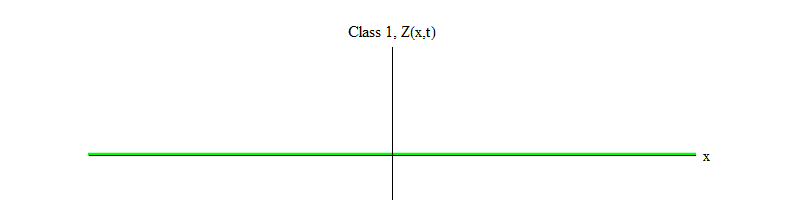Fig. 1: un campo de clase 1 fluctúa en el tiempo alrededor de un valor estable Z (x, t) = 0

En el último artículo, no enfaticé este hecho, pero entre los campos elementales que descubrimos en la naturaleza, el campo de Higgs es único. Todos los campos, excepto Higgs, satisfacen las ecuaciones de movimiento de la clase 0 o 1. En realidad (aunque probablemente este no sea el caso para todos los campos en la naturaleza), todos los campos que sabemos que satisfacen las ecuaciones de la clase 1 hacen esto porque el campo de Higgs no es cero . Si fuera cero, todos satisfarían las ecuaciones de la clase 0 (como expliqué en el primer artículo). En cambio, el campo de Higgs satisface una ecuación que se puede llamar una ecuación de clase -1.

Para el campo Z (x, t), las clases que definí se ven así:

$$

$$d ^ 2Z / dt ^ 2 - c ^ 2 d ^ 2Z / dx ^ 2 = - B ^ 2 Z \ quad [Clase 1 - masivo \; partículas] \\ d ^ 2Z / dt ^ 2 - c ^ 2 d ^ 2Z / dx ^ 2 = 0 \ quad [Clase 0 - sin masa \; partículas] \\ d ^ 2Z / dt ^ 2 - c ^ 2 d ^ 2Z / dx ^ 2 = + B ^ 2 Z \ quad [Clase -1 - inestable]$$

Las ecuaciones implican que B ² > 0.


Fig. 2: Un campo de clase -1 deja el equilibrio inestable Z (x, t) = 0.

El signo menos entre la clase 1 y la clase -1 es muy importante. En ambos casos, las soluciones de las ecuaciones contienen Z (x, t) = 0 como uno de los casos especiales, pero para la clase 1 Z (x, t) = 0 es estable, es decir, Z (x, t) puede fluctuar alrededor de cero; Estas son ondas de comportamiento decente con un cuanto cuántico. Y viceversa, la clase -1 Z (x, t) = 0 es inestable, es decir, Z (x, t) no fluctuará, sino que crecerá a más y más valores. Si no cambia la ecuación, la magnitud del campo volará hasta el infinito. Más precisamente, si la solución a la ecuación de la clase 1 es la oscilación Z, como en la Fig. 1, la solución a una ecuación de clase -1 es un crecimiento exponencial de Z, como en la Fig. 2)

Para el campo de Higgs, así como para cualquier campo existente en la naturaleza, la ecuación de la clase -1 se cambia utilizando términos que limitan el crecimiento exponencial y evitan que el campo llegue al infinito. Como vimos en el artículo anterior, el campo de Higgs obedece a la ecuación de movimiento

$$

$$d ^ 2H / dt ^ 2 - c ^ 2 d ^ 2H / dx ^ 2 = - b ^ 2 H (H ^ 2 - v ^ 2) = + (bv) ^ 2 H - b ^ 2 H ^ 3$$

Pertenece a la clase -1 cuando H es casi cero, pero tiene un miembro importante de H ³ . Aquí b es un número positivo, y v es la posición de equilibrio para H. Esta ecuación asegura que si el campo H comienza en el punto H = 0 y se mueve desde la posición de equilibrio inestable a H positivo, entonces oscilará alrededor de la posición de equilibrio estable en H = v (fig. 3).


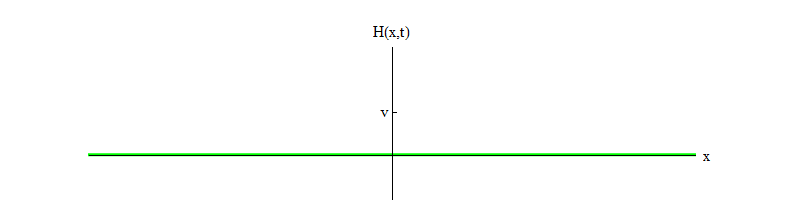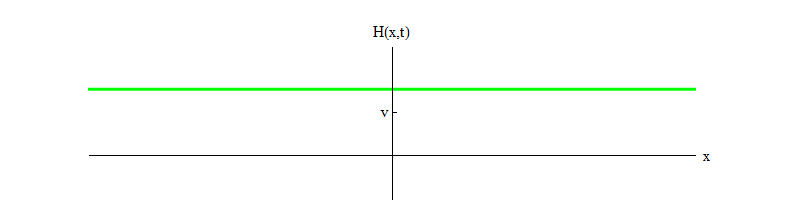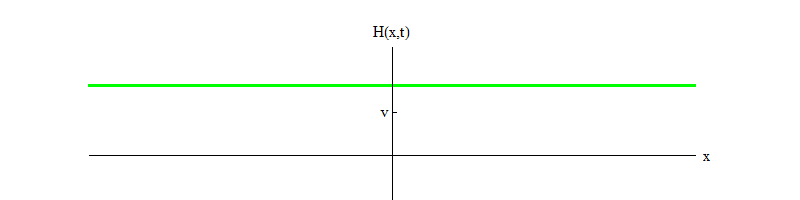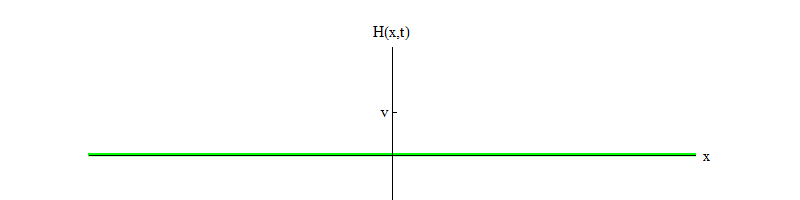Fig. 3

Con el tiempo, las oscilaciones se desvanecerán, debido a los términos de la ecuación de movimiento, que omití por brevedad; Permiten que parte de la energía de las oscilaciones del campo H se transfiera a ondas de otros campos (estos son los mismos términos no lineales que permiten la descomposición de las partículas de Higgs ). Con el tiempo (Fig. 4), el campo H se calmará en la posición H = v.


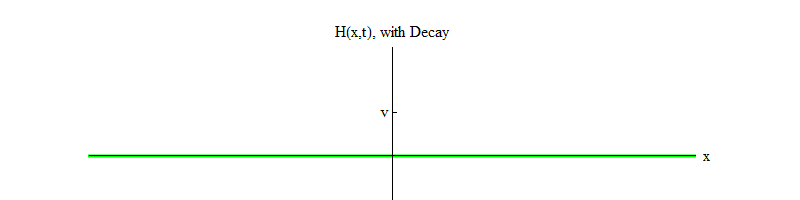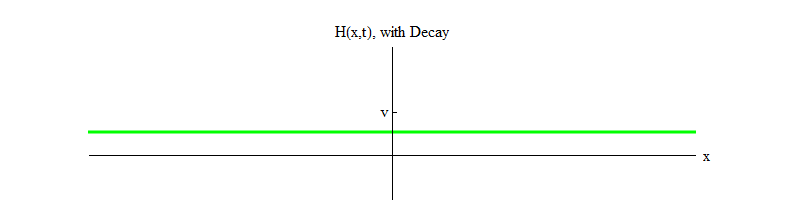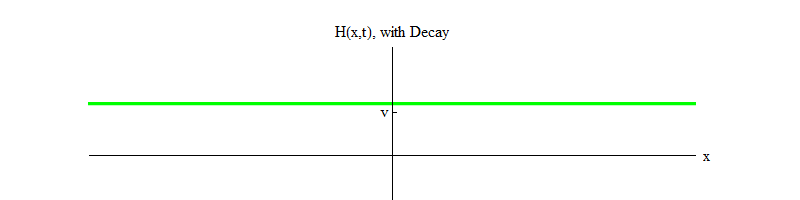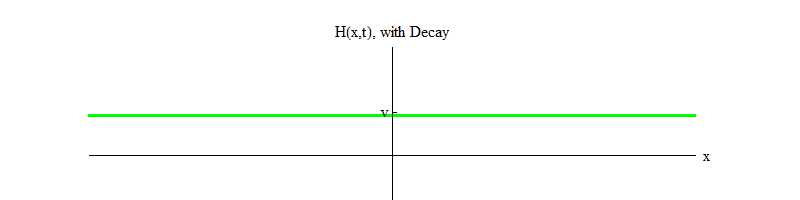Fig. 4 4

Si algún proceso físico golpea el campo desde la posición H = v en una pequeña región del espacio, el campo emitirá ondas de la forma

$$

$$H = v + A cos [2 \ pi (\ nu t - x / \ lambda)]$$

Donde A es la amplitud de onda, ν y λ es su frecuencia y longitud de onda, y la relación entre ν y λ depende de la forma exacta de la ecuación de movimiento, en particular, de b y v. Y los cuantos de estas ondas serán las partículas de Higgs. Pregunta por millón: ¿cuál es la masa de la partícula de Higgs? Para calcular esto, necesitamos, como siempre se requiere para las partículas (que representan cuantos de onda en campos relativistas), determinar la relación entre la frecuencia ν y la longitud de onda λ de las ondas del campo correspondiente, y luego multiplicar el resultado por la constante de Planck h para obtener la relación entre la energía y el momento cuántico de estas ondas, que nos dirá la masa del cuanto (es decir, partículas).

Hacemos exactamente eso con el campo S (x, t) mencionado en el primer artículo . Escribimos una versión desplazada del campo de Higgs, expresándola como H (x, t) = v + h (x, t) , y la sustituimos en la ecuación de movimiento del campo H. h (x, t) Escribiré en negrita para distinguirlo de la constante de Planck h. En el ejemplo para el campo S dado en el artículo de revisión, se indica una ecuación de movimiento simple, por lo que el cambio no cambió la masa de la partícula S. ¡Pero en este caso no lo es! La ecuación de movimiento del campo de Higgs es más compleja, por lo que la ecuación para h es muy diferente de la ecuación original para H:

$$

$$d ^ 2 \ textbf {h} / dt ^ 2 - c ^ 2 d ^ 2 \ textbf {h} / dx ^ 2 = - b ^ 2 (v + \ textbf {h}) (2 v \ textbf {h} + \ textbf {h} ^ 2)$$

Donde utilicé el hecho de que v es una constante y es independiente del espacio y el tiempo. Luego recordamos que el campo cuántico de Higgs tiene una pequeña amplitud, por lo tanto, al estudiar la única partícula de Higgs (que es exactamente lo que necesitamos para determinar su masa), podemos descartar todos los términos proporcionales a h ² y h ³ :

$$

$$d ^ 2 \ textbf {h} / dt ^ 2 - c ^ 2 d ^ 2 \ textbf {h} / dx ^ 2 = - 2 b ^ 2 v ^ 2 \ textbf {h} + ...$$

Donde "+ ..." recuerda miembros caídos. Tenga en cuenta que esta ecuación para h (x, t) pertenece a la clase 1, aunque comenzamos con una ecuación de clase -1 para H (x, t); Esto se debe a que H (x, t) era inestable en la región de H = 0, y h (x, t) era estable en la región de h = 0, donde H = v. Entonces podemos calcular la masa m _{h de} la partícula de Higgs h usando la siguiente forma de una ecuación de clase 1:

$$

$$m_h = \ sqrt2 (h / 2 \ pi) b v / c ^ 2$$

h en el lado derecho denota la constante de Planck. Si la partícula similar a Higgs que se encontró recientemente en el LHC realmente resulta ser la partícula de Higgs del Modelo Estándar, entonces por primera vez podemos descubrir qué es b (recuerde que v ya lo sabíamos hace mucho tiempo) y finalmente podemos encontrar el valor a = b v.

• v = 246 GeV;
• m _h ≈ 125 GeV / c² (si la nueva partícula es Higgs)
• b ≈ 0.35 (2 π / h) (si la nueva partícula es el Higgs del modelo estándar)
• a = bv ≈ 87 GeV (2 π / h) (si la nueva partícula es el Higgs del modelo estándar)

donde h, de nuevo, es la constante de Planck. Y las últimas tres cantidades no nos eran conocidas hasta el reciente descubrimiento de la partícula de Higgs.

Ahora, si resulta que el Modelo Estándar no corresponde a la naturaleza (si, además de H (x, t), es necesario agregar campos adicionales a los campos conocidos para explicar las propiedades de una partícula descubierta recientemente de masa 125 GeV / c²), supongamos que esta partícula es una de varias tipos de partículas de Higgs, entonces tendremos que lidiar con esta difícil situación en el LHC durante unos años más. Puede imaginar muchas posibilidades, y no tiene sentido explicárselas a todas, pero a grandes rasgos he descrito algunas de ellas aquí; y si los datos recibidos en el LHC nos mostrarán una determinada dirección, le explicaré todo en detalle.