La mecánica clásica es intuitiva: las personas la usan a diario y repetidamente para sobrevivir. Pero hasta el siglo XX, nadie había usado la mecánica cuántica. Ella describe cosas tan pequeñas que se caen completamente de la percepción de los sentidos humanos. La única forma de entender esta teoría, para disfrutar de su belleza, es bloquear nuestra intuición con las matemáticas abstractas.
Leonard Sasskind, un famoso científico estadounidense, te invita a emprender un emocionante viaje al país de la mecánica cuántica. En el camino, necesitará conocimientos básicos del curso de física de la escuela, así como los conceptos básicos de análisis matemático y álgebra lineal. También necesita saber algo sobre los problemas que se abordaron en el primer libro de "mínimo teórico" de Susskind: "Todo lo que necesita saber sobre la física moderna". Pero no tiene miedo si este conocimiento es algo olvidado. Gran parte del autor recordará y explicará en el camino.
La mecánica cuántica es una teoría inusual: según sus postulados, por ejemplo, podemos saber todo sobre el sistema y nada sobre sus partes individuales. Einstein y Niels Bohr discutieron mucho sobre esta y otras contradicciones. Si no le temen a las dificultades, tiene una mente inquisitiva, es técnicamente competente, sinceramente y profundamente interesado en la física, entonces este curso de conferencias de Leonard Sasskind le resultará atractivo. El libro se centra en los principios lógicos de la teoría cuántica y su objetivo no es suavizar la paradoja de la lógica cuántica, sino sacarla a la luz del día y tratar de lidiar con los problemas difíciles que plantea.
Descripción general de la función de onda
En esta conferencia usaremos el lenguaje de las funciones de onda, así que hagamos una breve revisión del material antes de bucear. Discutimos en la clase 5 las funciones de onda de los objetos abstractos, sin explicar cómo se relacionan con las ondas o funciones. Antes de llenar este vacío, les recuerdo lo que discutimos anteriormente.
Para empezar, elegimos una L observable con valores propios l y vectores propios | l〉. Deje | Y〉 ser un vector de estado. Dado que los vectores propios del operador hermitiano forman una base ortonormal completa, el vector | Y〉 puede expandirse de esta manera:
Como recordará de las Secciones 5.1.2 y 5.1.3, las cantidades Y (l) se denominan función de onda del sistema. Pero tenga en cuenta: la forma específica de Y (l) depende del L observable específico que seleccionamos originalmente. Si elegimos otro observable, la función de onda (junto con los vectores de base y los valores propios) resultará ser diferente, a pesar del hecho de que todavía estamos hablando del mismo estado. Por lo tanto, debemos hacer una reserva de que Y (l) es la función de onda asociada con | Yñ. Para ser precisos, debemos decir que Y (l) es la función de onda en la base L. Si utilizamos las propiedades de ortonormalidad de esta base de vectores 〈li | lj〉 = dij, entonces la función de onda en esta base L también se puede definir utilizando los productos internos (o proyecciones) del vector de estado | Y〉 por los vectores propios | l〉: Y (l ) = 〈L | Y〉
Hay dos formas de pensar sobre la función de onda. En primer lugar, este es un conjunto de componentes del vector de estado en una base específica. Estos componentes se pueden escribir en forma de un vector de columna:
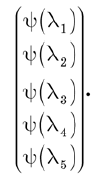
Otra forma de pensar acerca de la función de onda es considerarla como una función de l. Si establece cualquier valor válido de l, entonces la función Y (l) da un número complejo. Por lo tanto, podemos decir que Y (l) es una función de valor complejo de la variable discreta l. Con esta consideración, los operadores lineales se convierten en operaciones que se aplican a funciones y dan nuevas funciones.
Y un último recordatorio más: la probabilidad de que el experimento dé el resultado l es igual a P (l) = Y * (l) Y (l).
Funciones y vectores
Hasta ahora, los sistemas que estudiamos tenían vectores de estado de dimensión finita. Por ejemplo, un giro simple se describe mediante un espacio de estado bidimensional. Por esta razón, los observables tenían solo un número finito de posibles valores observables. Pero hay observables más complejos que pueden tener un número infinito de valores. Un ejemplo es una partícula. Las coordenadas de partículas son observables, pero a diferencia del giro, las coordenadas tienen un número infinito de valores posibles. Por ejemplo, una partícula que se mueve a lo largo del eje x puede estar en cualquier marca de material x. En otras palabras, x es una variable continua infinita. Cuando los sistemas observados son continuos, la función de onda se convierte en una función completa de la variable continua. Para aplicar la mecánica cuántica a sistemas de este tipo, debemos expandir el concepto de vectores para incluir funciones en él.
Las funciones son funciones y los vectores son vectores; parecen ser entidades completamente diferentes, entonces, ¿en qué sentido son vectores de funciones? Si piensa en los vectores como flechas en el espacio tridimensional, entonces, por supuesto, no son lo mismo que las funciones. Pero si observa los vectores de manera más amplia, como en los objetos matemáticos que satisfacen algunos postulados, las funciones en realidad forman un espacio vectorial. Tal espacio vectorial a menudo se llama un espacio de Hilbert en honor del matemático David Hilbert.
Considere el conjunto de funciones complejas Y (x) de una variable real x. Por una función compleja, quiero decir que a cada x asocia un número complejo Y (x). La variable independiente x, por otro lado, es una variable real ordinaria. Puede tomar cualquier valor real de –∞ a + ∞.
Ahora declaramos exactamente lo que queremos decir al decir que "las funciones son vectores". Esta no es una analogía o metáfora superficial. Bajo algunas restricciones (a las que volveremos más adelante), funciones como Y (x) satisfacen los axiomas matemáticos que definen un espacio vectorial. Mencionamos brevemente esta idea en la sección 1.9.2, y ahora la usamos con toda su fuerza. Mirando hacia atrás a los axiomas de un espacio vectorial complejo (en la Sección 1.9.1), vemos que las funciones complejas los satisfacen a todos.
1. La suma de cualquiera de las dos funciones es una función.
2. La adición de funciones es conmutativa.
3. La adición de funciones es asociativa.
4. Existe una función cero única, de modo que cuando se agrega a cualquier función, se obtiene la misma función.
5. Para cualquier función dada Y (x), hay una función única –Y (x) tal que Y (x) + (–Y (x)) = 0.
6. La multiplicación de una función por cualquier número complejo da una función y es lineal.
7. Se observa la propiedad de distribución, lo que significa que
z [Y (x) + j (x)] = zY (x) + zj (x),
[z + w] Y (x) = zY (x) + wY (x),
donde z y w son números complejos.
Todo esto implica que podemos identificar la función Y (x) con el vector ket | Y〉 en el espacio vectorial abstracto. No es sorprendente que también podamos definir vectores de bra. El vector bra 〈Y | correspondiente a la sal de chum | Y〉 se identifica con la función conjugada compleja Y * (x).
Para usar esta idea de manera efectiva, necesitamos generalizar algunos objetos de nuestro conjunto de herramientas matemáticas. En conferencias anteriores, las etiquetas que identificaban funciones de onda eran miembros de un conjunto discreto finito, por ejemplo, los valores propios de un determinado observable. Pero ahora la variable independiente es continua. Entre otras cosas, esto significa que no podemos resumirlo usando cantidades ordinarias. Creo que sabes que hacer. Aquí hay sustitutos orientados a funciones para nuestros tres conceptos vectoriales, dos de los cuales ya está familiarizado.
• Las cantidades se reemplazan por integrales.
• Las probabilidades se reemplazan por densidades de probabilidad.
• El símbolo delta de Kronecker se reemplaza por la función delta de Dirac.
Echemos un vistazo más de cerca a estas herramientas.
Las cantidades se reemplazan por integrales . Si realmente quisiéramos mantener el rigor, comenzaríamos por reemplazar el eje x con un conjunto discreto de puntos separados por intervalos muy pequeños ε, y luego pasar al límite ε → 0. Se necesitarían varias páginas para justificar cada paso. Pero podemos evitar esta molestia con algunas definiciones intuitivas, como reemplazar sumas por integrales. Esquemáticamente, este enfoque se puede escribir de la siguiente manera:
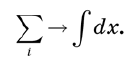
Por ejemplo, si necesita calcular el área bajo la curva, el eje x se divide en pequeños segmentos, luego se suman las áreas de una gran cantidad de rectángulos, como en un análisis matemático elemental. Cuando dejamos que los segmentos se contraigan al tamaño cero, la suma se convierte en una integral.
Considere la llave 〈Y | y ket | Y〉 y definen su producto interno. La forma obvia de hacer esto es reemplazar la suma en la ecuación (1.2) con integración. Definimos el producto interno de la siguiente manera:
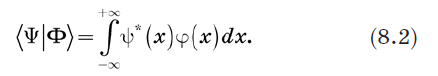Las probabilidades se reemplazan por densidades de probabilidad . A continuación, identificamos P (x) = Y * (x) Y (x) con la densidad de probabilidad para la variable x. ¿Por qué con densidad de probabilidad, y no solo con probabilidad? Si x es una variable continua, entonces la probabilidad de que tome cualquier valor dado es generalmente cero. Por lo tanto, es más correcto plantear la pregunta de esta manera: ¿cuál es la probabilidad de que x se encuentre entre dos valores x = a y x = b? La densidad de probabilidad se determina de modo que esta probabilidad esté dada por la integral
Como la probabilidad total debe ser 1, podemos definir la normalización del vector como
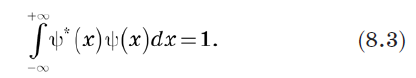El símbolo delta de Kronecker se reemplaza por la función delta de Dirac . Hasta ahora, todo ha sido muy familiar. La función Delta de Dirac es algo nuevo. La función delta es un análogo del símbolo delta de Kronecker dij, que por definición es 0 si i ≠ j, y 1 si i = j. Pero se puede definir de otra manera. Considere cualquier vector Fi en un espacio de dimensión finita. Es fácil ver que el símbolo delta de Kronecker satisface la condición
Esto se debe al hecho de que solo los términos con j = i no son cero en esta suma. Durante la suma, el símbolo de Kronecker filtra todos los componentes de F excepto Fi. Una generalización obvia de esto será definir una nueva función que tenga la misma propiedad de filtrado cuando se use bajo la integral. En otras palabras, necesitamos una nueva entidad d (x - x '), que tenga la propiedad de que para cualquier función F (x)
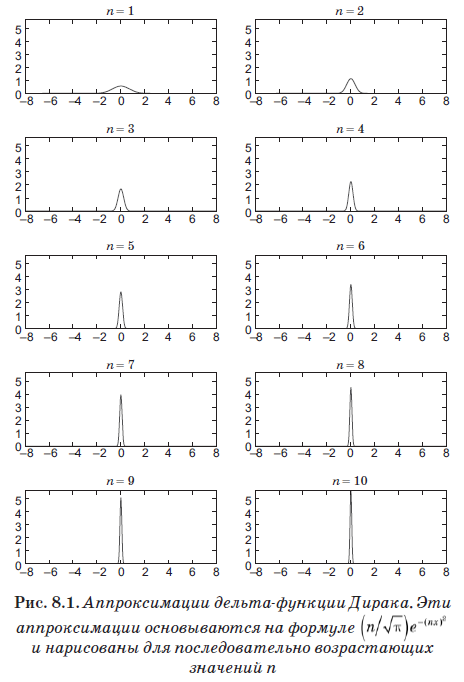
La ecuación (8.4) define una nueva entidad llamada función delta de Dirac, que resultó ser la herramienta más importante en la mecánica cuántica. Pero a pesar de su nombre, esta no es realmente una función en el sentido habitual. Es igual a cero donde x ≠ x ', pero cuando x = x' va al infinito. De hecho, es infinita lo suficiente para que el área debajo de d (x) sea igual a 1. Hablando en términos generales, esta función no es cero en el intervalo infinitamente pequeño ε, pero en este intervalo tiene el valor 1 / ε. Por lo tanto, el área debajo de ella es igual a 1 y, lo que es más importante, satisface la ecuación (8.4). Función
aproxima bastante bien la función delta para valores muy grandes de n. En la fig. 8.1 muestra esta optimización con valores crecientes de n. A pesar de que nos decidimos por n = 10, es decir, un valor muy pequeño, tenga en cuenta que el gráfico ya se ha convertido en un pico muy estrecho y agudo.
»Se puede encontrar más información sobre el libro en
el sitio web del editor»
Contenidos»
ExtractoPara los lectores de este blog, un descuento del 20% en el cupón -
Sasskind