El libro "Mínimo teórico. Todo lo que necesitas saber sobre física moderna ”

"Mínimo teórico" es un libro para aquellos que perdieron lecciones de física en la escuela y el instituto, pero ya lo lamenta. ¿Desea comprender los conceptos básicos de las ciencias naturales y aprender a pensar y razonar como lo hacen los físicos modernos? En forma original y no estándar, los famosos científicos estadounidenses Leonard Sasskind y George Grabowski ofrecen un curso introductorio de matemáticas y física para mentes curiosas.

A diferencia de otros libros de ciencias populares que intentan explicar las leyes de la física de una manera accesible, evitando hábilmente ecuaciones y fórmulas, los autores enseñan al lector los fundamentos clásicos de las ciencias naturales. El libro ofrece su propia metodología de enseñanza original, complementada por conferencias en video publicadas en teóricaminimum.com .

Lección 9. Fluido de fase y el teorema de Gibbs - Liouville

A Lenny le gustaba mirar el río, especialmente para observar las pequeñas motas flotando en la superficie. Trató de imaginar cómo se moverían entre piedras o cayendo en remolinos. Pero el curso del río en su conjunto (el movimiento combinado de un gran volumen de agua, con corrientes que se separan, convergen y se superan) estaba más allá de su comprensión.

Fluido de fase

Concentrarse en condiciones iniciales específicas y seguir una trayectoria separada en el espacio de fase es muy natural para la mecánica clásica. Pero también hay una visión más amplia que cubre toda una familia de trayectorias. En lugar de colocar la punta del lápiz en un cierto punto en el espacio de fase y trazar el único camino desde allí, intentaremos hacer algo más ambicioso. Imagine que tenemos un número infinito de lápices y utilícelos para llenar uniformemente el espacio de fase con puntos (por homogeneidad, quiero decir que la densidad de puntos en el espacio q, p es la misma en todas partes). Considere estos puntos como partículas que forman un fluido imaginario que llena el espacio de fase.

Ahora deje que cada punto se mueva de acuerdo con las ecuaciones de movimiento de Hamilton:


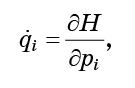
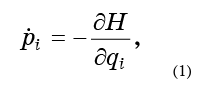
para que nuestro fluido fluya sin fin a través del espacio de fase.

Un oscilador armónico es un buen ejemplo inicial. En la lección 8, vimos que cada punto se mueve en una órbita circular con una velocidad angular constante. (Permítanme recordarles que estamos hablando de fase, no de espacio de coordenadas. En coordenadas, el oscilador se mueve hacia adelante y hacia atrás en una dimensión). Todo el fluido en su conjunto hace un movimiento sólido, girando uniformemente alrededor del origen del espacio de fases.

Ahora volviendo al caso general. Si el número de coordenadas es N, entonces el espacio de fase y el líquido en él son de 2N dimensiones. El fluido fluye, pero de una manera muy específica. Su flujo tiene propiedades especiales. Una de ellas es que si un punto comienza con una cierta energía, es decir, para un valor dado de H (q, p), entonces almacena este valor de energía. Las superficies de energía constante (por ejemplo, con energía igual a E) están determinadas por la ecuación H (q, p) = E. (2)

Para cada valor de E, tenemos una ecuación con variables de espacio de fase 2N que define una superficie de dimensión 2N - 1. En otras palabras, cada valor de E tiene su propia superficie; Cuando revisa todos los valores de E, estas superficies llenan todo el espacio de fase. Podemos considerar el espacio de fase con las superficies dadas por la ecuación (2) como un mapa de contornos (Fig. 1), en el que las horizontales representan no la altura, sino los valores de energía. Si el punto líquido está en una superficie específica, permanecerá en él para siempre. Esta es la ley de conservación de la energía.

El espacio de fase del oscilador armónico es bidimensional, y las superficies de energía son círculos:

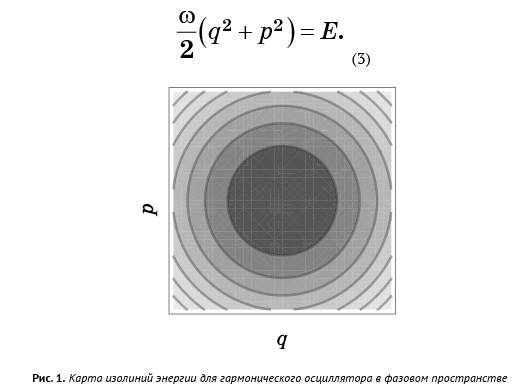
En el caso general, las superficies de energía de un sistema mecánico son demasiado complicadas para visualizarlas, pero el principio sigue siendo el mismo: las superficies de energía llenan el espacio de fase como capas, y el flujo se mueve para que los puntos permanezcan en la superficie en la que estaban originalmente .

Breve recordatorio

Me gustaría detenerme aquí y recordar lo que se dijo en la primera conferencia, donde se discutieron monedas, dados y las ideas más simples sobre las leyes del movimiento. Describimos estas leyes con un conjunto de flechas que conectan los puntos que representan los estados del sistema. También explicamos que las leyes son admisibles e inadmisibles, mientras que las admisibles son reversibles. La conclusión es que cada punto debe tener exactamente una flecha entrante y exactamente una flecha saliente. Si al menos en un punto el número de flechas entrantes excede el número de salientes (esto se llama convergencia), entonces dicha ley es irreversible. Lo mismo se aplica al caso cuando hay más flechas salientes que entrantes (esto se llama divergencia). Tanto la divergencia como la convergencia de flechas violan la reversibilidad y están prohibidas. Hasta ahora, no hemos vuelto a esta línea de razonamiento. Ahora ha llegado el momento.

Flujo y divergencia

Considere algunos ejemplos simples de flujo de fluidos en el espacio ordinario. Por un momento, nos olvidamos del espacio de fase y solo consideramos un fluido ordinario que se mueve en el espacio tridimensional habitual con ejes denotados como x, y, z. El flujo puede ser descrito por el campo de velocidad . Campo de velocidad

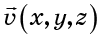
se determina configurando el vector de velocidad en cada punto del espacio (Fig. 2).

También puede describir el campo de velocidad con componentes de velocidad:

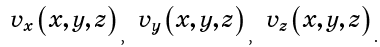
Además, la velocidad en un punto puede depender del tiempo, pero supongamos que no existe tal dependencia. En este caso, el flujo se llama estacionario .

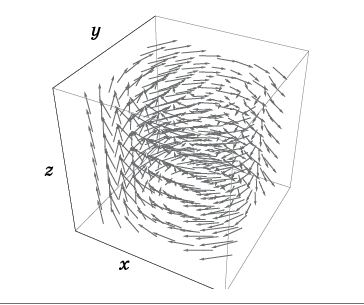
Fig. 2. Campo de velocidad

toma la misma cantidad También significa que la densidad de un fluido (la cantidad de moléculas por unidad de volumen) es la misma en todas partes y es constante en el tiempo. Por cierto, el término "incompresibilidad" también significa inextensibilidad. En otras palabras, el líquido no puede aumentar de volumen. Considere una pequeña celda cúbica definida por las condiciones:

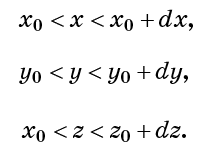
La incompatibilidad implica que el número de puntos de fluido en cada celda es constante. Esto también significa que el flujo total de fluido que ingresa a la celda (por unidad de tiempo) debe ser cero. (Cuántos puntos del flujo entran, sale el mismo número). Considere el número de moléculas que pasan por unidad de tiempo a través de la superficie celular x = x0. Será proporcional a la velocidad de flujo en esta superficie vx (x0).

Si la velocidad vx es la misma en x0 y en x0 + dx, entonces el flujo hacia la celda a través de x = x0 será el mismo que el flujo desde x a través de x = x0 + dx. Pero si vx cambia en toda la célula, estos dos flujos estarán desequilibrados. El flujo total que ingresa a la celda a través de estas dos caras será proporcional

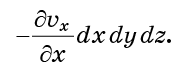
Exactamente las mismas consideraciones se aplican a las caras y0 e y0 + dy, así como a z0 y z0 + dz. Si se agregan todos, entonces el flujo total de moléculas en la célula (entrada menos salida)

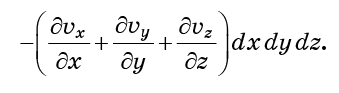
La combinación de derivadas entre paréntesis se denomina divergencia del campo vectorial.
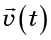
y es designado

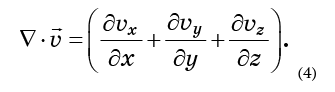
La divergencia refleja el grado de dispersión de las moléculas, o el aumento en el volumen ocupado por ellas. Si el fluido es incompresible, este volumen no debería cambiar, lo que significa que la divergencia debería ser cero.

Una forma de entender la incompresibilidad es imaginar que cada molécula o punto ocupa un volumen que no se puede cambiar. No se pueden comprimir en un volumen más pequeño, no desaparecen y no aparecen de la nada. Con un poco de reflexión, puede ver cuán incompresibles y reversibles son similares. En los ejemplos que analizamos en la clase 1, las flechas también determinaron un tipo de flujo. Y esencialmente esta corriente era incompresible, al menos si era reversible. La pregunta natural que se deduce de esto es: ¿es reversible el flujo en el espacio de fase? La respuesta es sí, si el sistema satisface las ecuaciones de Hamilton. Y el teorema que expresa esta incompresibilidad se llama teorema de Liouville.

Teorema de Liouville

Regresemos al flujo de fluido en el espacio de fase y consideremos los componentes de la velocidad del fluido en cada punto del espacio de fase. No es necesario decir que el fluido de fase no es tridimensional en las coordenadas x, y, z. Es un fluido de 2N dimensiones en las coordenadas pi, qi.

Por lo tanto, hay 2N componentes del campo de velocidad: uno para cada coordenada q y cada coordenada p. Dejarlos

El concepto de divergencia expresado por la ecuación (4) se generaliza fácilmente a cualquier número de dimensiones. En tres dimensiones, esta es la suma de las derivadas de los componentes de velocidad en las direcciones correspondientes. Del mismo modo, se determina para cualquier cantidad de dimensiones. En el caso del espacio de fases, la divergencia del flujo es la suma de 2N miembros:

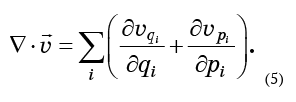
Si el fluido es incompresible, entonces esta expresión debería ser cero. Para calcularlo, debe conocer los componentes del campo de velocidad; por supuesto, no son más que las velocidades de las partículas del fluido de fase.

El vector de flujo en un punto dado se identifica con la velocidad de una partícula imaginaria en ese punto. En otras palabras

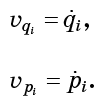
Por otra parte
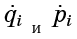
- Estas son solo las cantidades que entran en las ecuaciones de Hamilton (1):


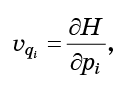
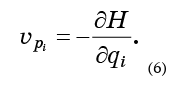
Todo lo que hay que hacer es sustituir las ecuaciones (6) en la fórmula (5) y obtener

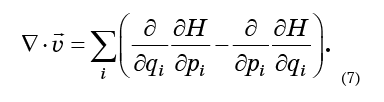
Recordando que la segunda derivada de la forma


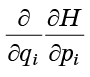
no depende del orden de diferenciación, entenderemos que los términos de la ecuación (7) se destruyen exactamente en pares:


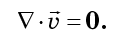
Entonces, el fluido de fase es incompresible. En la mecánica clásica, la incompresibilidad de un fluido de fase se llama teorema de Liouville, aunque casi no tiene relación con el matemático francés Joseph Liouville. Fue publicado por primera vez en 1903 por el gran físico estadounidense Josiah Willard Gibbs, y también se conoce como el teorema de Gibbs-Liouville.

Determinamos la incompresibilidad de un fluido al exigir que la cantidad total de fluido que ingresa a cualquier celda pequeña sea cero. Hay otra definición estrictamente equivalente. Imagine un volumen de líquido en algún momento. Este volumen puede tener cualquier forma: esférica, cúbica, en forma de gota, lo que sea. Ahora seguiremos el movimiento de todos los puntos de este volumen. Después de un tiempo, una gota de líquido estará en un lugar diferente y tendrá una forma diferente. Pero si el fluido es incompresible, el volumen de la gota seguirá siendo el mismo que originalmente. Entonces podemos reformular el teorema de Liouville: el volumen ocupado por una gota de líquido de fase se conserva en el tiempo .

Considere un ejemplo de un oscilador armónico en el que un fluido gira alrededor de un punto de referencia. Obviamente, la caída retiene el volumen, ya que todo su movimiento se reduce a la rotación en estado sólido. La forma de la caída permanece sin cambios, pero este es el caso del oscilador armónico. Considere otro ejemplo. Supongamos que el hamiltoniano tiene la forma H = pq.

Quizás esto te parezca diferente al hamiltoniano, aunque es completamente correcto. Derivamos las ecuaciones de movimiento:

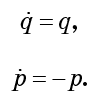
De acuerdo con estas ecuaciones, q aumenta exponencialmente con el tiempo y p disminuye exponencialmente con la misma velocidad. En otras palabras, el flujo presiona el fluido contra el eje p, mientras que simultáneamente lo expande a lo largo del eje q en la misma medida. Cualquier caída se extiende a lo largo de q y se contrae a lo largo de p. Obviamente, la caída experimenta enormes deformaciones, pero su volumen de fase no cambia.

El teorema de Liouville es el análogo imaginable más cercano del tipo de irreversibilidad que discutimos en la Lección 1. En la mecánica cuántica, el teorema de Liouville se reemplaza por una versión cuántica llamada unitaridad. La unitaridad es aún más similar a lo que discutimos en la conferencia 1, pero este es el tema del próximo número de The Theoretical Minimum.

»Se puede encontrar más información sobre el libro en el sitio web del editor
» Exclamación
» Extracto

Para los lectores de este blog, un descuento del 20% en el cupón: mínimo teórico