Después de haber vertido arena sobre una placa elástica oscilante, se puede ver la formación de figuras de Hladni . A menudo sirven como un ejemplo de la "belleza natural" de los fenómenos físicos, aunque detrás de ellos está la física bastante simple de la excitación resonante de las ondas estacionarias. Y pocas personas prestan atención a la característica curiosa de estas figuras: las líneas en ellas evitan las intersecciones, como si alguna fuerza las repele. Tratemos de entender qué tipo de física se esconde detrás de esta repulsión y cómo se relaciona con la teoría cuántica del caos.

Ondas estacionarias

Como sabemos, los cuerpos elásticos pueden hacer vibraciones bastante complejas, durante las cuales se contraen, estiran, doblan y tuercen. Sin embargo, las vibraciones de cualquier cuerpo elástico pueden representarse como una combinación de vibraciones normales más simples superpuestas entre sí. Así es como se ven varias vibraciones normales de un cuerpo elástico simple, una cuerda estirada unidimensional.

Cada oscilación normal está representada por una onda estacionaria , que, a diferencia de una onda viajera, se detiene y tiene su propio patrón de distribución de las amplitudes de las oscilaciones en el espacio. En esta figura, se pueden distinguir los antinodos (puntos donde la amplitud de las oscilaciones alcanza los máximos y nodos) , puntos fijos en los que la amplitud de las oscilaciones es cero. Además, cada onda oscila con su propia frecuencia . En el caso de una cuerda, como puede ver, la frecuencia de las oscilaciones de una onda estacionaria aumenta a medida que aumenta el número de nodos y antinodos.


Veamos ahora un sistema bidimensional, un ejemplo del cual es una delgada membrana elástica estirada sobre un marco rígido. Las vibraciones normales de una membrana redonda parecen más complicadas que en el caso de una cuerda, y en lugar de puntos-nodos individuales hay líneas nodales a lo largo de las cuales la membrana es estacionaria.


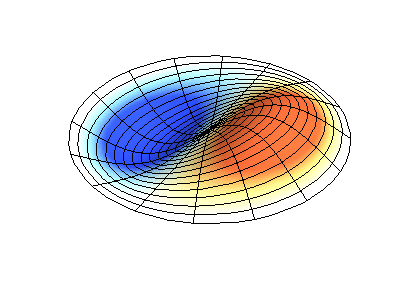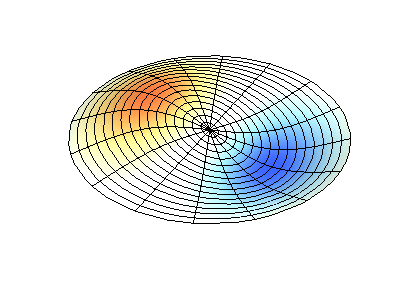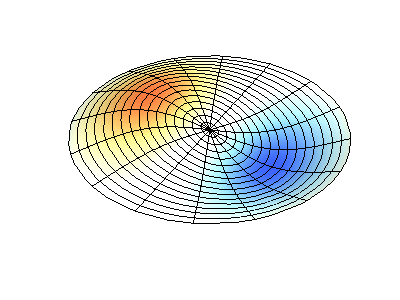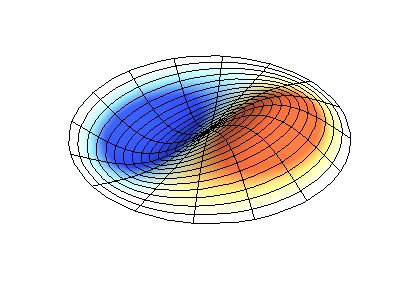
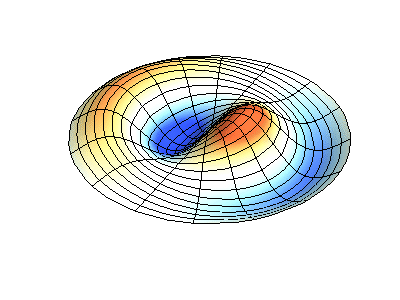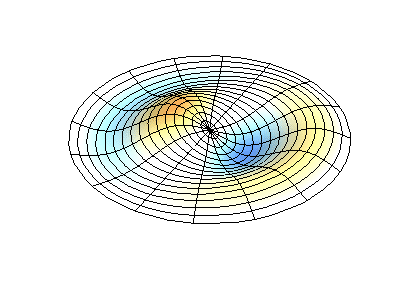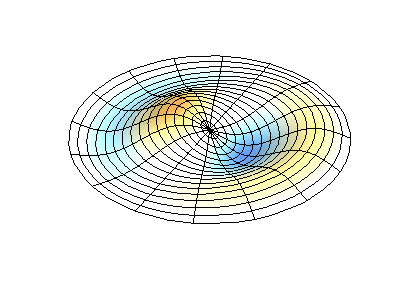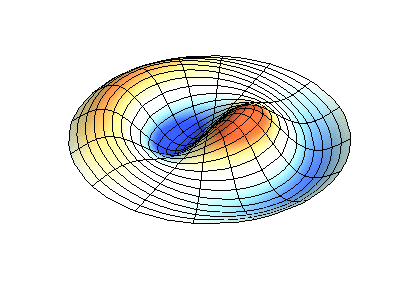
Vibraciones normales de una membrana redonda con bordes fijos. Fuente


El color verde muestra líneas nodales.

En una membrana redonda, las líneas nodales, que son círculos y segmentos a lo largo de los radios, pueden cruzarse en ángulo recto. Si los bordes de la membrana tienen una forma arbitraria, encontrar las frecuencias de vibraciones y patrones normales de sus nodos y antinodos se convierte en un problema que solo puede resolverse usando una computadora.

Perfiles de la amplitud de las oscilaciones de las ondas estacionarias en las membranas en forma de un cuadrado con un agujero , copos de nieve Koch y superficie de gatito .

Las ecuaciones que describen las vibraciones de una placa elástica delgada difieren de las ecuaciones de oscilación de la membrana, ya que la placa tiene su propia rigidez, mientras que la membrana es suave y elástica solo debido a la tensión por fuerzas externas. Sin embargo, también existen conjuntos de vibraciones normales, cuyos dibujos dependen sustancialmente de la forma de los límites.

Figuras Hladni

Como se mencionó anteriormente, en el caso general, las vibraciones corporales son una combinación de un conjunto completo de vibraciones normales excitadas en él. El fenómeno de resonancia le permite excitar selectivamente una de las vibraciones normales que necesitamos, para esto necesitamos balancear el cuerpo usando una fuerza externa con una frecuencia igual a la frecuencia natural de la oscilación normal.

Los dos videos a continuación muestran un esquema típico para obtener figuras de Hladni: una placa elástica está unida en el centro a un generador de vibraciones mecánicas, cuya frecuencia aumenta gradualmente. Las vibraciones normales de la placa con sus patrones de nodos y antinodos se excitan cuando la frecuencia del oscilador coincide de manera resonante con las frecuencias naturales de estas vibraciones (las frecuencias naturales se muestran en el video en la esquina inferior izquierda).

Aquí está la versión del mismo video en el que las frecuencias de las vibraciones normales se pueden estimar por oído.

Y aquí está un poco más bonito.

Vemos patrones de nudos y antinodos debido al hecho de que las corrientes de aire cerca de una placa oscilante soplan granos de arena hacia las líneas nodales de una onda estacionaria ^(*) Así, las figuras de Hladni nos muestran patrones de líneas nodales de vibraciones normales de una placa elástica.

Varias figuras de Hladni en la cubierta superior de la guitarra. Fuente

Otro ejemplo de ondas normales son las ondas estacionarias en la superficie del agua. Se describen mediante una ecuación que difiere de las ecuaciones de vibración de las placas y las membranas, pero siguen las mismas leyes cualitativas, y con su ayuda es posible obtener análogos de las figuras de Hladni.

Micropartículas en la superficie del agua en recipientes de varias formas. La línea negra muestra una escala de 2 milímetros. Fuente

Caos clásico

¡Entonces, vimos que en el caso de una membrana redonda, las líneas nodales son teóricamente! - se cruzan notablemente, al mismo tiempo, en las figuras de Hladni en placas cuadradas o más complejas, las líneas nodales evitan las intersecciones. Para comprender la razón de estos patrones, tendremos que hacer una pequeña excursión a la teoría del caos.

El caos clásico es una propiedad de los sistemas mecánicos, que consiste en una dependencia extremadamente fuerte de la trayectoria de su movimiento de los cambios en las condiciones iniciales. Esta relación también se conoce como el " efecto mariposa ". Se puede encontrar un ejemplo vívido de comportamiento caótico en los intentos de predecir el clima: el sistema de ecuaciones que describe el movimiento de la atmósfera y los océanos no permite que se realicen pronósticos suficientemente precisos en tiempos prolongados debido a errores que aumentan exponencialmente debido a pequeñas inexactitudes en los datos iniciales ^(**)

El fenómeno del caos fue abierto y popularizado por el meteorólogo y matemático Edward Lorenz , quien descubrió que dos cálculos de pronóstico del tiempo que comienzan con condiciones iniciales muy cercanas eran inicialmente casi indistinguibles, pero en algún momento comenzaron a divergir radicalmente.

Dos cálculos de Edward Lorenz, a partir de valores iniciales cercanos 0.506 y 0.506127. Fuente

Los sistemas más simples, en cuyo ejemplo es conveniente estudiar el caos, son los billares : secciones de una superficie plana a lo largo de las cuales una bola puede rodar sin fricción, rebotando elásticamente en paredes rígidas. En el billar caótico, las trayectorias de la pelota, que tienen ligeras diferencias al principio, posteriormente divergen significativamente. Un ejemplo de billar caótico es el billar del Sinaí que se muestra a continuación, que es una piscina rectangular con un obstáculo circular en el centro. Como veremos, es precisamente debido a este obstáculo que el billar se vuelve caótico.

Dos trayectorias de pelota exponencialmente divergentes en el billar del Sinaí. Fuente

Sistemas integrales y caóticos.

Los sistemas mecánicos que no son caóticos se denominan integrables , y con el ejemplo del billar, puede ver claramente la diferencia entre sistemas integrables y caóticos.

Los billares rectangulares y redondos son integrables debido a su forma simétrica. ^(***) El movimiento de la pelota en tales billares es simplemente una combinación de dos movimientos periódicos independientes. En el billar rectangular, estos son movimientos con rebotes de las paredes horizontal y verticalmente, y de manera redondeada se trata de movimiento a lo largo del radio y movimiento angular en un círculo alrededor del centro. Tal movimiento se calcula fácilmente y no muestra un comportamiento caótico.

Trayectorias de bolas en billar integrable.

Los billares de una forma más compleja, que no poseen una simetría tan alta como un círculo o rectángulo, son caóticos. ^(****) Uno de ellos que vimos arriba es el billar del Sinaí, en el cual la simetría del rectángulo es destruida por una inclusión circular en el centro. También a menudo se consideran billar "estadio" y billar en forma de caracoles Pascal. La pelota se mueve en billar caótico a lo largo de caminos muy complicados y no se descompone en movimientos periódicos más simples.

La trayectoria del balón en el caótico billar "estadio" y "caracol Pascal".

Aquí ya puedes adivinar que la presencia de intersecciones entre las líneas en las figuras de Hladni está determinada por si la placa tiene la forma de un billar integrable o caótico. Esto se ve claramente en las fotos a continuación.

Placas redondas Hladni, que demuestran las propiedades de billar integrado. Fuente

Demostrando las propiedades de los caóticos billares del plato Hladni en forma de billar "estadio", el caso del violín y el cuadrado, cuya simetría se rompe por un dispositivo redondo en el centro (análogo de billar Sinaí). Fuente

Caos cuántico

¿Cómo entender por qué las intersecciones entre líneas nodales se deben a la integrabilidad del billar? Para hacer esto, necesitamos recurrir a la teoría cuántica del caos , combinando la teoría del caos con la mecánica de las oscilaciones y las ondas. Si en la mecánica clásica la pelota en el billar se describe como un punto material que se mueve a lo largo de una cierta trayectoria, entonces en la mecánica cuántica su movimiento se describe como la propagación de una onda que obedece a la ecuación de Schrödinger y se refleja desde las paredes del billar.

Etapas de propagación de ondas en billar cuántico. Inicialmente, la onda se concentra en un pulso redondo y se mueve de izquierda a derecha, luego se extiende y se refleja repetidamente desde las paredes. Fuente

Lo mismo en forma de animación, pero con condiciones iniciales ligeramente diferentes.

Como en el caso de las vibraciones de membranas y placas, la ecuación de Schrödinger que describe el billar cuántico permite encontrar vibraciones normales en forma de ondas estacionarias, que tienen un patrón característico de líneas nodales y antinodos, individuales para cada oscilación y dependiendo de la forma de los límites.

Ejemplos de perfiles de amplitudes de oscilaciones en ondas estacionarias en billar cuántico caótico " Caracol de Pascal " y " estadio ".

Los patrones de ondas estacionarias en billar cuántico integrable y caótico son cualitativamente diferentes: los billares integrables muestran patrones simétricos y ordenados de ondas estacionarias, mientras que en los billares caóticos los patrones de ondas estacionarias son muy confusos y no muestran ningún patrón visible (al final del artículo se mostrará que algunos interesantes patrones todavía existen).

Las amplitudes de oscilación en las ondas estacionarias de un billar redondo integrable (fila superior) y billar caótico en forma de un caracol Pascal (fila inferior). Fuente

Las imágenes extrañas de vibraciones normales en billar caótico a veces sirven como tema de un estudio separado. Fuente

También se observa una diferencia cualitativa en los patrones de las líneas nodales: en el caso del billar cuántico integrable, vemos familias ordenadas de líneas que se cruzan entre sí , y en el billar caótico, estas líneas, por regla general, no se cruzan .

Arriba: líneas nodales (líneas negras entre las áreas azul y roja) de ondas estacionarias de billar integrales, redondos y rectangulares. Abajo: las líneas nodales de una de las ondas estacionarias en los caóticos billares: una cuarta parte de los billares del estadio .

¿Se cruzan o no se cruzan?

¿Por qué las líneas nodales en billar caótico no se cruzan? En 1976, la matemática Karen Uhlenbeck demostró un teorema según el cual las líneas nodales de ondas estacionarias de billar cuántico, en general, no deberían cruzarse.

En una forma simplificada, esto se puede mostrar de la siguiente manera: suponga que dos líneas nodales se cruzan en un punto ( x ₀ , y ₀ ). Para que esto suceda, la función f ( x, y ), que determina la dependencia de la amplitud de la onda estacionaria en las coordenadas, debe satisfacer simultáneamente tres condiciones:

1) Debe ser igual a cero en el punto ( x ₀ , y ₀ ), ya que este punto es nodal.
2) Si se mueve desde el punto ( x ₀ , y ₀ ) en la dirección de la primera línea nodal, entonces f ( x, y ) debe permanecer igual a cero.
3) Si se mueve desde el punto ( x ₀ , y ₀ ) en la dirección de la segunda línea nodal, entonces f ( x, y ) también debe permanecer igual a cero.


En total, tenemos tres condiciones (o tres ecuaciones) impuestas sobre la función de dos variables f ( x, y ). Como sabemos, una ecuación no es suficiente para encontrar completamente las dos incógnitas x e y , dos ecuaciones ya son suficientes para esto, y tres ecuaciones son demasiado. El sistema de tres ecuaciones para dos incógnitas, en general, no tendrá soluciones, a menos que tengamos la suerte. Por lo tanto, los puntos de intersección de las líneas nodales pueden existir solo como una excepción .

En el billar integrable, tales excepciones simplemente surgen. Como vimos anteriormente, sus propiedades especiales (previsibilidad de movimiento, ausencia de caos, patrones regulares de ondas estacionarias) son el resultado de su alta simetría. La misma simetría asegura el cumplimiento simultáneo de tres condiciones necesarias para las intersecciones de líneas nodales.

Echemos ahora un vistazo más de cerca a ejemplos de figuras de Hladni típicas de billar integrable y caótico. La siguiente figura muestra tres casos característicos . A la izquierda, la placa tiene la forma de un círculo, por lo que el billar cuántico correspondiente es integrable, y las líneas nodales se cruzan entre sí. En el centro, la placa es rectangular, lo que también corresponde a un sistema integrable, sin embargo, el montaje redondo en el centro viola ligeramente la simetría del rectángulo, por lo que las líneas nodales no se cruzan en todas partes. Un ejemplo de un sistema puramente caótico se muestra a la derecha: una placa en forma de una cuarta parte del billar del Sinaí (en la esquina superior derecha hay un corte circular), las líneas nodales en las que ya no se cruzan.



Por lo tanto, cuanto más fuerte sea la forma de la placa, teniendo en cuenta su fijación, difiere de la forma de un billar integrado (como un círculo o un rectángulo), menos intersecciones de líneas nodales en ella .

No es tan fácil obtener hermosas figuras de Hladni con líneas que se cruzan en un plato redondo. Cuando las vibraciones excitantes con una fijación central, la simetría circular de todo el sistema prohíbe la formación de líneas nodales radiales, por lo que solo veremos un conjunto aburrido de círculos (esta dificultad puede evitarse vibraciones excitantes no desde el centro, sino desde el borde de la placa usando el arco del violín). Si la placa se fija fuera del centro, las figuras de Hladni se volverán más interesantes, pero debido a la violación de la simetría circular, el sistema dejará de ser integrable.

Placa redonda, montaje central.

Placa redonda, montaje desplazado desde el centro.

Y aquí hay diferentes opciones con placas redondas y no circulares.

Finalmente, un lector atento puede notar: pero veo que a veces las líneas nodales se cruzan incluso en placas "caóticas". ¿Cómo es que si su intersección está prohibida por el teorema de Uhlenbeck?

En primer lugar, las líneas nodales pueden evitar la intersección, pero antes de eso se acercan tanto que, debido al ancho finito del camino de arena, nos parecerá que hay una intersección. En segundo lugar, entre los sistemas integrables y caóticos, de hecho, no existe un límite definido.

Líneas nodales - separan áreas en blanco y negro - en billar cuántico integrable y caótico (izquierda y derecha), y en el caso pseudo-integrable intermedio (en el centro). En el caso intermedio, hay varias intersecciones de las líneas nodales, mientras que en el caso caótico no hay ninguna. Fuente

En la teoría clásica del caos, la famosa teoría de Kolmogorov-Arnold-Moser está dedicada a este tema. Ella dice que si se viola ligeramente la simetría del sistema integrable, no exhibirá inmediatamente un comportamiento caótico, pero, en su mayor parte, mantendrá su previsibilidad de movimiento. Al nivel de la teoría cuántica del caos y las figuras de Hladni, esto se manifiesta en el hecho de que en algunos lugares se preservan las intersecciones de líneas nodales. Esto ocurre en puntos particularmente simétricos del billar o lejos de la fuente de perturbación, lo que viola la simetría del sistema integrable.

Que mas

¿Qué más es interesante en la teoría cuántica del caos? Para el lector interesado, mencionaré tres preguntas adicionales que ya no están directamente relacionadas con las figuras de Hladni.

1) Un fenómeno importante estudiado por esta teoría es la universalidad de los sistemas caóticos. La gran mayoría de los sistemas en los que pueden ocurrir vibraciones normales son caóticos, y todos ellos, ¡independientemente de su naturaleza física! - obedecer las mismas leyes. El fenómeno de la universalidad, en el que se describen sistemas completamente diferentes mediante las mismas fórmulas, es en sí mismo muy hermoso y sirve como un recordatorio de la unidad matemática del mundo físico.

Estadísticas de distancias entre frecuencias adyacentes de vibraciones normales en sistemas caóticos de diferente naturaleza física, en todas partes descritas por la misma fórmula universal de Wigner-Dyson. Fuente

2) Los patrones de vibraciones normales de billar caótico tienen una característica interesante llamada "cicatrices cuánticas" . Hemos visto que los caminos de la pelota en el billar caótico generalmente se ven muy confusos. Pero hay excepciones: estas son órbitas periódicas , trayectorias cerradas bastante simples y cortas a lo largo de las cuales la pelota hace movimientos periódicos. Las cicatrices cuánticas se llaman espesamiento agudo de las ondas estacionarias a lo largo de órbitas periódicas.

Cicatrices cuánticas en el "estadio" de billar, que recorren las órbitas periódicas que se muestran con líneas rojas y verdes. Fuente

3) Hasta ahora hemos hablado de sistemas bidimensionales. Si consideramos la propagación de ondas en el espacio tridimensional, entonces también pueden surgir líneas nodales a lo largo de las cuales la amplitud de oscilación es cero. Esto es especialmente importante cuando se estudia la condensación y superfluidez de Bose, donde miles de átomos se mueven como " ondas de materia ". Es necesario un análisis de la estructura de las líneas nodales de ondas de materia en el espacio tridimensional, por ejemplo, para comprender cómo surge y se desarrolla la turbulencia cuántica en los sistemas superfluidos.

Estructuras tridimensionales enredadas de líneas nodales de "ondas de materia" estacionarias en el condensado de Bose. Fuente .

^(*) Si el tamaño de las partículas vertidas en la placa es lo suficientemente pequeño, entonces serán expulsadas no a los nodos, sino a los antinodos de la onda estacionaria, como se mostró en este trabajo experimental .

^(**) «» «» , : – , , . .

^(***) – . , , , .

^(****) , – . , . – .