En el siglo XX, los expertos en física de partículas descubrieron que es muy importante tener en cuenta todas las simetrías posibles que pueden demostrar las leyes de la naturaleza que rigen las partículas elementales. La presencia o ausencia de simetría puede revelarnos aspectos de la naturaleza que de otro modo no serían obvios.
De las muchas simetrías posibles, tres pueden desempeñar un papel único:
conjugación de carga (C),
paridad espacial (P) y
simetría con respecto a la inversión de tiempo (T). Tres de estas transformaciones, que afectan a las partículas, el espacio y el tiempo, incluyen:
• C: reemplazar todas las partículas con partículas de carga opuesta (tanto una carga eléctrica como cargas menos familiares; incluso algunas partículas neutras se reemplazan. Por ejemplo, los neutrinos cambian a antineutrinos y los neutrones a antineutrones).
• P: colocando el mundo en un espejo (más precisamente, cambiando la orientación de tres dimensiones a la opuesta).
• T: lanzar el mundo en la dirección opuesta del tiempo (más precisamente, cambiar la dirección de la evolución temporal).
Cada una de estas transformaciones tiene la propiedad de que si la realiza dos veces, volverá al estado original. En jerga, decimos que P
2 = P × P = 1 (es decir, si pones un espejo en un espejo, lo que ves se verá igual que si no hubiera espejos), y, de manera similar, C
2 = 1 y T
2 = 1.
Además, puede realizar dos conversiones juntas. Por ejemplo, puede hacer C, y luego P, que simplemente escribimos como "CP" (o puede hacer PC, será lo mismo; el orden no importa para estas transformaciones), en el que pone el mundo en el espejo y cambia cargas de partículas Puede considerar CT, PT e incluso CPT. Además de C, P y T, cualquiera de estas combinaciones, cuando se hace dos veces, devolverá todo como estaba.
¿Y qué hacemos con estas transformaciones? Necesitamos hacer una pregunta: si imaginamos un mundo creado a partir del nuestro a través de una de las transformaciones, ¿las leyes de la naturaleza en él, que rigen las partículas e interacciones elementales, funcionarán de la misma manera que en el nuestro?
Si la respuesta es sí, entonces todo lo que puede suceder en un mundo nuevo y transformado puede suceder en el nuestro; En este caso decimos que esta transformación es la simetría de nuestro mundo. Más precisamente, esta es la simetría de las leyes de la naturaleza de nuestro mundo. Si no, entonces la transformación aún puede llevarse a cabo, pero no será la simetría de nuestro mundo, porque el mundo obtenido después de la transformación será diferente al nuestro.
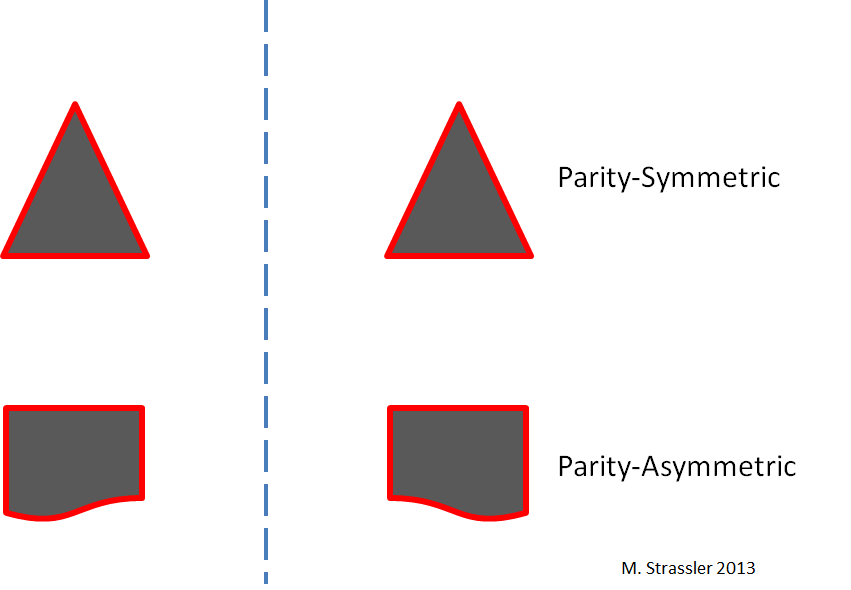Fig. 1Es bastante fácil entender cómo funciona la paridad espacial (P). Un objeto particular puede o no tener simetría de paridad. Como se muestra en la fig. 1, el reflejo de un triángulo en el espejo nos da un triángulo idéntico al primero, de modo que el triángulo será simétrico en paridad. Pero una forma más compleja, que se muestra en la parte inferior de la fig. 1, no se ve exactamente igual después de la reflexión, por lo tanto, es asimétrico en paridad.
Obviamente, nuestro mundo no es simétrico en el espejo; esto se puede ver en cualquier fotografía de la naturaleza (ver Fig. 2). Sin embargo, es necesario distinguir entre la simetría del objeto y la simetría de las leyes de la naturaleza que gobiernan todos los objetos posibles. Los procesos básicos de la física de partículas pueden ser simétricos, lo que significa que para cualquier proceso que pueda ocurrir en la naturaleza, también puede ocurrir un proceso espejo (Fig. 2, abajo).
¡Pero resulta que los procesos básicos de la naturaleza no son simétricos en P!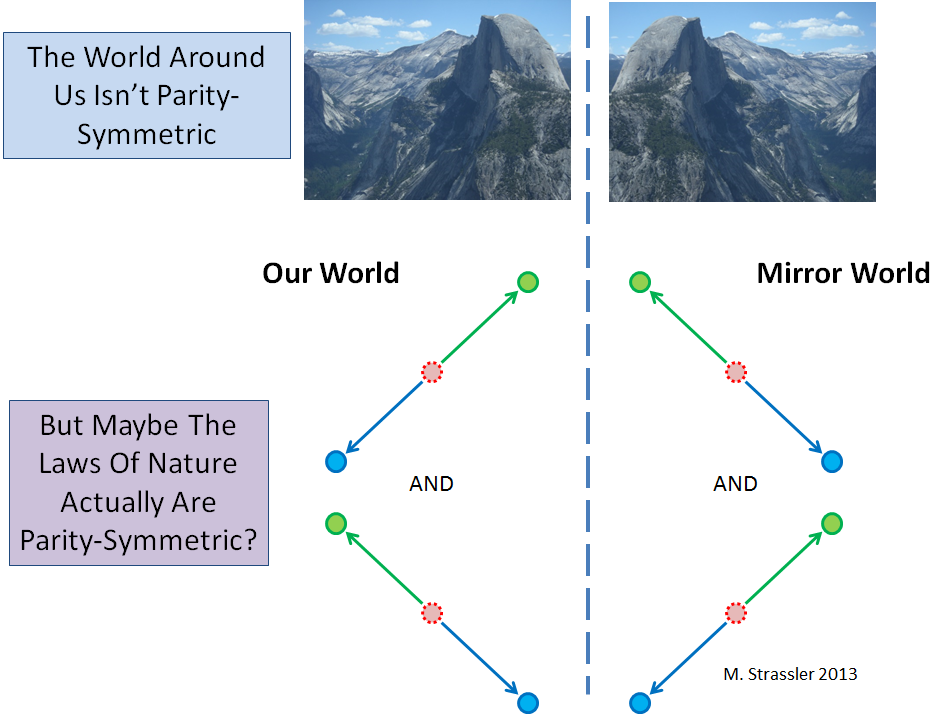
Fig. 2Un hecho sorprendente es que ni C, ni P, ni T, ni CP, ni CT, ni PC son simetrías de la naturaleza. Los principales procesos conocidos por la física antes del siglo XX, en particular, incluidas las interacciones gravitacionales y electromagnéticas, es decir, todos aquellos que mantienen unida a la Tierra y mantienen su órbita alrededor del Sol, y aquellos que controlan la física de los átomos y las moléculas y toda la química, son simétricos en S, P y T. Por lo tanto, los físicos se sorprendieron bastante cuando en las décadas de 1950 y 1960 descubrieron que la interacción nuclear débil rompe todas estas simetrías. La única transformación que todavía se considera (por una buena razón) simétrica a la naturaleza es la CPT.
Tenga en cuenta que si CPT es simetría, los efectos de CP y T deberían ser los mismos. Dado que esto es simetría, la aplicación de la transformación CPT lo lleva de regreso al mismo mundo desde el que comenzó, pero también se sabe que si aplica la transformación T dos veces, volverá al mismo mundo desde el que comenzó, lo que significa que CP debe hacerlo lo mismo que hace T. Lo mismo es cierto para los pares CT y P, y para RT y C.
La CPT transforma las partículas y sus interacciones en nuestro mundo en antipartículas y sus interacciones en un mundo transformado, y viceversa. Y, dado que en nuestro mundo, cada tipo de partícula tiene una antipartícula (sucede que en sí misma lo es), y dado que cada interacción de diferentes partículas tiene anti-interacción con antipartículas (por así decirlo), se cree que esto es perfectamente simétrico. Más precisamente, para cualquier mundo cuyas partículas obedecen a la teoría del campo cuántico, las matemáticas utilizadas en las ecuaciones del Modelo Estándar, que describe todas las partículas e interacciones conocidas, se puede demostrar que CPT es simetría. (Es esto cierto para una teoría unificadora, como la teoría de cuerdas, que combina la teoría cuántica de la gravedad con fuerzas no gravitacionales, es difícil de decir; pero las violaciones CPT aún no se han obtenido en experimentos).
C y P no son simetrías debido a la interacción nuclear débil
Hasta la década de 1950, todo lo que los físicos sabían, toda la química y la física atómica, todos los efectos de la gravedad y la interacción electromagnética, las ondas de luz y los cimientos del núcleo atómico, correspondía a un mundo simétrico en P. Pero resulta que C y P no son casi simetrías leyes de la naturaleza. Se ven perturbados con la mayor frecuencia posible por interacciones nucleares débiles.
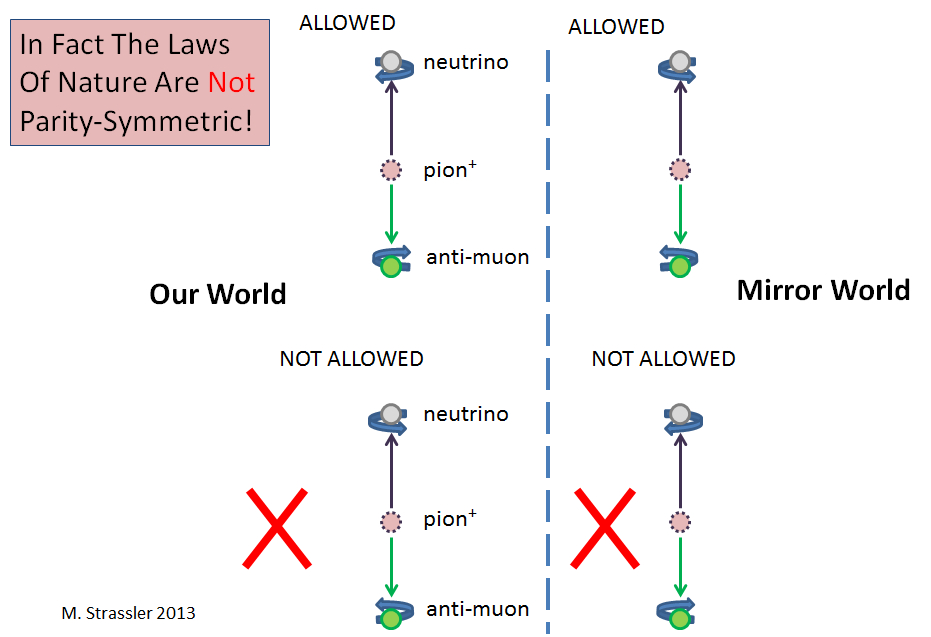Fig. 3En el ejemplo más simple (pero no el único), los neutrinos están involucrados. Cuando un neutrino aparece en un proceso físico, siempre se crea utilizando una interacción nuclear débil. Y cuando ocurre, siempre gira en sentido antihorario desde el punto de vista del observador ubicado en el punto de donde viene. (Los neutrinos, como los electrones y protones y muchas otras partículas, en cierto sentido siempre giran; más precisamente, siempre tienen un par). En otras palabras, gira como un tornillo zurdo (Fig. 3). (En jerga tendrá una helicidad negativa). Pero el neutrino producido por la débil interacción nuclear nunca gira como un tornillo diestro. Dado que P intercambiaría lugares diestros y zurdos (como en un espejo), esto significa que una interacción nuclear débil viola a R.
En un ejemplo más específico (Fig.3), cuando un pión con carga positiva (un hadron que consiste en un quark superior, un quark anti-bajo y muchos pares de gluones y quark / antiquark) se descompone en un antimuón y un neutrino, el neutrino siempre es zurdo y nunca diestro. Esto viola a R. Y cuando un pión con carga negativa se descompone en un muón y un antineutrino, el antineutrino siempre es diestro. Esta diferencia en los procesos, incluidas las peonías cargadas negativa y positivamente, viola C.
La violación de P y C de este tipo es ahora bastante comprensible. El modelo estándar (las ecuaciones que usamos para describir todas las partículas e interacciones conocidas) lo incluye de una manera bastante natural, y los detalles de las ecuaciones se verificaron cuidadosamente en los experimentos. Entonces, aunque las violaciones de P y C fueron una gran sorpresa en la década de 1950, hoy son una parte estándar de la física de partículas.
Sin embargo, si observamos las partículas mismas (y no entramos en los detalles de sus interacciones), SR (lo mismo que RS) a primera vista parece simétrico. Esto se debe a que P gira el giro del neutrino de izquierda a derecha, pero C invierte la carga del pión, convierte el antimuón en un muón y reemplaza el neutrino con un antineutrino; El proceso final tiene lugar en nuestro mundo (Fig. 4). Entonces, durante algún tiempo, los físicos creyeron que la interacción nuclear débil preservaría la SR, aunque individualmente viola tanto C como R.
Otra forma de ver esto es leer
mi artículo sobre cómo se verían las partículas si el campo de Higgs fuera cero. Se puede ver que, por ejemplo, las partículas izquierda de electrones y izquierda de neutrinos están emparejadas y están sujetas a la acción de interacción débil de isospin, y la partícula derecha de electrones está separada de la de neutrino-derecha, y ninguna de ellas está sujeta a interacción débil de isospin. Además, lo que es cierto para la partícula derecha de electrones también es cierto para la partícula derecha de positrones, y lo que es cierto para la partícula derecha de positrones es cierto para la izquierda de electrones. Pero P cambia las partículas electrón izquierda y derecha electrónica, así que obviamente esto no es simetría; C cambia el electrón a la izquierda y el positrón a la izquierda, y dado que la partícula izquierda del positrón no se ve afectada por la interacción débil, C tampoco es una simetría. Sin embargo, CP cambia las partículas electrón-izquierda y positrón-derecha, y ambas están sujetas a una interacción nuclear débil.
Fig. 4 4CP tampoco es simetría
Pero en la década de 1960, resultó que SR también está perturbado por una interacción nuclear débil. Esto nuevamente fue una sorpresa, comprensible hoy, pero aún siendo explorado por nosotros. Aquí hay una historia corta.
La mayoría de los hadrones (partículas que consisten en quarks, antiquarks y gluones) se descomponen casi instantáneamente a través de una fuerte interacción nuclear, por veces menos de una billonésima de billonésima de segundo. Un hadron, protón, es estable; el neutrón mismo vive 15 minutos. (Los núcleos atómicos que consisten en protones y neutrones también se denominan a menudo hadrones, pero personalmente prefiero llamarlos "conjuntos de hadrones"). Pero para varios hadrones de importancia histórica y práctica, la vida útil, aunque pequeña, no es muy buena (entre una billonésima parte de una billonésima de segundo a una billonésima de segundo) y la mayoría de ellos decaen debido a una interacción nuclear débil (otros decaimiento a través de la interacción electromagnética). Y en algunos de ellos, especialmente los mesones que contienen un quark inferior o un antiquark inferior, se midieron las desintegraciones que violan la SR. Otros signos de violación de CP están en las oscilaciones entre dos hadrones, similar a las oscilaciones de neutrinos.
Este tipo de violación de PC es muy interesante porque ocurre naturalmente donde hay tres o más aromas o generaciones de quarks superiores (superiores, encantados y verdaderos) y tres aromas de quarks inferiores (inferiores, extraños y encantadores). Como señalaron Kobayashi y Maskawa, en una versión del Modelo Estándar que contiene solo dos generaciones, no podría haber tal violación de SR; él debería tener una razón completamente diferente. Como observaron esto mucho antes que el descubrimiento de la tercera generación de partículas, de hecho, predijeron la necesidad de la existencia de la tercera generación, por lo que posteriormente se les otorgó el Premio Nobel de física en 2008 (junto con Nambu por su gran trabajo en otros campos).
Hasta ahora, no hay signos de violación de CP que tengan una naturaleza diferente a la de Kobayashi y Maskawa. Pero si hay partículas e interacciones distintas de las que conocemos en el Modelo estándar, puede haber otras condiciones en las que se viole la PC.
Sin embargo, incluso dentro del Modelo Estándar, hay un gran misterio.
Fuerte interacción nuclear y SR
Es muy inesperado que la interacción nuclear fuerte no perturbe significativamente la SR, y nadie sabe por qué es así. Sabemos que una interacción fuerte no viola mucho la superredes debido a una cierta propiedad del neutrón, conocida como el
momento dipolar eléctrico .
Un neutrón es un hadron eléctricamente neutro muy similar a un protón. Los quarks, antiquarks y gluones que forman el neutrón se mantienen unidos por una fuerte interacción nuclear. Se puede hacer una pregunta interesante sobre cualquier momento eléctricamente neutro: ¿tiene un dipolo eléctrico?
El imán con el que solías jugar de niño es un dipolo magnético que tiene un polo norte y un polo sur (Fig. 5). Un monopolo magnético sería el polo norte o sur; pero nunca has visto esto, y nadie lo ha visto. Un dipolo eléctrico tiene una carga eléctrica cero, pero por un lado tiene cargas positivas y, por otro, negativas. Este puede ser un caso tan simple como un átomo de hidrógeno, con un electrón en el papel de una carga negativa y un protón en el papel de uno positivo.
Para un dipolo eléctrico simple, que consta de dos cargas separadas por una distancia D, una de las cuales tiene una carga q, y la otra -q, el momento dipolar eléctrico simplemente se define como q × D. Tenga en cuenta que si la carga positiva y negativa se sientan en un lugar, entonces tal objeto no tiene un momento dipolar; las cargas deben estar separadas en el espacio para que se "polarice". El átomo de hidrógeno generalmente no está polarizado. Pero muchas moléculas tienen un momento dipolar, aunque son eléctricamente neutrales. Por ejemplo, una molécula de agua H
2 O tiene un momento dipolar de 3.9 × 10
-8 e cm, donde "e" es la carga de protones (e es la carga de electrones), y cm es 1 centímetro. A modo de comparación, esto es solo un poco menos de lo que se puede obtener al diluir el electrón y el protón a una distancia aproximadamente igual al tamaño de la molécula de agua (para tal dipolo, el momento dipolar sería del orden de 9 × 10
-8 e cm). Esto sugiere que los electrones de dos átomos de hidrógeno en H2O pasan mucho tiempo con el átomo de oxígeno.
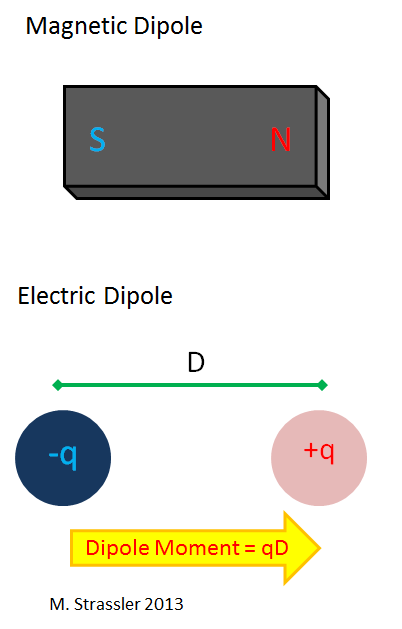Fig. 5 5¿Qué tan grande puede ser el momento dipolar de neutrones? El radio de neutrones es del orden de
10-13 cm, por lo que uno esperaría que D sea aproximadamente el mismo. Y se compone de quarks, antiquarks y gluones; los gluones son eléctricamente neutros, pero los quarks y antiquarks tienen cargas eléctricas: 2/3 e (quark superior), –1/3 e (quark inferior), –2/3 e (antiquark superior) y +1/3 e (antiquark inferior ) Entonces uno esperaría q sea algo como esto. Resulta que uno esperaría que la magnitud del momento dipolar eléctrico del neutrón fuera de
10-13 e cm. Esto es un millón de veces más pequeño que el momento dipolar de una molécula de agua, principalmente porque el radio de neutrones es menos de un millón de veces.
De hecho, algunos efectos no obvios nos dan una estimación de un tamaño aún más pequeño. La expectativa real está en la región de
10-15 e cm.
Pero si el neutrón tiene un momento dipolar eléctrico, esto violaría T, y por lo tanto CP, si CPT puede considerarse al menos una simetría aproximada (esto también viola P). Entonces, si CP y CPT fueran simetrías exactas, entonces el dipolo de neutrones eléctrico tendría que ser cero.
Por supuesto, ya sabemos que CP no es una simetría exacta; Está roto por una débil interacción nuclear. Pero la interacción débil es tan débil (al menos con respecto a los neutrones) que puede dar al neutrón un momento dipolar de electrones del orden de 10
-32 e cm. ¡Esto es mucho menos de lo que podemos medir! Entonces, para nuestros propósitos, puede considerarse cero.
Pero si la interacción fuerte que mantiene unido al neutrón viola la superredes, entonces esperamos que el momento dipolar eléctrico sea de
10-15 e cm. Sin embargo, ¡el experimento muestra que el momento dipolar eléctrico del neutrón es inferior a 3 ×
10-26 e cm! Esto es diez mil millones de veces menos de lo esperado. Por lo tanto, una interacción nuclear fuerte no viola la superredes tan fuertemente como se esperaba.
¿Por qué es tan menos de lo esperado? Nadie lo sabe, aunque ha habido muchas suposiciones. Este enigma se llama el
fuerte problema de PC y es uno de los tres mayores problemas que afectan a la física de partículas, junto con
el problema de la jerarquía y
el problema de la constante cosmológica .
Específicamente, el problema es el siguiente. Si escribe la teoría de la interacción nuclear fuerte (las ecuaciones para gluones, quarks y antiquarks, llamadas QCD), estas ecuaciones tendrán diferentes parámetros, a saber:
• La fuerza unificadora de una fuerte interacción nuclear,
• masas de diferentes quarks,
• ángulo theta, que no afecta a los diagramas de Feynman, pero que, sin embargo, determina los efectos de varios procesos sutiles (túnel cuántico,
instantones , pseudopartículas) de la física del gluón.
¿Detener qué? ¿Cuál es este último artículo? Bueno, este parámetro opcional QCD se descubrió en la década de 1970 (esta es una de las áreas en las que
Alexander Polyakov , quien recientemente ganó el premio, se hizo famoso). El problema en sí es de naturaleza demasiado técnica para ser descrito aquí, pero es suficiente decir que si el ángulo theta no es 0 o π, entonces una interacción nuclear fuerte viola la superredes. Más precisamente, CP viola una cierta combinación de ángulo theta y masas de varios quarks (específicamente, el producto de las fases complejas de sus masas). Y estos dos parámetros (ángulo theta y masas de quark) no tienen una conexión obvia, entonces, ¿cómo se combinan para compensarlos perfectamente? Sin embargo, por alguna razón, su combinación es cero, o al menos diez mil millones de veces más pequeña de lo que podría ser. No hay razones obvias para esto.
Se pueden dar las siguientes explicaciones a este acertijo, de casi 40 años:
• el quark superior puede no tener masa (esto es muy difícil de verificar, ya que no se puede medir directamente; los métodos indirectos han estado diciendo que su masa es varias veces la masa de un electrón, pero algunas sutilezas no nos permiten interpretar estos métodos con total certeza).
• Quizás haya un
campo axión que elimine este efecto; Esta idea predice la existencia de una partícula de axión, que se ha buscado durante más de 30 años, pero aún no se ha encontrado. , , .
, ; , , .