Entre los métodos numéricos utilizados en el proceso de diseño de componentes ópticos modernos, generalmente se distinguen dos grandes grupos: onda completa universal y aproximada. La elección de un enfoque específico depende de la relación del objeto simulado con la longitud de onda y la naturaleza de la propagación de las ondas electromagnéticas.

Los métodos de onda completa basados ​​en la solución directa de ecuaciones de onda para los componentes del campo electromagnético en condiciones de límite dadas generalmente se utilizan para desarrollar micro y nanodispositivos ópticos. Mientras que para el diseño de sistemas macroscópicos como lentes de enfoque, interferómetros y monocromadores, se utilizan métodos aproximados. Estos, en particular, incluyen el trazado geométrico de rayos.

En este artículo, además de un breve análisis de dos métodos tradicionales, hablaremos sobre un enfoque más nuevo llamado método de envoltura de haz y discutiremos sus ventajas para la óptica computacional.

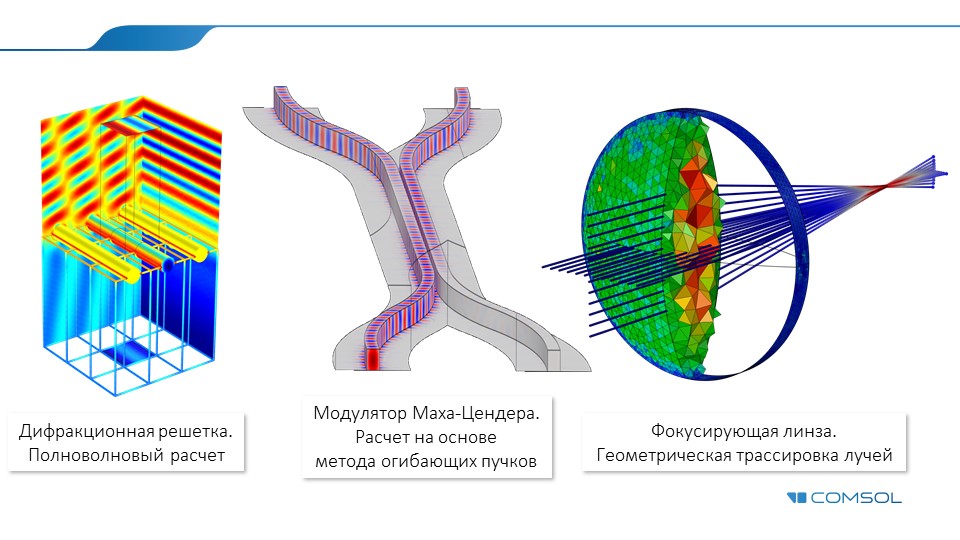
Métodos de onda completa

El primer grupo incluye el método espectral, el método de momentos, el método de diferencias finitas y el método de elementos finitos. Se han utilizado con éxito durante muchos años y hoy en día se utilizan activamente en el análisis de componentes ópticos tan importantes como estructuras de fibra óptica, acopladores direccionales, resonadores de anillo, etc. Utilizando estos métodos, los ingenieros e investigadores pueden realizar un análisis preciso de la propagación de ondas en estructuras ópticas utilizando un conjunto mínimo de supuestos físicos. Estos últimos están asociados con la discretización cuando se convierte un medio óptico continuo por partes en un modelo digital (discreto). Por lo tanto, los fenómenos de difracción, interferencia y modos de resonancia de bajo orden se pueden rastrear con una precisión casi arbitraria, simplemente aumentando el nivel de muestreo (Fig. 1), mientras que tales métodos generalmente se denominan onda completa (onda completa).

Fig.1. La incidencia de una onda electromagnética plana en una nanoesfera de oro: una imagen de un campo eléctrico disperso y una cuadrícula de elementos finitos calculada.

En general, para los métodos de diferencias finitas, aumentar el nivel de discretización se reduce a agregar puntos adicionales al dominio computacional y obtener una representación más uniforme del campo electromagnético. Un principio similar se aplica a otros métodos. Sin embargo, un mayor número de puntos de muestreo conduce a un aumento en los recursos computacionales necesarios para el cálculo. Para los modelos 3D, el número de tales puntos es proporcional a la longitud de onda en el cubo. Según el criterio de Nyquist, la longitud de onda debe tener al menos dos puntos de muestreo a lo largo de cada eje de coordenadas, y en condiciones reales, incluso más (generalmente al menos 5 elementos de segundo orden en cada dirección espacial). En la práctica, los costos de computación crecen aún más rápido, por lo tanto, para calcular objetos que se ajustan a una gran cantidad de longitudes de onda (más de 50), los métodos de onda completa rara vez se usan en ausencia de otras alternativas.

Un ejemplo simple: el ancho de una fibra óptica puede ser solo de unas pocas longitudes de onda, y su longitud es de varios miles de millones de longitudes de onda. Para analizar los modos de propagación en la sección transversal de la fibra, los métodos de onda completa son excelentes porque el tamaño relativo de la fibra en esta dirección es pequeño (Fig. 2). Por el contrario, para analizar la propagación de las ondas a lo largo de la fibra y los posibles defectos de la fibra, uno tiene que recurrir a métodos aproximados para no agotar la RAM de la computadora.

Fig. 2. Cálculo basado en el método de elementos finitos de la estructura de fibra óptica: red de elementos finitos (izquierda) y uno de los modos de fibra transversal a una longitud de onda de 1,2 μm (derecha).

Métodos aproximados

Los métodos aproximados implican el uso de algunas simplificaciones o aproximaciones iniciales. Esta clase de métodos incluye métodos como el trazado de rayos (u óptica geométrica ), la óptica gaussiana y el método de propagación del haz (BPM) . A diferencia del enfoque de onda completa, bajo ciertas condiciones, se pueden aplicar métodos aproximados para resolver problemas en objetos mucho más grandes.

Por ejemplo, decenas de miles de longitudes de onda de luz visible se ajustan a una lente con un diámetro de 1 cm en cualquier dirección. En este caso, el método para rastrear haces ópticos se muestra mejor. La recompensa por la aproximación es la negativa a tener en cuenta algunos fenómenos físicos: en óptica geométrica, la difracción generalmente se descuida: los rayos se propagan en línea recta (Fig. 3).

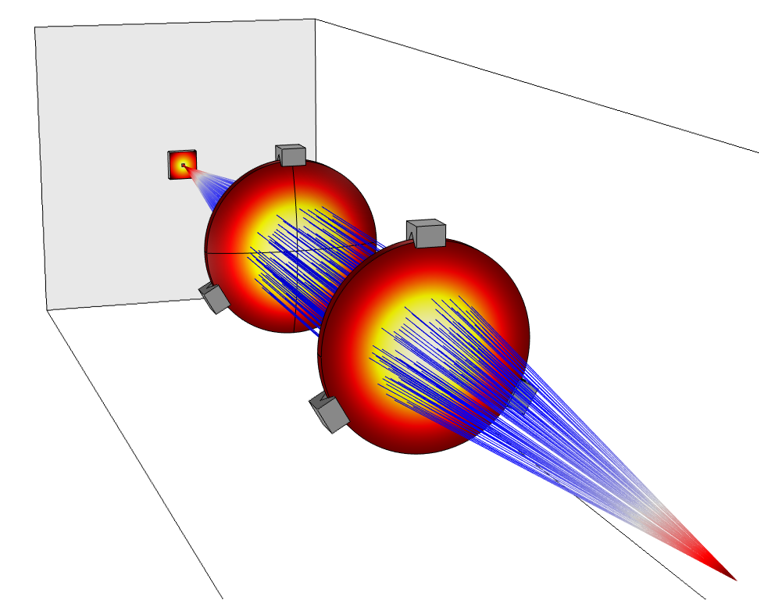
Fig. 3. Un análisis numérico de la propagación de ondas electromagnéticas en un sistema de enfoque de haz láser generalmente se basa en el trazado de rayos, en lugar de resolver directamente las ecuaciones de Maxwell mediante el método de onda completa.

Método de sobre de haz

Las guías de ondas en los sistemas ópticos generalmente tienen una dirección preferida de propagación de ondas. En el lenguaje de la física matemática, esto significa que hay un determinado vector de onda que varía ligeramente o incluso permanece constante en la dirección de propagación. Un nuevo método computacional se basa en esto: el método de envolvente de haz .

En el caso más general, el campo eléctrico de una onda de propagación contiene tres componentes: $$$E = (E_x, E_y, E_z)$. Suponga que el eje z es la dirección preferida de propagación, y que el campo dentro de la estructura de la guía de onda oscila significativamente a lo largo del eje z y contiene cambios mucho más lentos en las direcciones x e y . Entonces, el campo de una onda electromagnética continua con una frecuencia constante se puede representar como $$$E = E_1 (x, y, z) cos (wt-k_zz)$donde $$$w = 2 \ pi f$- frecuencia angular, $$$k_z$Es la propagación constante a lo largo del eje z , y $$$E_1$- Amplitud que cambia lentamente.

Esta expresión en forma compleja $$$E = E_1 \ exp (i (wt-k_zz))$puede sustituirse en el conjunto completo de ecuaciones de Maxwell y, utilizando una serie de transformaciones algebraicas clásicas, lograr la reducción de todos los factores que cambian rápidamente $$$\ exp (i (wt-k_zz))$, obteniendo la ecuación final para una envolvente de campo que varía relativamente lentamente $$$E_1$. Es en esta reducción exitosa del componente rápidamente variable en la que se basa el método de la envoltura del haz . Para volver a la verdadera expresión de una onda electromagnética, solo necesita multiplicar la expresión resultante por este factor.

Debido a la falta de aproximaciones (la única suposición se refiere a la dirección inicialmente conocida de propagación de ondas), este enfoque puede clasificarse como un método de onda completa (Fig. 4), pero tiene una ventaja importante. El problema con los métodos de onda completa es que requieren una cantidad suficiente de puntos de diseño o nodos en la muestra, porque De lo contrario, los resultados del cálculo serán solo una "basura" numérica. Para resolver la ecuación para una envolvente de campo que varía relativamente lentamente, es suficiente un número mucho menor de puntos nodales (manteniendo la validez del criterio de Nyquist), al menos en los casos en que el problema tiene una dirección de propagación claramente definida, como en las guías de ondas ópticas (Fig. 4 ) Por lo tanto, el número requerido de puntos de muestreo o nodos puede reducirse en un orden de magnitud (en algunos casos, incluso más). Es importante tener en cuenta que se puede usar cualquier método universal para calcular la envoltura del haz, en particular, el FEM, y luego para obtener una solución completa, es suficiente simplemente multiplicar la envoltura por el componente rápidamente cambiante conocido (inicialmente dado).

Este enfoque difiere significativamente de un método de nombre similar: el método de propagación del haz, que utiliza simplificaciones y aproximaciones adicionales, descuidando algunas derivadas en la ecuación de onda.

Fig. 4. Comparación de la discretización del método tradicional de onda completa y el método de envolvente de haz.

Método de envoltura de haz y dirección de propagación de onda

La capacidad de calcular estructuras largas y delgadas con una dirección de propagación de onda más o menos constante es muy útil, y aplicar el método de envoltura de haz a tales casos es bastante simple. Sin embargo, muchas estructuras de guía de onda están curvadas en una o más direcciones. El método propuesto también funcionará en este caso, pero existen algunas limitaciones asociadas con la complejidad geométrica del diseño. Si el vector de propagación cambia lentamente de dirección, el método sigue siendo válido. Para comprender lo que sucede en este caso, volvamos a la expresión completa del campo electromagnético. $$$E = E_1 \ exp (i (wt-k_zz))$, donde la dirección de propagación se da inicialmente a lo largo del eje z . Para generalizar esta expresión al caso de una dirección arbitraria, la escribimos en la forma $$$E = E_1 \ exp (i (wt-k * r))$donde $$$k = (k_x, k_y, k_z)$- un vector que determina la dirección preferida de propagación de onda, y $$$r = (x, y, z)$Es el vector de coordenadas $$$k * r$- su producto escalar.

En la práctica, este último generalmente se establece igual a la función de fase distribuida espacialmente $$$\ phi (x, y, z) = k * r = k_xx + k_yy + k_zz$. Luego, desde el punto de vista del método de envoltura del haz, la condición de la dirección de propagación que cambia lentamente se reemplaza por la condición de la fase de cambio lento. Por ejemplo, la parte anular de un resonador de radio R puede describirse mediante la función de fase $$$\ phi = Rk_p \ arctan (y / x)$donde $$$k_p = 2 \ pi / \ lambda_p$- constante de propagación correspondiente a la longitud de onda $$$\ lambda_p$en la dirección de propagación (Fig. 6).

Fig. 6. Análisis del resonador de anillo a una longitud de onda de 1,559 micras. La cuadrícula de elementos finitos se muestra a la izquierda, un campo físico que varía rápidamente en el centro y una envolvente de campo que varía lentamente calculada utilizando el método de envoltura de haz a la derecha.

Por lo tanto, el método de envoltura del haz se puede aplicar a estructuras ópticas compuestas de formas simples, donde cada componente componente se puede describir a través de una función $$$\ phi (x, y, z)$correspondiente a la dirección de distribución local preferida. Por ejemplo, un resonador de anillo que contiene una sección directa y una sección de anillo puede investigarse usando una función de fase constante y una "circular". En un caso más general, la función de fase se puede definir como la interpolación de una cierta dependencia simple del vector de coordenadas. Además, utilizando el principio de superposición de campos, es posible analizar dos (ondas directas y hacia atrás) y más direcciones de propagación (incluidos problemas de reflexión y refracción), registrando varios conjuntos de funciones de fase (Fig. 7).

Fig. 7. Distribución de una envoltura de campo que varía lentamente en una cavidad láser simétrica . En el cálculo se utiliza una superposición de ondas (hacia adelante y hacia atrás) que se propagan en dos direcciones.

Aplicación del método de envoltura de haz en óptica no lineal

Los efectos ópticos no lineales a menudo son bastante débiles y surgen a grandes longitudes de interacción, y en tales casos el método de envoltura de haz es el más adecuado. Un ejemplo de efectos no lineales es el autoenfoque. Este fenómeno puede observarse en barras láser o anteojos ópticos ubicados en el punto focal (por ejemplo, Nd: YAG - granate de itrio-aluminio dopado con neodimio). Conocer los valores umbral de autoenfoque en la etapa de diseño evitará daños a los materiales utilizados en la construcción de varios elementos (Fig. 8).

Fig. 8. Un estudio numérico del autoenfoque en una varilla BK-7 de 20 cm de largo , es decir. alrededor de 300 mil (!!!) longitudes de onda. La imagen a la derecha es la verdadera relación de aspecto, a la izquierda es la visualización a escala de la norma y el componente z de la envolvente de campo.

El método también es aplicable a otros efectos no lineales: generación de segundo armónico, generación de frecuencia total y diferencia, generación y amplificación paramétrica, así como la automodulación de fase.

Conclusión

El método de envoltura de haz puede aumentar significativamente el tamaño de los modelos a los que se aplican los métodos de onda completa. Llena la brecha entre los recursos informáticos exigentes, pero los esquemas precisos de diferencias finitas y elementos finitos y las técnicas de trazado rápido de rayos. El enfoque es aplicable para problemas de diseño reales, lo que confirma la solución exitosa de problemas aplicados, tanto desde el campo de la óptica no lineal como desde declaraciones interdisciplinarias, por ejemplo, calculando moduladores de Mach-Zehnder .

Los desarrolladores del método y su implementación en COMSOL esperan que su combinación con los métodos tradicionales de onda completa y aproximación abrirá nuevos horizontes en óptica y electrodinámica computacional para un estudio integral de procesos e / m en varias escalas espaciales.

PS Información adicional

Este artículo está basado en materiales de Optik & Photonik .

Para conocer más detalladamente los métodos descritos, lo invitamos a participar en nuestro nuevo seminario web "Cálculos de onda completa de componentes ópticos extendidos en COMSOL Multiphysics ^® " , que se realizará el 29 de noviembre de 2017.