 UPD: gráfico de función agregado.
UPD: gráfico de función agregado.Al igual que su creador Karl Weierstrass, este monstruo vino de la nada. Después de pasar cuatro años estudiando en la universidad para beber y hacer esgrima, Weierstrass se graduó con las manos vacías. Al final, comenzó a enseñar y la mayor parte de la década de 1850 fue maestro de escuela en Brownsburg. Estaba disgustado con la vida en un pequeño pueblo prusiano, encontró su existencia allí solo. La única salida para él eran los problemas matemáticos en los que trabajaba entre clases. Pero no tenía a nadie con quien hablar de matemáticas, y no tenía una biblioteca técnica para el entrenamiento. Incluso los resultados de su trabajo no pudieron salir de los límites de Braunberg. En lugar de publicar en revistas académicas, como haría un investigador universitario, Weierstrass las agregó a las avenidas escolares, asustando a los estudiantes potenciales con ecuaciones abstrusas.
Al final, Weierstrass envió uno de sus artículos a la estimada
revista Crele . A pesar de que los artículos anteriores apenas se notaron, esto causó un gran interés. Weierstrass descubrió una forma de trabajar con la terrible clase de ecuaciones conocidas como "funciones abelianas". En el artículo se dio un breve resumen de sus métodos, pero esto fue suficiente para convencer a los matemáticos del talento único del autor. No había pasado ni un año antes de que la Universidad de Konigsberg le otorgara a Weierstrass un doctorado honorario, y poco después, la Universidad de Berlín le ofreció el puesto de profesor. A pesar de que Weierstrass hizo un análogo intelectual del camino "de los harapos a las riquezas", muchos de sus viejos hábitos permanecieron. Raramente publicaba artículos, y prefería compartir su trabajo con los estudiantes. Pero no fue respetuoso no solo por el proceso de publicación: las "vacas sagradas" de las matemáticas no lo asustaron.
Weierstrass pronto comenzó a estudiar el trabajo de Augustin Louis Cauchy, uno de los matemáticos más destacados del siglo. Muchas de las obras de Cauchy han investigado análisis matemáticos y tasas de cambio (o "derivados"). Creó los conceptos básicos del diccionario de análisis matemático, identificando los conceptos más importantes de este tema. Pero cuando Weierstrass vio sus definiciones, las encontró detalladas y vagas. Tenían demasiados "gestos con las manos" y pocos detalles.
Decidió revisar el vocabulario de Cauchy, reemplazando la prosa con condiciones lógicas. El objetivo principal en sus primeros trabajos fue redefinir la derivada. Para calcular el gradiente de una curva en un punto y, por lo tanto, la velocidad de su cambio, Isaac Newton consideró inicialmente una línea que pasa por este punto y el punto vecino de la curva. Luego movió este punto vecino cada vez más cerca, hasta que la pendiente de la curva se volvió igual al gradiente de la curva. Pero este concepto fue difícil de definir matemáticamente. ¿Qué indica la "proximidad" de dos puntos entre sí?
De acuerdo con la definición detallada de Cauchy, el gradiente "se aproxima infinitamente a un valor fijo, de tal manera que, como resultado, difiere de él tanto como se requiere". Weierstrass no pensó que tal descripción sea lo suficientemente clara. Quería crear una definición más práctica, por lo que decidió convertir el concepto en una fórmula. En lugar de manipular ideas abstractas, los matemáticos deberían poder cambiar las ecuaciones. Trabajando en esto, sentó las bases de su monstruo.
En esa época, los matemáticos se inspiraron en gran medida en la naturaleza. Cuando Newton desarrolló el análisis matemático, se inspiró principalmente en el mundo físico: las trayectorias de los planetas, las oscilaciones del péndulo, el movimiento del fruto que cae. Tal pensamiento condujo al surgimiento de la intuición geométrica con respecto a las estructuras matemáticas. Deben tener el mismo significado que un objeto físico. Como resultado de esto, muchos matemáticos se han centrado en el estudio de funciones "continuas". Se pueden percibir como funciones que se pueden dibujar sin arrancar el lápiz del papel. Ponga la velocidad de la manzana que cae en el gráfico frente al tiempo y se convertirá en una línea continua, en la que no habrá saltos ni saltos bruscos. Se pensaba que la función continua era "natural".
En la opinión generalmente aceptada en ese momento, se podría encontrar un gradiente para cualquier número finito de puntos en cualquier curva continua. Esto parecía encajar intuitivamente: una línea puede tener varias piezas irregulares, pero siempre hay varias partes que son "suaves". El físico y matemático francés Andre-Marie Ampère incluso publicó una prueba de esta afirmación. Su argumento se basó en el hecho "intuitivamente obvio" de que una curva continua tiene partes en las que aumenta, disminuye o permanece plana. Esto significaba que se podía calcular un gradiente para estas áreas. Ampere no pensó en lo que sucedería cuando estas partes se volvieran infinitamente pequeñas, pero afirmó que esto no era necesario. Su enfoque fue lo suficientemente general como para evitar considerar los elementos "
infiniment petits " (infinitesimal). Para la mayoría de los matemáticos, esta lógica fue suficiente: a mediados del siglo XIX, casi todos los libros de texto sobre análisis matemático citaban la prueba de Ampère.
Pero en la década de 1860, aparecieron rumores sobre una criatura extraña, una función matemática que contradecía el teorema de Ampère. En Alemania, el gran Bernhard Riemann dijo a sus alumnos que conocía una función continua que no tiene partes lisas, y para la cual es imposible calcular la derivada de una función en ningún momento. Riemann no publicó pruebas, al igual que Charles Cellerier de la Universidad de Ginebra, quien escribió que había encontrado algo "muy importante y, me parece nuevo", pero ocultó su trabajo en una carpeta que se hizo pública solo después de su muerte durante varias décadas. despues Sin embargo, si se creyeran sus declaraciones, esto amenazaría los fundamentos mismos del incipiente análisis matemático. Esta criatura amenazó con destruir la feliz amistad entre la teoría matemática y las observaciones físicas en las que se basaba. El matanálisis siempre ha sido el lenguaje de los planetas y las estrellas, pero ¿cómo puede la naturaleza ser una fuente confiable de inspiración si hay funciones matemáticas que contradicen su esencia básica?
El monstruo finalmente nació en 1872 cuando Karl Weierstrass anunció que había encontrado una función continua, pero no uniforme en todos los puntos. Lo creó agregando una serie infinitamente larga de funciones coseno:
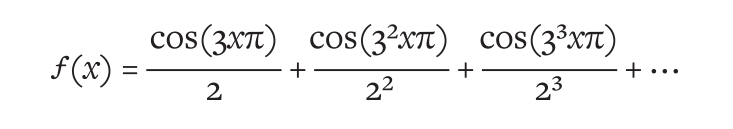
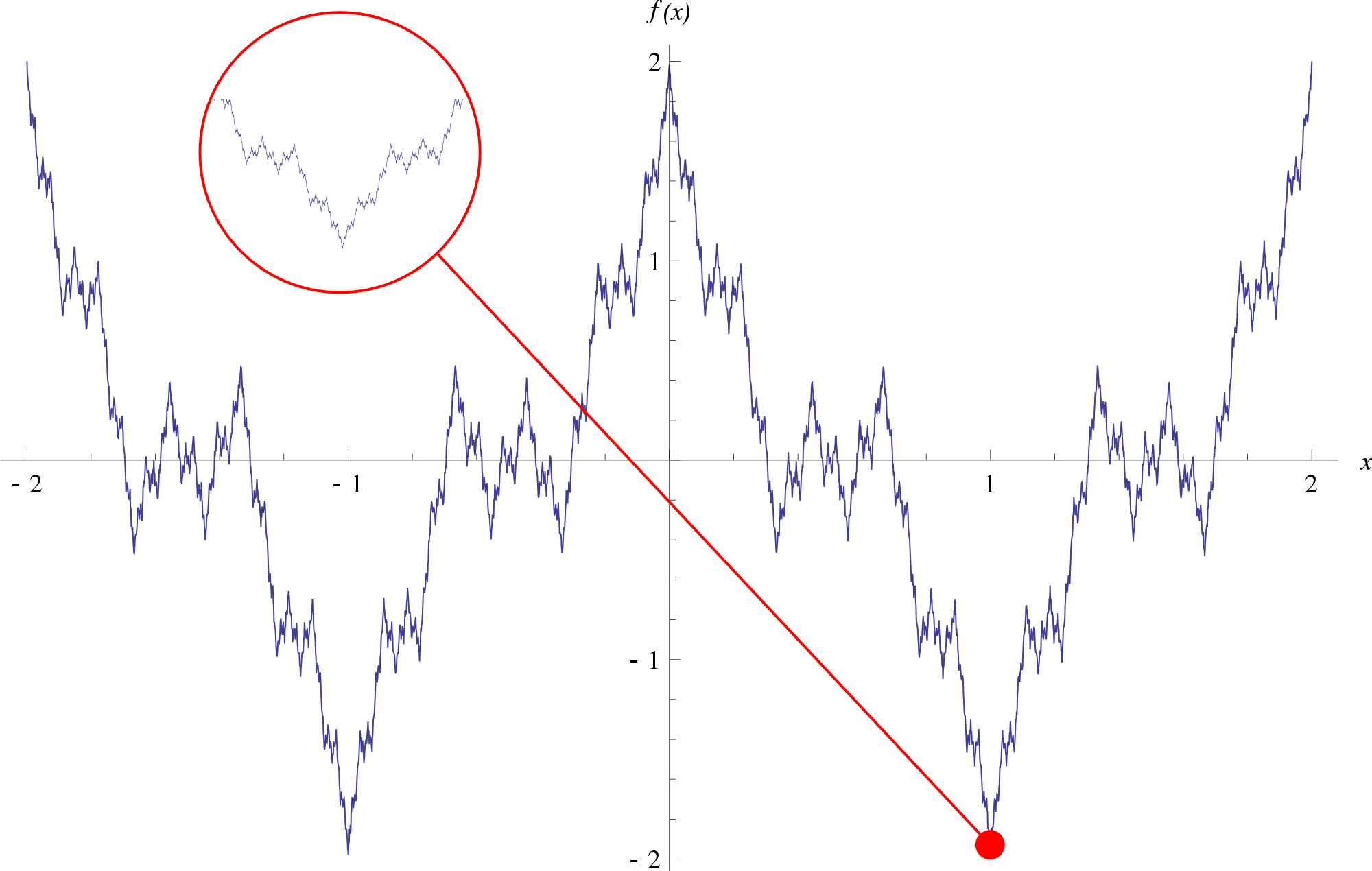
Como función, ella era fea y asquerosa. Ni siquiera estaba claro cómo se vería en el gráfico. Pero a Weierstrass no le importaba. Su prueba no consistía en formas, sino en ecuaciones, y esto fue lo que hizo que su declaración fuera tan poderosa. No solo creó un monstruo, sino que también lo construyó sobre una lógica de hierro. Tomó su propia definición rigurosa de la derivada y demostró que era imposible calcularla para esta nueva función.
El resultado llevó a la comunidad matemática a un estado de shock. El matemático francés Emil Picard dijo que si Newton supiera sobre tales funciones, no habría creado un análisis matemático. En lugar de albergar ideas sobre la física de la naturaleza, estaría atrapado en los intentos de atravesar barreras matemáticas difíciles. El monstruo comenzó a aflojar estudios anteriores. Los resultados, que parecían "probados", se estaban rompiendo en las costuras. Ampere usó las largas definiciones de Cauchy para probar su teorema de suavidad. Ahora su evidencia comenzaba a desmoronarse. Las vagas nociones del pasado eran impotentes contra el monstruo. Peor aún fue que ahora no se hizo evidente en qué consiste la prueba matemática. Los argumentos geométricos intuitivos de los últimos dos siglos se han vuelto inútiles. Cuando los matemáticos intentaron ahuyentar al monstruo, se mantuvo firme. Weierstrass demostró con una extraña ecuación que la intuición física no era una base confiable para construir teorías matemáticas.
Los matemáticos autorizados trataron de ignorar el resultado, argumentando que es feo e innecesario. Temían que los ratones de biblioteca y los alborotadores pudieran traer el caos a su campo de conocimiento favorito. En la Sorbona, Charles Hermite escribió: "Con disgusto y horror, me alejo de la lamentable inmundicia de las funciones que no tienen derivadas". Henri Poincaré, por primera vez llamando monstruos a tales funciones, calificó el trabajo de Weierstrass como "un insulto al sentido común". Argumentó que tales funciones son una distracción descarada de la esencia del sujeto.
"Fueron inventados para mostrar la falacia de los argumentos de nuestros predecesores", dijo. "Y además de esto, no podemos tomar ninguno de ellos".
Muchos de la "vieja guardia" querían dejar al monstruo de Weierstrass en el patio de las matemáticas. También fue inquietante que nadie pudiera imaginar la forma del animal que conocieron, solo después de la invención de las computadoras fue posible crear un gráfico de él. Su forma incomprensible evitó que la comunidad matemática entendiera cómo tal función podría existir. Además, el estilo de la prueba de Weierstrass era desconocido para muchos matemáticos. Su prueba contenía docenas de pasos lógicos y se extendió por varias páginas. La línea de razonamiento era apenas perceptible y requería un conocimiento técnico serio, pero en el mundo real no había análogos que ayudaran a comprender. Instinto instó a evitar esta evidencia.

Pero los monstruos tienen la costumbre de hacer su propio camino. De hecho, muchos de los conceptos que parecen obvios hoy, incluso necesarios, alguna vez fueron monstruos. Durante siglos, los matemáticos han rechazado los números negativos. Los antiguos griegos, que trabajaban principalmente con geometría, no vieron la necesidad de ellos. Lo mismo es cierto para los académicos medievales que adoptaron las ideas de los griegos. La sombra de este monstruo a veces parpadea incluso hoy, por ejemplo, en las preguntas de un niño que pregunta por qué, al multiplicar dos números negativos, resulta positivo. Pero en general, domesticamos a esta bestia: nadie quiere expulsarlo de nuevo.
Lo mismo sucedió con el monstruo de Weierstrass: comenzó a recibir un llamado. En 1904, Albert Einstein introdujo a los físicos a la idea del "movimiento browniano": dijo que las partículas en un líquido siguen caminos aleatorios porque las moléculas líquidas las repelen constantemente. Las colisiones son tan frecuentes (mayores de 10
21 por segundo) que no importa cuán bueno sea el microscopio o la observación cuidadosa, las trayectorias nunca serán suaves. Desde un punto de vista práctico, es imposible para ellos encontrar una derivada. Si los investigadores quieren trabajar con tales tareas, tendrán que enfrentarse al monstruo de Weierstrass. Eso es exactamente lo que hizo Einstein. Su teoría era que en el movimiento browniano se usaban funciones infinitamente rotas. Esto se ha convertido en un precedente importante: desde entonces, los físicos han utilizado funciones no suaves como una aproximación al movimiento browniano.
Cuando se hizo evidente que las llamadas "funciones de Weierstrass" eran realmente bastante útiles, los científicos comenzaron a desarrollar formas de trabajar elegantemente con funciones no suaves. En lugar de analizar el camino de una partícula individual en un líquido, comenzaron a considerar el comportamiento promedio de muchas partículas. ¿Qué tan lejos pueden viajar? ¿Cuándo pueden llegar a un punto dado? Fuera del campo de estudio del movimiento browniano, los matemáticos también comenzaron a repensar las herramientas básicas del matanálisis. La tasa de cambio siempre se determinó en relación con las distancias, y el área bajo la curva se midió geométricamente. Pero cuando las funciones no eran suaves, tales ideas no tenían sentido.
Kiyoshi Ito de la Universidad de Tokio descubrió una forma de evitar un problema al abordarlo en términos de probabilidades. Era una táctica poco ortodoxa, si no arriesgada: en la década de 1940, casi nadie consideraba que la teoría de la probabilidad fuera un área seria. Sin embargo, Ito insistió por su cuenta. Abordó las funciones como procesos aleatorios y tradujo las definiciones de Weierstrass a un nuevo lenguaje basado en probabilidades. Afirmó que dos procesos aleatorios son "cercanos" entre sí si sus resultados esperados son los mismos. Introdujo un método para trabajar con una función matemática, dependiendo de la cantidad de no suavidad, como en el movimiento browniano, en lugar de una variable más tradicional, por ejemplo, la distancia. Usando sus nuevos métodos, obtuvo un "Ito lemma" para calcular el cambio en una función de este tipo a lo largo del tiempo.
En la década de 1970, su trabajo se había convertido en un campo matemático completamente nuevo llamado cálculo estocástico (a los matemáticos les gusta llamar "estocástico" todo lo relacionado con la aleatoriedad). Como en el análisis en sí, apareció un conjunto completamente nuevo de herramientas y teoremas. Hoy en día, el cálculo estocástico se utiliza para estudiar todo tipo de fenómenos, desde las neuronas que trabajan en el cerebro hasta la propagación de enfermedades en una población. También se ha convertido en la base de las matemáticas financieras, en las que ayuda a los bancos a medir el valor de las opciones. Puede tener en cuenta el comportamiento desigual del tipo de cambio, lo que significa que muestra cuánto cambia el valor de la opción con el tiempo. La ecuación resultante, que se conoce como la fórmula Black-Scholes, ahora se usa en todos los pisos comerciales del mundo. Sin embargo, Ito siempre se ha sentido avergonzado por los elogios de los banqueros. Era un matemático teórico y no esperaba que su trabajo se conociera a través de la aplicación práctica.
El monstruo de Weierstrass sacudió los principios de la geometría. A finales del siglo XIX, el matemático sueco Helge von Koch se interesó en la idea de las funciones no suaves, pero quería estudiar su forma. Se dedicó a crear una forma (en lugar de una función) que no será uniforme en ninguna parte, lo que demuestra que los mismos monstruos se esconden en álgebra con geometría. Aunque no podía dibujar la función de Weierstrass, logró capturar a su pariente cercano. Trabajando en esta tarea en el proceso de búsqueda constante de trabajos temporales como profesor en prácticas, von Koch descubrió su existencia en 1904. Tomó un triángulo equilátero, luego agregó tres triángulos más pequeños a cada lado, y así hasta el infinito. La forma geométrica resultante era continua, pero no tenía derivadas. Debido a su aspecto sobresaliente, la figura rápidamente se hizo conocida como el "copo de nieve Koch".
Koch logró expandir el poder del monstruo de Weierstrass más allá del mundo de las ecuaciones y funciones. Pero como resultado de su trabajo, había algo más que merecía atención. En una inspección más cercana, resultó que su copo de nieve tenía una curiosa autosimilitud: agrandar una parte del copo de nieve, y se verá como una figura más grande. Muchos años después, se hizo evidente que la función Weierstrass tiene la misma propiedad.
Con el tiempo, tal auto-similitud comenzó a manifestarse en todo tipo de fenómenos. Para popularizar la idea de los objetos "fractales" en la década de 1980, se requirió el trabajo fundamental de Benoit Mandelbrot. Tales objetos tienen formas que se repiten en una escala cada vez más pequeña. Costas, nubes, plantas, vasos sanguíneos: los matemáticos han descubierto que los fractales son ubicuos en la naturaleza. Al igual que el copo de nieve de Koch, ninguno de ellos era liso. ¿Y qué tan suaves serían? Si la figura tiene partes lisas, el patrón desaparecerá con suficiente aumento. Como descubrió Koch, la forma más fácil de obtener una figura no lisa es crear un objeto fractal. Quizás el trabajo de Weierstrass inevitablemente lleve a los matemáticos al estudio de patrones similares, introduciendo a los investigadores al mundo de las estructuras hermosas y exquisitas.
El monstruo de Weierstrass continúa su trabajo hasta el día de hoy. Las ecuaciones de Navier-Stokes describen el movimiento de fluidos y subyacen a la dinámica de fluidos y la aerodinámica modernas que controlan todo, desde el diseño de la aeronave hasta el pronóstico del tiempo. Sin embargo, a pesar del hecho de que se crearon por primera vez en la década de 1840, los matemáticos aún no saben si siempre se pueden resolver. En 2000, el Clay Institute of Mathematics ofreció un bono de $ 1 millón a cualquiera que pudiera probar que estas ecuaciones siempre tienen soluciones suaves, o encontrar un ejemplo de lo contrario. Este problema se considera uno de los seis problemas pendientes más importantes en matemáticas, porque a pesar del uso generalizado de las ecuaciones de Navier-Stokes, los matemáticos no saben si estas ecuaciones siempre dan resultados físicamente confiables. El premio de 1 millón de dólares aún no es reclamado por nadie. En muchos sentidos, esto es un pago por la cabeza, provocando que los matemáticos busquen monstruos peligrosos.
En varios campos: desde la dinámica de fluidos hasta el sector financiero, criaturas como las funciones de Weierstrass han puesto en duda nuestras opiniones sobre la relación entre las matemáticas y el mundo natural. Los matemáticos que vivieron en los tiempos de Weierstrass creían que las matemáticas más útiles estaban inspiradas en la naturaleza y que el trabajo de Weierstrass no encajaba en esta definición. Pero el cálculo estocástico y los fractales de Mandelbrot demostraron que estaban equivocados. Resultó que en el mundo real, en un mundo real caótico y complejo, los monstruos se esconden en todas partes. Como dijo Mandelbrot, "la naturaleza bromeó con los matemáticos". Incluso el propio Weierstrass fue víctima de este truco.
Creó su función para objetar que las matemáticas deberían basarse solo en observaciones físicas. Sus seguidores creían que Newton estaba limitado por una percepción intuitiva del mundo real, y ahora, libres de estas limitaciones, podían descubrir nuevas teorías más universales y elegantes. Pensaban que las matemáticas ya no necesitarían la naturaleza. Pero el monstruo de Weierstrass demostró que todo es todo lo contrario. La conexión entre las matemáticas y la naturaleza es mucho más profunda de lo que cualquiera podría imaginar.Sobre el autor: Adam Kucharski es investigador en la Escuela de Higiene y Medicina Tropical de Londres, especializado en epidemiología matemática.