¿Puede existir un planeta toroidal?

Después de la publicación de mi artículo sobre lo que sería la Tierra, si fuera el doble de grande, los lectores tenían la pregunta: "¿Qué pasa con la Tierra toroidal"? La pregunta no es la más original, este tema ya se ha discutido en línea y su modelado se ha llevado a cabo. Pero me gusta hacer todo yo mismo, así que intenté realizar mi propio análisis.

¿Puede existir un planeta toroidal?

La estabilidad de un planeta toroidal no es obvia. Desde un punto de vista práctico, los planetas pueden considerarse bolas líquidas sin tensión superficial: la fuerza de una piedra no se puede comparar con el peso de un planeta. Poseen superficies gravitacionales equipotenciales teniendo en cuenta el potencial centrífugo. Si esto no fuera así, entonces habría lugares en ellos que podrían reducir su energía al fluir hacia un potencial más bajo. Otro hecho obvio es la existencia del límite superior de la velocidad de rotación, después de lo cual el planeta se desmoronará: la fuerza centrífuga en el ecuador excede la gravedad y el material vuela al espacio.

Se analizaron exhaustivamente las formas de equilibrio de los planetas elipsoidales rotativos sostenidos por la fuerza de su propia gravedad. Todo comenzó con Newton, luego se llevaron a cabo expediciones heroicas tempranas para establecer la forma de la Tierra, Maclaurin continuó su trabajo, Jacobi descubrió que a altas velocidades de rotación, los elipsoides con ejes desiguales son más estables que los elipsoides Macloren aplanados. Subramanyan Chandrasekar lideró desarrollos interesantes en esta área. Pero desde entonces han aparecido las computadoras y, por lo tanto, se han realizado cálculos analíticos y numéricos de casos más complejos o relativistas .

Del mismo modo, se analizaron las formas de equilibrio de los toroides rotativos; esto fue realizado por Poincare , Sophia Kovalevskaya y Frank Dyson ( Dyson 1893 , Dyson 1893b ). Al menos en teoría, es posible desenrollar un planeta elipsoidal a un estado de anillo, aunque hay muchas posibilidades de que ocurran oscilaciones que desestabilicen el sistema, después de lo cual se produce un salto al estado de anillo.

El anillo puede ser inestable, en particular, debido a la inestabilidad "nodal": se puede acumular una cantidad creciente de masa en ciertos meridianos, como resultado de lo cual habrá una brecha en varias masas separadas. Dyson analizó este caso y descubrió que es importante cuando R (la distancia desde el centro del toro hasta el centro de la tubería) excede de r (el radio de la tubería) más de tres veces, es decir, los aros delgados resultan inestables. También hay una velocidad de rotación más baja a la que el anillo se vuelve inestable y las fuerzas de marea lo comprimen en un elipsoide . Por lo tanto, la masa total y el momento angular deben establecerse correctamente desde el principio.

Aparentemente, las leyes de la física no prohíben la aparición de planetas toroidales. Solo la probabilidad de que ocurra es extremadamente pequeña, y es probable que dicho planeta sea inestable en las escalas de tiempo geológico debido a perturbaciones externas. Entonces, si suponemos que ya existe, posiblemente debido a las acciones de una civilización avanzada cuya estética es más fuerte que la mente, ¿cuáles serán sus propiedades?

Direcciones

Llamaremos dos círculos paralelos al plano de los ecuadores de rotación (externo e interno). En el caso de que no haya una diferencia fundamental entre ellos para el tema en discusión, los llamaré simplemente el ecuador. Los polos serán los círculos más alejados del plano ecuatorial.

La dirección al centro indicará la dirección al eje de rotación, al borde, desde el eje de rotación. Al plano: hacia el plano ecuatorial. Norte - hacia la parte más cercana del Círculo del Polo Norte, sur - hacia la parte más cercana del Círculo del Polo Sur.

Gravedad toroidal

¿Cómo funciona la gravedad en un planeta toroidal?

En el caso de R muy grande, el planeta toroidal se vuelve esencialmente cilíndrico. En este caso, la gravedad disminuye como 1 / r, donde r es la distancia desde el eje. El efecto en cualquier sección será proporcional a la masa total (proporcional a R) y la gravedad (proporcional a 1 / R), de modo que la fuerza total permanecerá constante al aumentar R. Equilibrará una cierta rotación. Gravedad superficial 2G rho / r, donde rho es la masa por unidad de longitud. Por lo tanto, siempre que la gravedad de la superficie sea lo suficientemente grande (con una r pequeña), esta fuerza superará la aceleración centrífuga y no se irá volando. Pero para un toro con un radio pequeño, todo es mucho más complicado.

Decidí usar el método de Monte Carlo para evaluar la forma de equilibrio. Comenzando con la masa total del planeta y el momento angular, distribuí muchos anillos masivos e infinitamente delgados (tomé el potencial de este ejercicio ; es bueno que en física clásica el potencial eléctrico y gravitacional sean los mismos). Calculé su potencial total y agregué centrífugo. Esto nos permite aproximar las superficies equipotenciales y "llenar" el potencial más cerca del centro del toro con un número creciente de anillos, hasta que su masa corresponda a la masa del planeta. Volví a calcular la velocidad angular basada en la nueva distribución de masa. Luego repitió el proceso hasta que el planeta se dispersó, o se comprimió en una bola, o pasaron muchas iteraciones. Este no es el método más elegante (en la literatura se utiliza la descomposición en una serie de armónicos toroidales), pero fue suficiente para mí.

El resultado principal es que un planeta toroidal permite de manera realista una masa y un momento angular suficientemente grandes. La sección no es redonda ni elíptica, sino que se asemeja a un huevo, con una curvatura interna ligeramente más aguda que la exterior.

¿Por qué el planeta no se aplana en un disco? La rotación intenta aplanar el planeta, pero tiene que trabajar contra la gravedad local, que está tratando de comprimirlo en una bola (o cilindro).

Aunque en mi simulación dichos planetas resultaron ser estables, el rango de valores aceptables no fue grande: la mayoría de las combinaciones de masa y momento angular eran inestables. No analicé la compleja cuestión de la inestabilidad nodal.

Consideraré aquí un toroide regordete con una masa igual a la masa de la Tierra y un pequeño agujero central ("Donut"), así como un toroide más ancho, similar a un aro, con una masa de 6 tierras pero más cerca de la gravedad de la Tierra ("Aro").

Donut

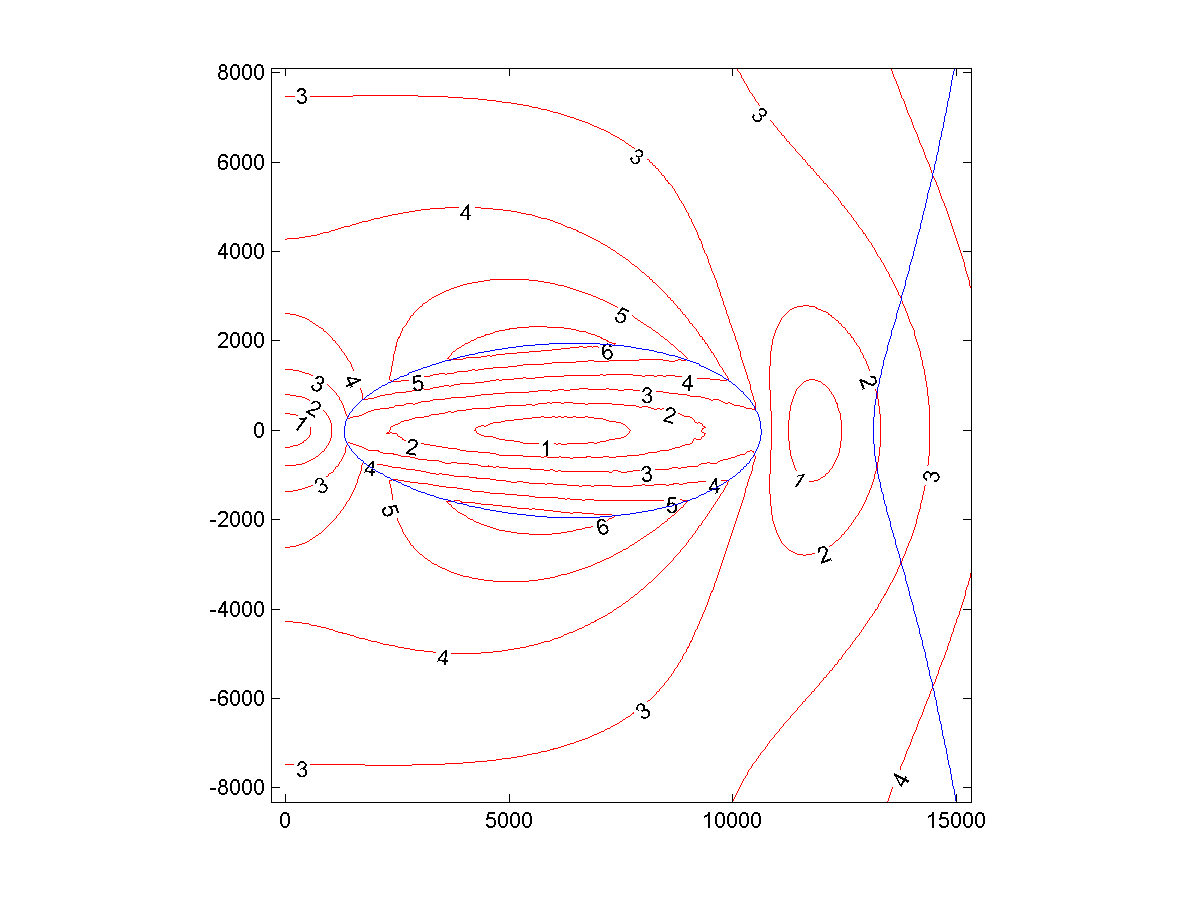Fig. 1: aceleración gravitacional local (m / s ² ) alrededor del Donut, experimentado por un objeto que gira junto con él

El ecuador interno del Donut está a 1305 km del centro y el externo, a 10663 km. El diámetro del ecuador es de 9328 km.

El planeta se extiende sobre una distancia de 1953 desde el plano ecuatorial, y el diámetro de norte a sur es de 3906 km. La relación de diámetro es 2.4.

La circunferencia de norte a sur es 21587 km (0,54 terrestres), y de oeste a este - 66809 km (1,7 terrestres). El área total es 8.2 x 10 ⁸ km ² (1.6 tierra). Volumen total = 1.1 x 10 ¹² km ³ , difiere del de la Tierra en no más del 1% (después de todo, el Donut fue elegido como el planeta de la masa de la tierra). La relación de volumen a área - 1300, 61% de la Tierra - por unidad de volumen de área más.

El día dura 2,84 horas.

Aro

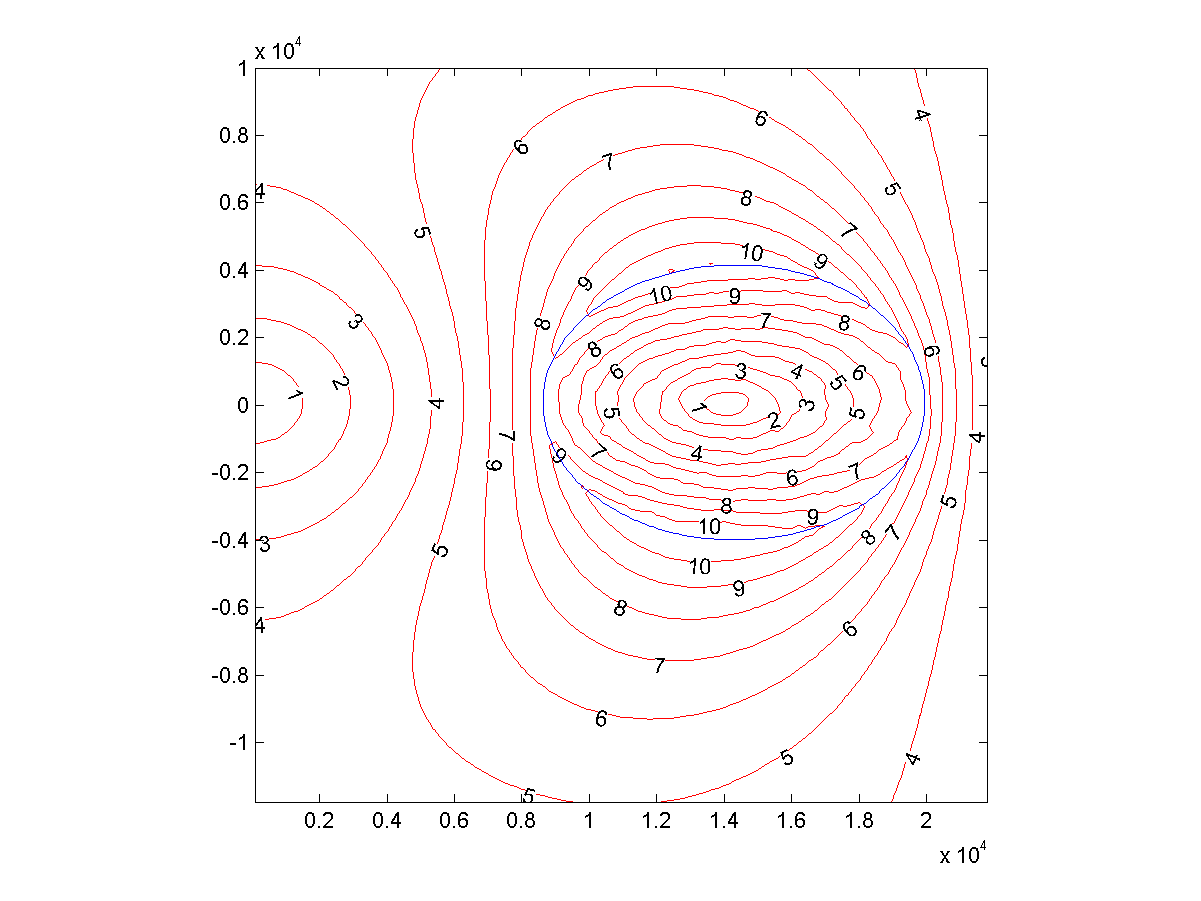
Fig. 2: aceleración gravitacional local (m / s ² ) alrededor del aro, experimentado por un objeto que gira junto con él

El ecuador interno de Hoop está a 8633 km del centro y el externo, a 19937 km. El diámetro del ecuador es de 11.304 km.

El planeta se extiende desde el plano ecuatorial por 4070 km, diámetro de norte a sur - 8141 km. La relación de aspecto de la sección es de aproximadamente 4: 3, como con los monitores antiguos. El radio del círculo del centro de masa es de 14294 km.

La circunferencia de norte a sur es de 30794 km (0,77 terrestres), y de oeste a este - 125270 (3,1 terrestres). El área total de 2.5 x 10 ⁹ km ² , 4.9 veces más grande que la tierra, y el volumen total de 6.5 x 10 ¹² km ³ , 6 veces más grande que la tierra. La relación de volumen a área = 150, 70% de la tierra.

El día dura 3.53 horas.

Medio ambiente

¿Cómo es la vida en una tierra toroidal?

La gravedad

La gravedad superficial depende de la ubicación. Es el más débil a lo largo de los ecuadores internos y externos, y el más fuerte, cerca de los polos, ligeramente hacia el centro. Esta es una de las principales diferencias.

Donut

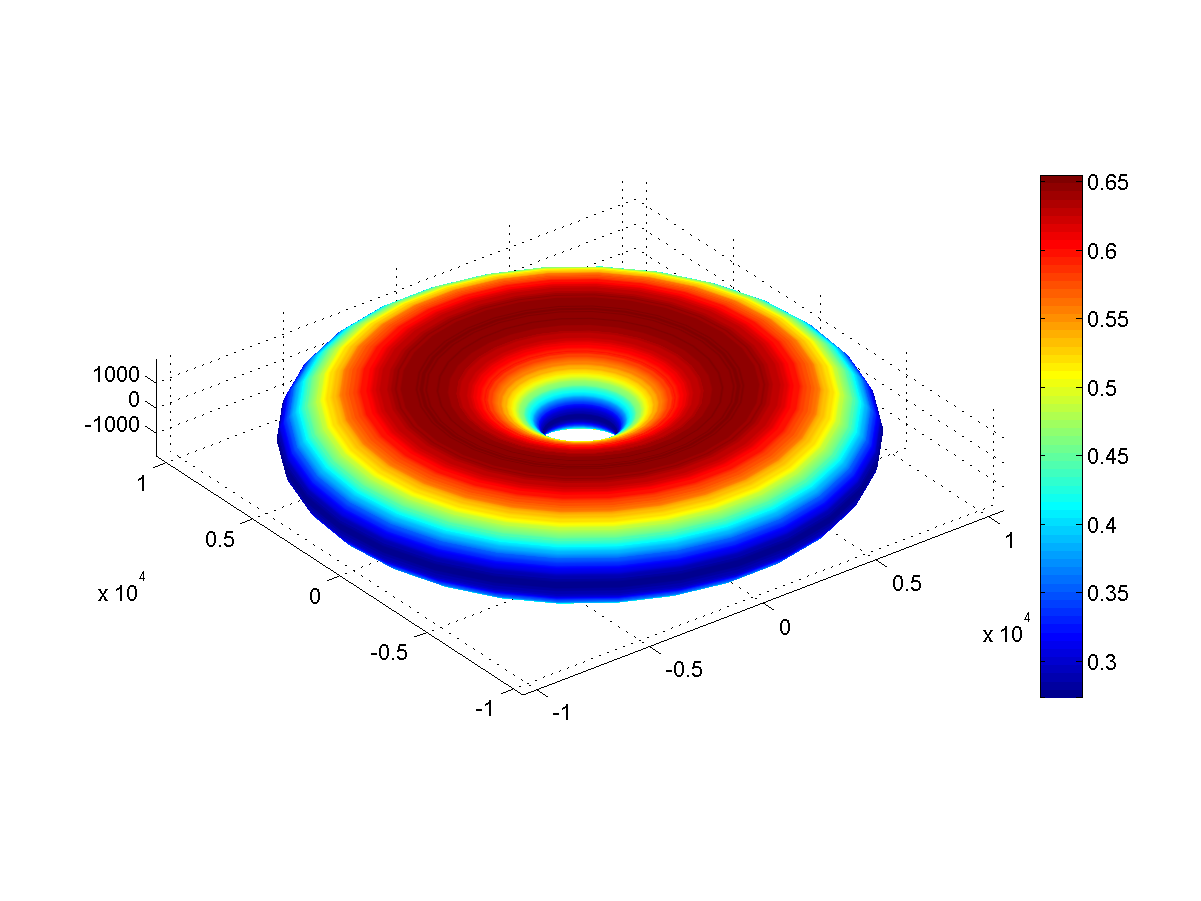Fig. 3: gravedad superficial de la rosquilla (m / s ² )

En Donut, la gravedad a lo largo de los ecuadores es de solo 0.3 G y 0.65 G a lo largo de los polos. La velocidad de escape no es muy diferente de la Tierra, y es igual a 11.4 km / s.

La órbita geosíncrona alrededor del Donut está muy cerca del ecuador externo, a menos de 2000 km. Un satélite que vuela a lo largo de él permanecerá por encima de un lugar, pero, a diferencia de la Tierra, no podrá cubrir todo el hemisferio con engranajes, solo un área pequeña.

Por otro lado, la velocidad periférica en el ecuador es de 6.5 km / s, y los lanzamientos son más fáciles de realizar. Un misil lanzado hacia el este requiere una velocidad de solo 4.9 km / s para escapar.

En el medio del hoyo hay un punto inestable de Lagrange. El satélite allí será atraído hacia el plano ecuatorial, pero cualquier desviación aumentará.

Aro

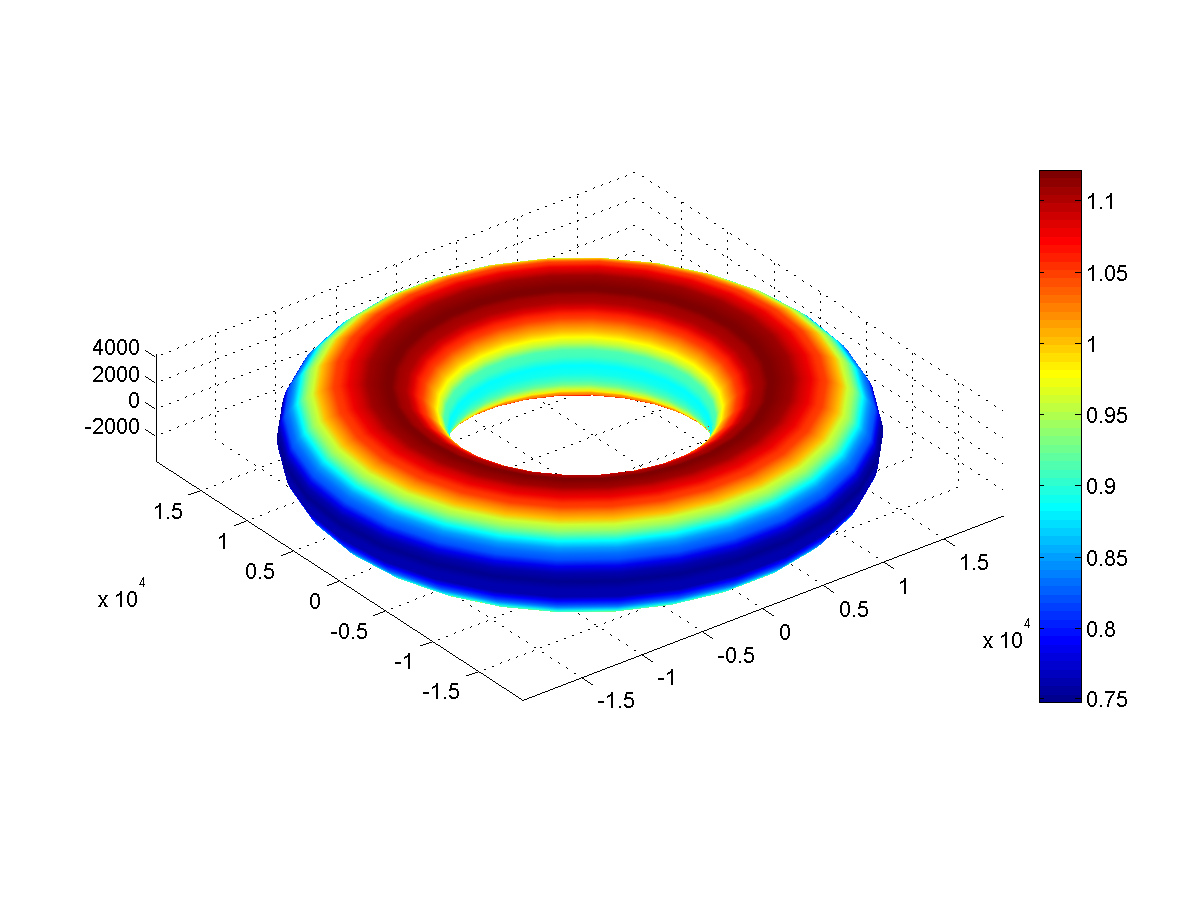Fig. 4: gravedad superficial (m / s ² ) Aro

En Hoop, la gravedad a lo largo de los polos es de 1.1 G, y a lo largo del ecuador externo: solo 0.75 G. En el ecuador interno, es ligeramente más grande, aproximadamente 0.81 G.

La velocidad de escape es de 19 km / s (recuerde que el planeta pesa 6 veces más que la Tierra). En el ecuador externo, la velocidad fuera de control es de 9.9 km / s: un cohete lanzado hacia el este tendrá que recibir una velocidad de 10 km / s.

Una vez más, noto que la baja gravedad en el ecuador y la alta en los polos no significa que las cosas rueden o se arrastren a los polos: como ya se mencionó, la superficie será equipotencial, por lo que la gravedad junto con la corrección centrífuga siempre será perpendicular a ella.

Las masas de aire que fluyen hacia los polos se aplanarán. La diferencia de gravedad creará una diferencia de presión horizontal que, actuando junto con la diferencia de temperatura, creará flujos no triviales.

La luz

Las noches y los días en esos mundos serán muy cortos. El ambiente no tendrá tiempo para enfriarse o calentarse durante los ciclos diarios. Lo que importa es la diferencia en la cantidad de luz recibida durante períodos más largos, es decir, estaciones. Si estos mundos se mueven en una órbita similar a la Tierra alrededor de una estrella similar al sol, será importante.

Si la órbita es más pequeña, las fuerzas de marea pronto harán que estos planetas sean inestables. Dado que el brillo de una estrella aumenta aproximadamente a medida que crece el cuarto grado de su masa, y el radio de la zona viva crece como la raíz cuadrada del brillo, en la zona residencial la escala de las fuerzas de marea será M / (√ (M ⁴ )) ³ = 1 / M ⁵ . Es decir, los efectos de las mareas de las estrellas brillantes serán mucho más pequeños, tal vez sea mejor que Donut y Hoop giren alrededor de una estrella azul y blanca de clase F, y no alrededor de una estrella de clase G, como nuestro Sol, por si acaso.

La parte exterior del planeta toroidal no es muy diferente de la superficie de un elipsoide normal. Llega el día en que sale el sol sobre el horizonte oriental, y la puesta de sol ocurre sobre el oeste. El sol viaja en un gran círculo, moviéndose lentamente de norte a sur y de regreso durante el año, lo que garantiza la disponibilidad de estaciones. Sin embargo, todo es diferente en el interior del planeta. Otras partes del planeta pueden oscurecer el sol; como primera aproximación, se puede esperar menos energía.

Podemos considerar tres casos diferentes: inclinación del eje cero, 23 grados (como la Tierra) y 45 grados.

Inclinación cero

Con una pendiente cero, el lado interno del sol no verá: siempre estará oculto detrás del horizonte o detrás del arco del mundo. En los polos, el sol se mueve a lo largo del horizonte, y un poco más cerca del centro siempre habrá crepúsculo. Las diferencias de temperatura serán grandes, la parte interior del planeta estará sujeta a temperaturas subárticas; esto no es muy diferente del mundo con rotación sincrónica , y en principio, el agua (y posiblemente el dióxido de carbono) siempre debe condensarse en estos lugares. Como resultado, debería haber zonas áridas (posiblemente no demasiado calientes) en el ecuador exterior, posiblemente regiones crepusculares habitadas cerca del polo y un interior helado.

Inclinación de 23 grados

Fig. 5: Temporadas de donas en primavera, verano, otoño e invierno

Para una pendiente de 23 grados, coincidiendo con la tierra, la primavera y el otoño coincidirán con una pendiente cero: luz a lo largo del ecuador y oscuridad en el interior, cerca del agujero. En verano e invierno, el sol tendrá la oportunidad de penetrar detrás del borde, en el lado opuesto del hoyo. También habrá grandes áreas con el sol a medianoche o con la noche eterna en verano o invierno. En la Tierra, las regiones polares son pequeñas, pero aquí serán círculos largos y continuos.

Los amaneceres de primavera y el crepúsculo de otoño en el interior deberían dar colores asombrosos y profundos, porque el sol se elevará a través de la atmósfera al otro lado del planeta (previamente salido o puesto, si puedo decirlo). Todo esto, junto con los efectos ópticos atmosféricos locales, producirá rojos y gradientes muy profundos. Inmediatamente antes o después del atardecer o el amanecer, se verán partes de la corona solar.

Este espectáculo habría sido más impresionante si no hubiera sido tan corto. En la Tierra, el sol pasa unos 15 ° por hora. En el caso más rápido, el sol pasa uno de sus diámetros en 2.1 minutos. En el Donut, el sol irá 127 ° por hora, y en Obruch - 102 °. El amanecer y el atardecer tomarán 15 o 19 segundos respectivamente. El ángulo inclinado y los retrasos atmosféricos prolongarán ligeramente la vista, pero para un residente de la tierra será demasiado corto.

Si te paras en el lado interno de la superficie y miras hacia arriba, el otro lado ocupará 20 grados del cielo en Obruch y 30 grados en el Donut, un enorme arco que atraviesa todo el cielo.

¿Por qué donut no es mucho más ancho? Es muy plano, por lo que se ve más corto en el cielo. Esto, por cierto, significa que cuando la luz solar se refracta a través de la atmósfera del otro lado durante el amanecer o el atardecer, los colores rojos serán mucho más profundos que en Obruch.

Dentro de la parte opuesta iluminada del toro se iluminará todo a la luz de la luna. Pero la superficie será mayor, por lo que las noches serán mucho más brillantes. En Obruch, la luz será 16,000 veces más fuerte que la Tierra (8,000 lux) cuando toda la parte opuesta esté iluminada (tomemos el albedo igual a la Tierra), y la noche será como un día nublado. En Donut, la iluminación alcanzará una luz tenue (12,000 lux). Pero esta es la situación del lado opuesto completamente iluminado: durante el equinoccio solo se verá una tira delgada.


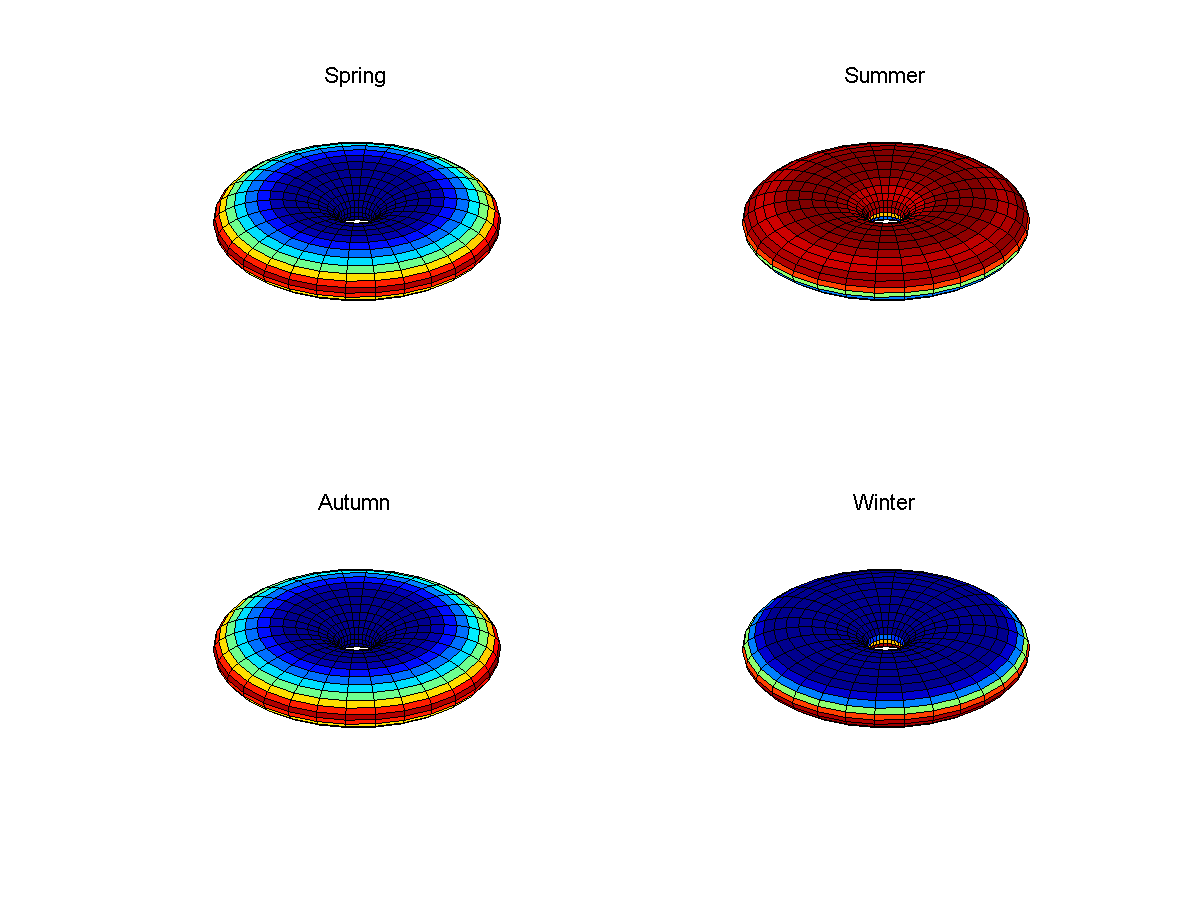Fig. 6: iluminación diaria promedio en el Donut durante la primavera, verano, otoño e invierno para el caso con una pendiente de 23 grados

En el caso del Donut, una superficie bastante plana significa que el hemisferio norte o sur (uno y medio) recibirá mucha luz solar. El calentamiento total del planeta será mayor durante estas estaciones que durante la primavera y el otoño, a diferencia de la Tierra, donde es constante, porque el área que recibe luz permanece constante. También se observarán efectos no triviales debido a los ángulos entre la superficie y la luz solar, y las zonas templadas recibirán un poco menos de energía que las regiones polares y los trópicos.

En los trópicos exteriores habrá aproximadamente la misma afluencia de energía solar. Hacia los polos, la estacionalidad se siente con mayor fuerza: los trópicos en verano reciben más energía que el ecuador en cualquier momento. Los inviernos serán igual de oscuros. En los polos y detrás de ellos, en el interior, en lugares con máxima gravedad, el sol será visible durante seis meses, y luego habrá una noche polar. Aquí el clima cambiará dramáticamente: en los trópicos exteriores, al menos, habrá noches durante 1,5 horas, y aquí durarán 6 meses. Finalmente, más cerca del ecuador interno al lado del agujero, el día y la noche serán iguales en invierno (y también se agregará la luz reflejada por el otro lado), por lo que la temperatura será un poco más alta.


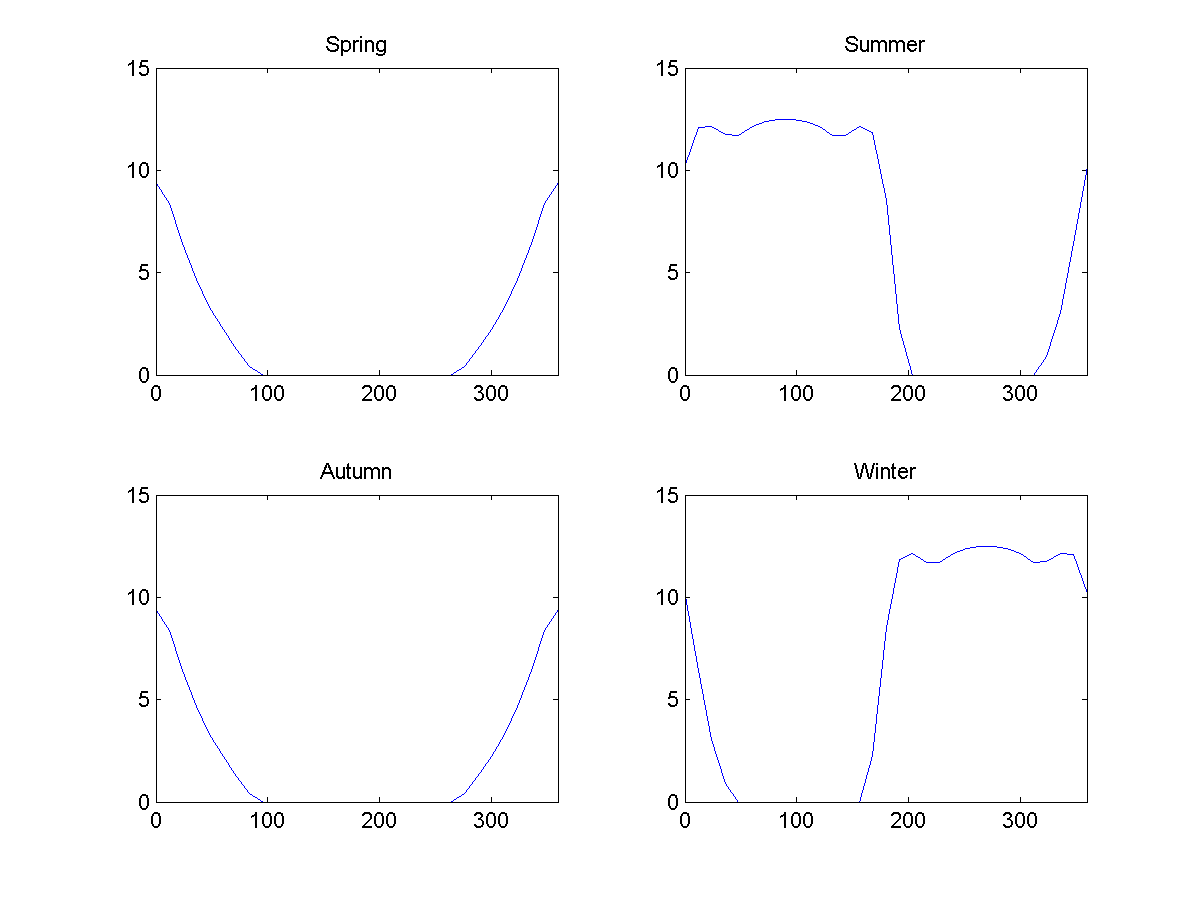Fig. 7: iluminación promedio durante diferentes estaciones en el Donut, en función de la latitud en el caso de 23 grados. 0 representa el ecuador externo, 90 representa el polo norte, 180 representa el ecuador interno, 270 representa el polo sur.

Una gran diferencia en la cantidad de energía recibida en el lado soleado del verano del hoyo y en el lado oscuro del hoyo del invierno conducirá a un clima severo, pero debido a otras rarezas de estos mundos, será más difícil igualar la diferencia de energía que en la Tierra.

En promedio, la parte externa ecuatorial recibirá 2.5 veces más energía que las partes polares, y la parte interna recibirá cuatro veces menos energía que las áreas circundantes.


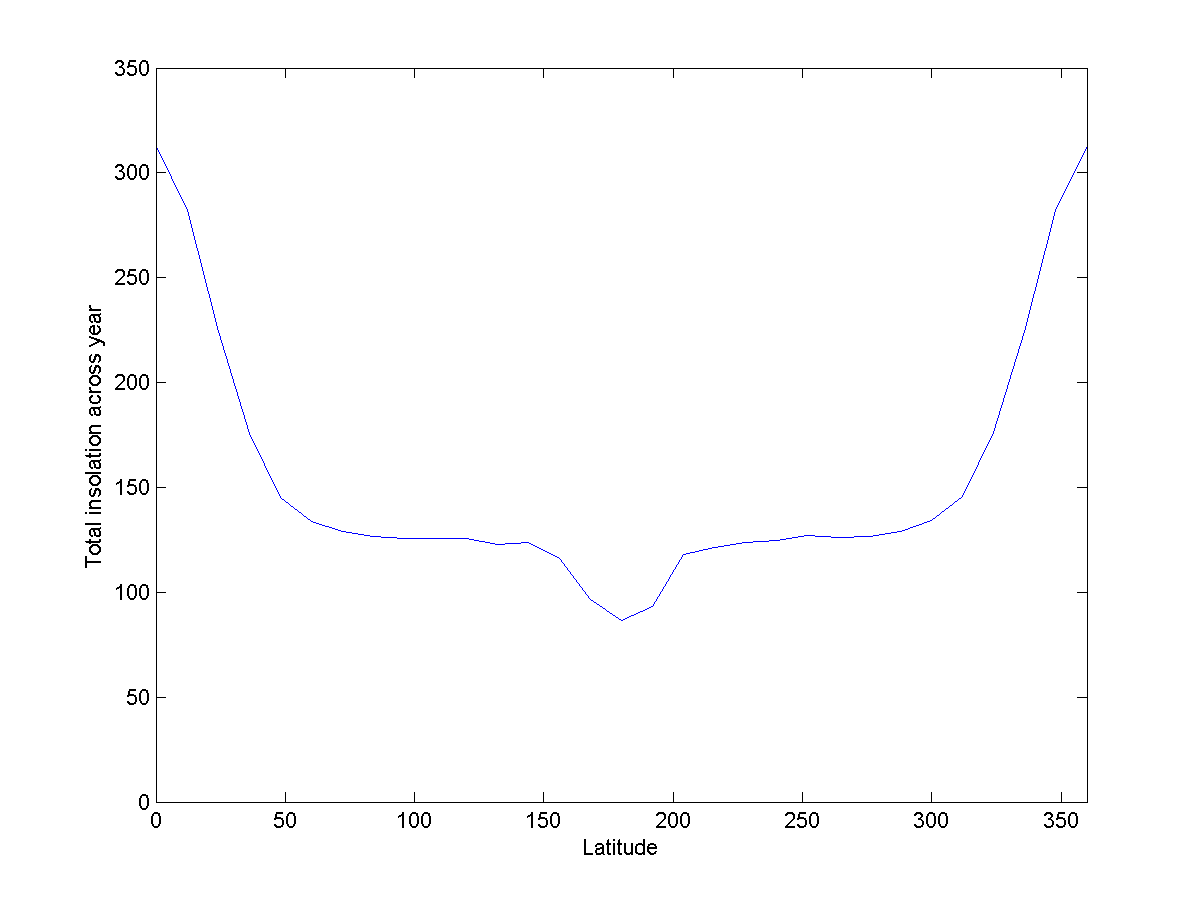Fig. 8: energía en diferentes latitudes del Donut

El aro proyecta menos sombra sobre sí mismo. Más importante aún, no es tan plano como el Donut.


Fig. 9: iluminación promedio durante el día en Obruch, 23 grados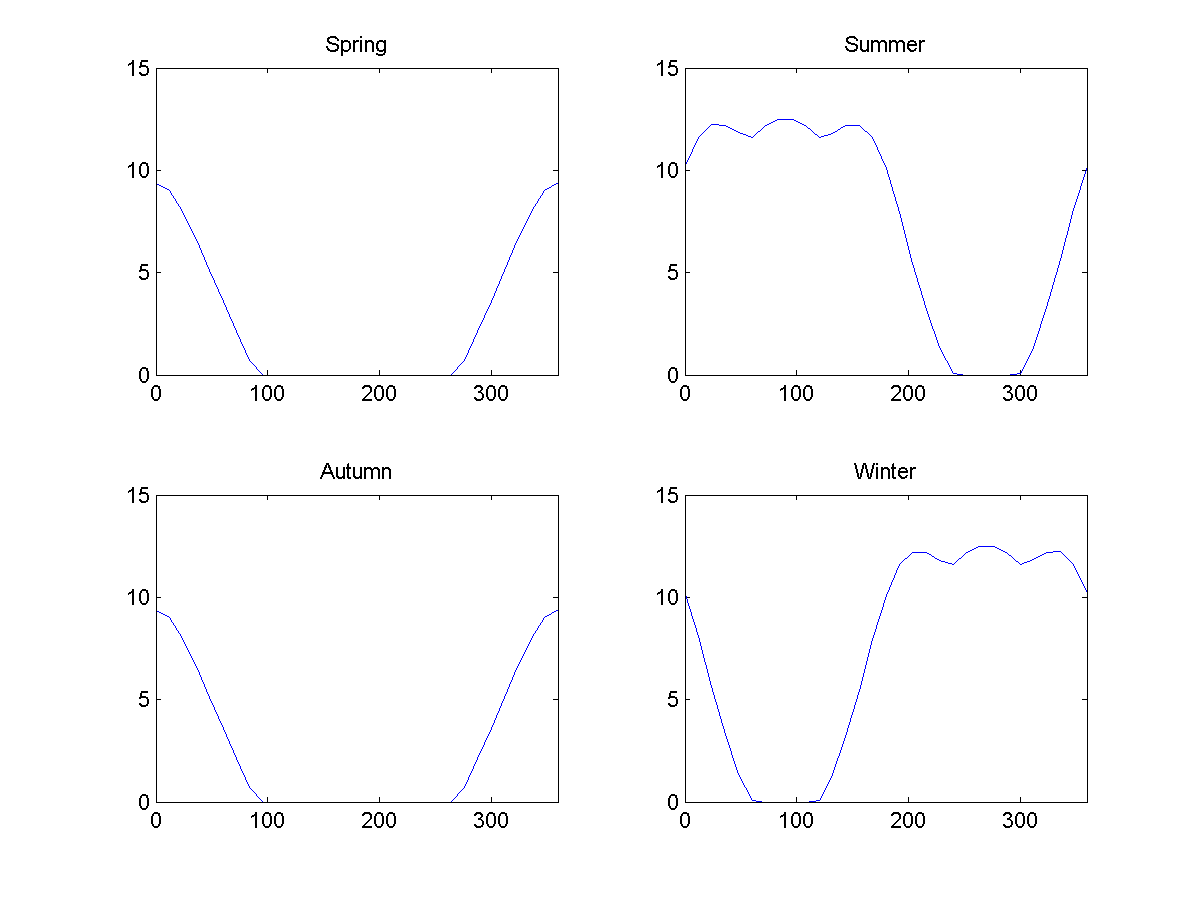


Fig. 10: iluminación promedio durante diferentes estaciones en Obruch, en función de la latitud en el caso de 23 grados. 0 representa el ecuador externo, 90 representa el polo norte, 180 representa el ecuador interno, 270 representa el polo sur.

A primera vista, las estaciones se ven como se esperaba. En primavera y otoño, las partes internas estarán ocultas a la sombra, en verano e invierno, una región polar se ilumina más intensamente, y la otra es más débil, y las partes internas recibirán su iluminación. Esto conducirá a la presencia de un ciclo estacional en la parte interior del planeta, que irá dos veces más rápido que en el exterior (esto será así en Donut): el clima será cálido en julio y enero.


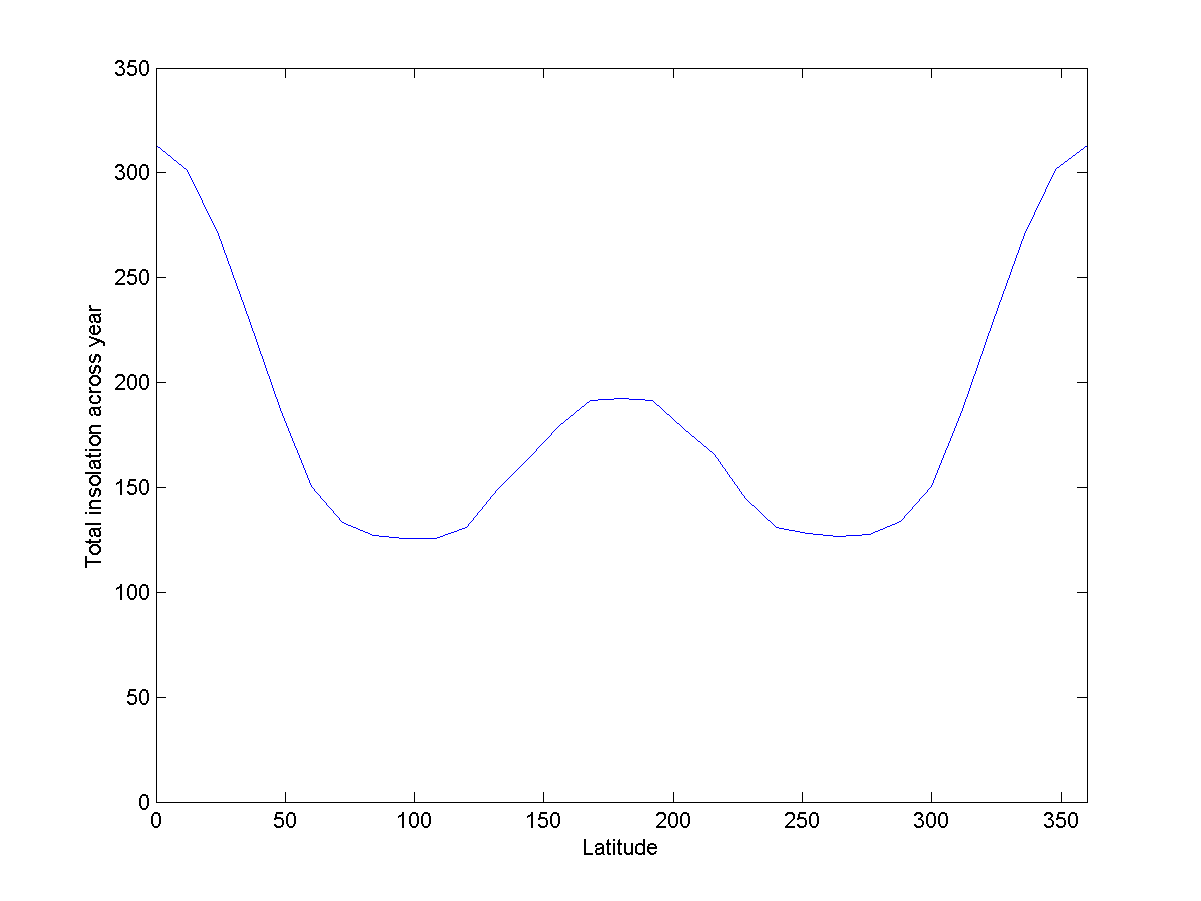Fig. 11: energía recibida durante el año en diferentes latitudes del aro

En comparación con Donut, esto no será intuitivo: el ecuador interno recibe más luz durante el año que las regiones polares. , – , . 60%.

45

, – , !

, , 90 – , . , . , . – . , .


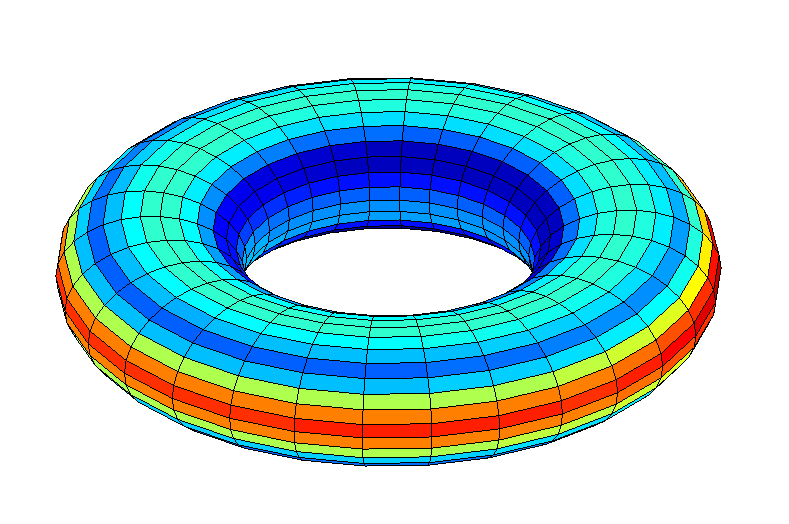. 12: , 45

, 10% . .

, . .

, ( 1300 , 1500 , – 2124 ). , , . - . 6 , , 5 .

. , r R 2 π r , r/R. , , 43% . – 12% ! , , , , , . .

. , 1,5 ( 12 ), 3 (24 ). , .

. , , . - , .

, , , . , .

, , , . , «» , , : , , . : , , .

8 , . , , . , , , , . , – .

, (Intertropical Convergence Zone, ITCZ) , , , (), , , ( ). , , ITCZ , . , 30 ( , , ).

, , . : , , , .

, , . 1,5-3 , , .

, . – . ( ). , .

, , 6 , 5 , 20% - ( 20%). , , .

: , . ; , , . , . , , . , , .

: , . 150% . (133% , 90% ). .

, . , , . , , (, , ). , , – .

¿Podrán estos mundos sostener la luna?

La luna que orbita en el plano del ecuador en una órbita circular cerca del toroide no sentirá ninguna diferencia con respecto a un planeta redondo. Sin embargo, al adquirir excentricidad, las cosas se complicarán. Un campo potencial al acercarse a un planeta cae más lento que 1 / r, como en los planetas normales: la elipse de Kepler ya no es adecuada como solución. Con la inclinación de la órbita, el sistema se vuelve aún más complejo: ahora la luna sentirá la planeidad del planeta.

En cierto sentido, los desarrolladores de satélites ya se enfrentan a un problema similar: la Tierra está lo suficientemente aplanada en los polos para que sea notable. Este problema se resolvió en las primeras etapas de los viajes espaciales (Wikipedia, (Tremaine y Yavetz 2013) o (Nielsen, Goodwin y Mersman 1958).

De hecho, una órbita elíptica está sujeta a precesión: cambia gradualmente de dirección y, en el caso de la Tierra, esto depende de la inclinación de la órbita. La excentricidad también puede nadar. En cualquier caso, para un toroide, estos efectos serán más pronunciados. Serán tan fuertes que los métodos de cálculo estándar ya no funcionarán, y tendremos que realizar simulaciones por computadora.

Estoy seguro de que las lunas en órbitas circulares suficientemente remotas se comportarán de manera bastante estable. Lo más probable es que estén sujetos a la precesión, por lo que su órbita será más como un zócalo que una elipse, pero no volarán de las bobinas. Por supuesto, si la órbita de la luna está más cerca, todo será diferente.

En la simulación (no utilicé un toro completo, sino un anillo de 30 masas) se me abrieron varias posibilidades. La órbita elíptica ecuatorial se ve ordenada y estable, pero la precesión la convierte en una cuenca.



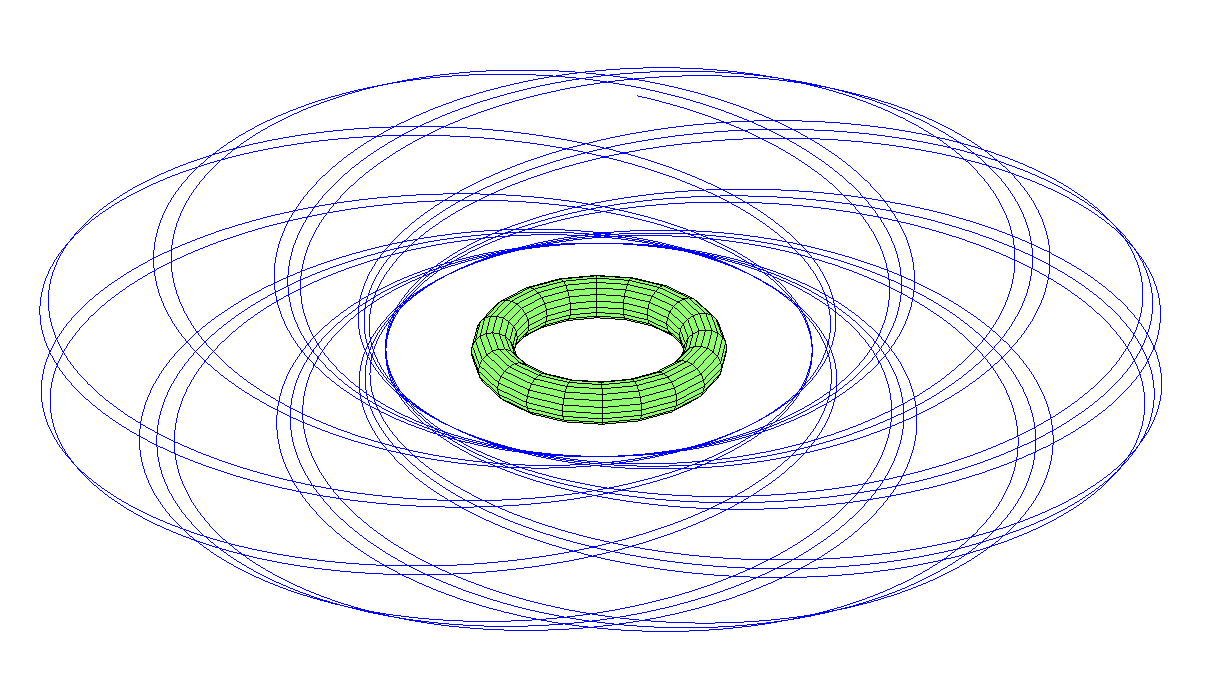
La órbita circumpolar precesiona aún más, no solo aparece la salida, sino también la precesión del avión. La luna en el cielo puede aparecer en cualquier constelación.



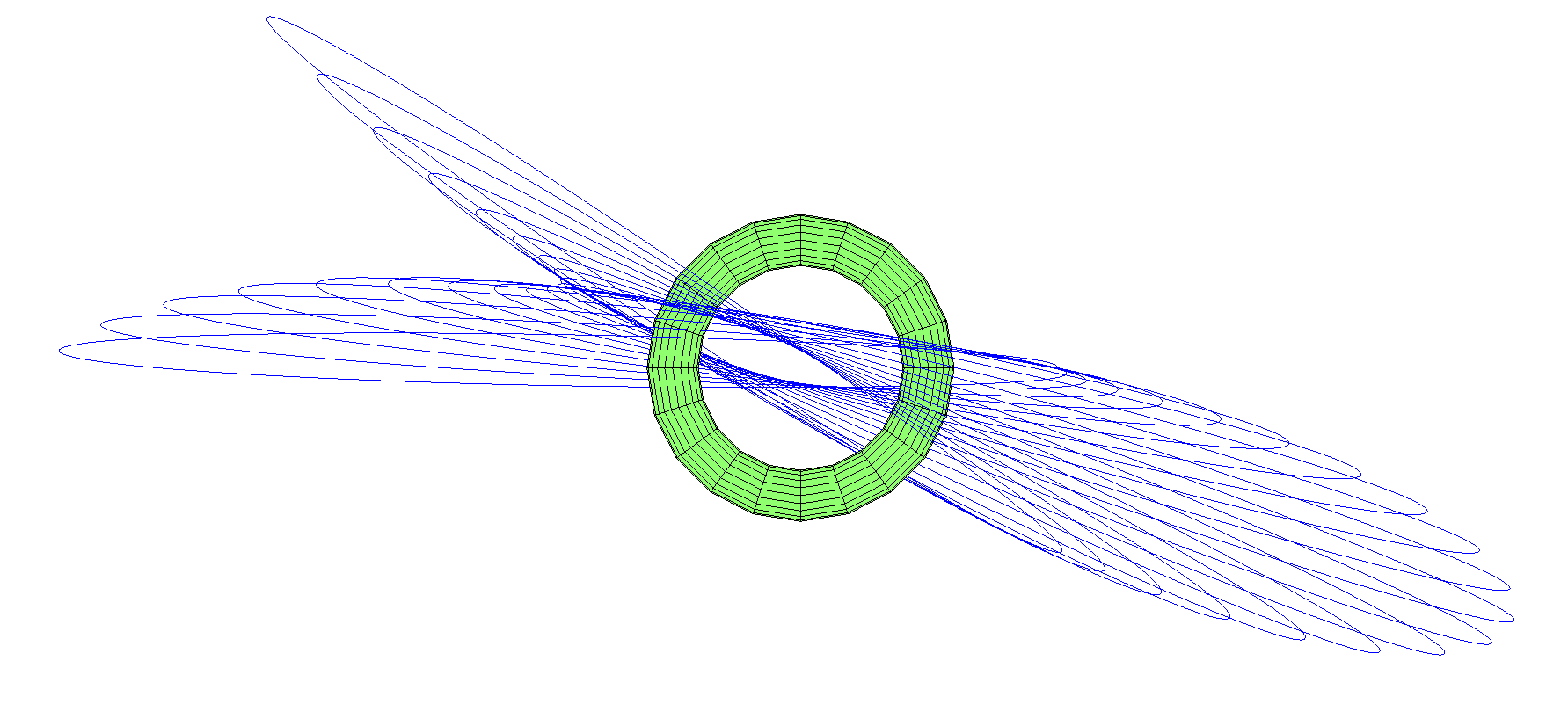
¿Qué pasa con las órbitas que pasan por el agujero? Como señalé anteriormente, el centro geométrico es un punto inestable de Lagrange. Si coloca la luna allí, cualquier golpe la sacará de allí. Pero hay órbitas de aspecto estable a través del centro (más precisamente, bajo cualquier impacto, se convertirán en otra órbita de forma similar). La opción más simple es la luna, que cuelga de un agujero a otro, como un péndulo:



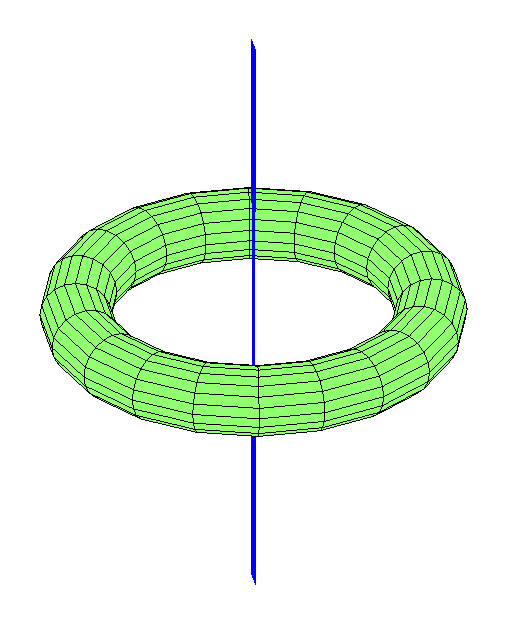
Puedes imaginar la luna volando a cierta longitud:



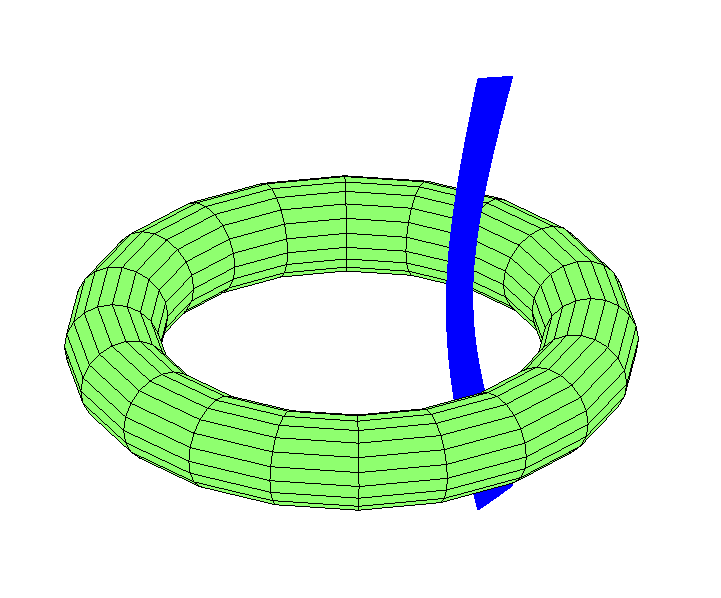
Con la adquisición de la velocidad en longitud, se moverá en el hoyo:



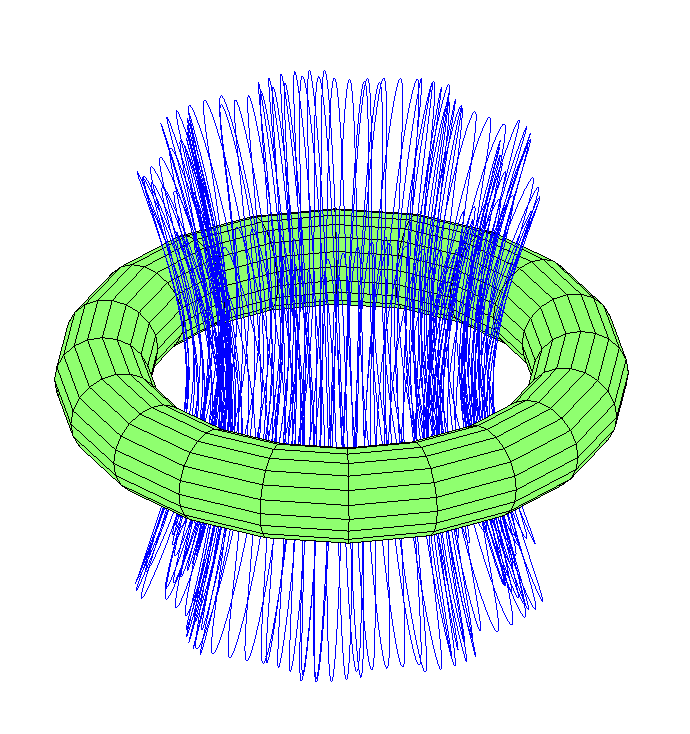
¿Qué pasa con las trayectorias que pasan por un agujero en una dirección? Resultó que hay bastantes ocho órbitas que dibujan una gran bola toroidal.





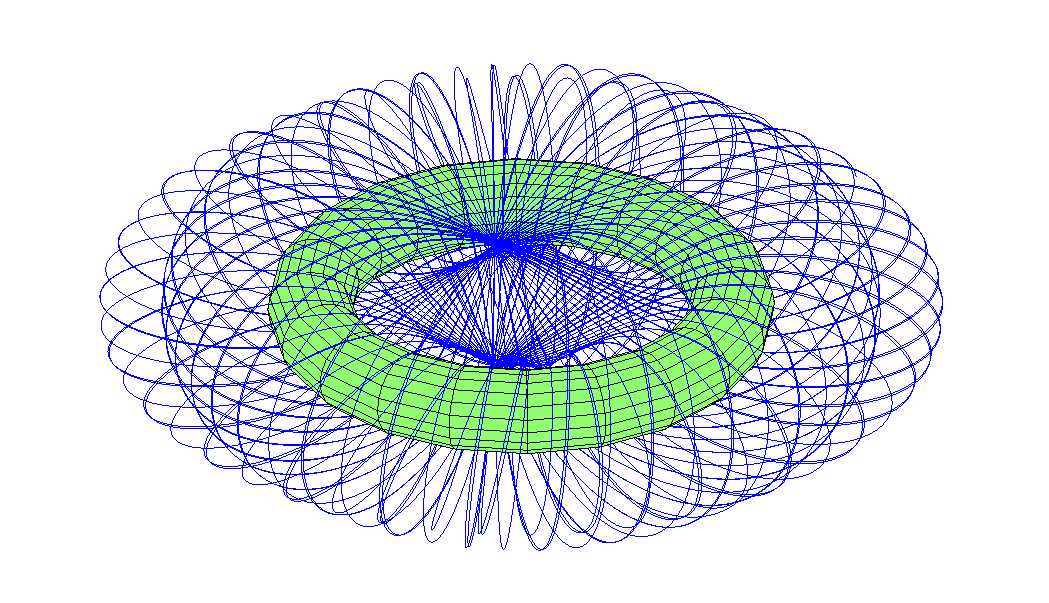
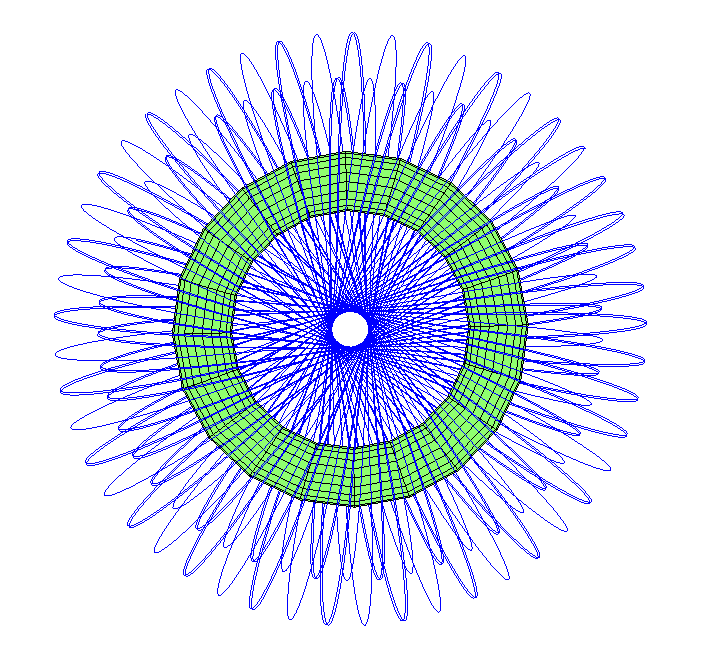
Tenga en cuenta que la órbita es ligeramente alargada. Desde el "apogeo", por encima del ecuador externo, pasa a través de un agujero, aparece en el reverso, donde experimenta un perigeo en un punto opuesto al inicial. Luego, nuevamente pasa a través del agujero y sale al lado del lugar donde comenzó a moverse, pero la precesión lo retuerce a lo largo del toro.

Estas simulaciones deben tomarse como borradores primarios: los cálculos reales requieren una mayor precisión. Mi precisión numérica no es suficiente para evaluar la estabilidad a largo plazo. Los campos gravitacionales de Donut y Hoop parecen aún más complicados debido a su aplanamiento, y el sol y otros planetas también contribuirán.

Fuerzas de marea

Las fuerzas de marea son un problema. Imagina una luna moviéndose alrededor de un toroide. Una hinchazón de agua y piedra se forma detrás de él. La rotación rápida empujará la hinchazón hacia delante de la luna (si la luna se mueve en la dirección de rotación del planeta y está por encima de la órbita geoestacionaria). La atracción del bulto arrastrará a la luna hacia adelante, dándole aceleración, y en el espacio esto hace que la luna se mueva en una órbita más alta. Así es como la Luna adoptó una gran cantidad de momento angular de la Tierra, ralentizó su rotación y se alejó de ella. En el caso de una rotación rápida, como en nuestros toroides, el efecto será más notable: las lunas volarán lejos del planeta y es probable que se pierdan.

¿Qué pasará con las lunas cercanas, debajo de la órbita geoestacionaria? Se moverán más rápido que la hinchazón, lo que los ralentizará. La órbita caerá. Pronto descenderán en espiral y se convertirán en meteoritos gigantes. Lo mismo sucederá con las lunas que se mueven en la dirección opuesta. Por supuesto, si la luna es lo suficientemente grande, las fuerzas de marea pueden romperla y convertirla en un anillo.

Es probable que las órbitas más anchas que pasan por el agujero pierdan estabilidad. Las órbitas del péndulo adquirirán un momento angular debido a una hinchazón, y la luna se moverá cada vez más rápido hasta que se aleje del planeta o caiga. Unas ocho órbitas pueden entrar en resonancia y ganar y perder energía en partes iguales, pero un problema similar les espera. Entonces, lo más probable es que los toroides no tengan lunas realmente exóticas. Sin embargo, nadie prohíbe lanzar satélites artificiales con soporte de órbita. Las órbitas de péndulo pueden ser útiles para los satélites de comunicación en la superficie interna de un toro.

Resumen

Es poco probable que los mundos toroidales aparezcan naturalmente. Pero si lo hacen, serán lugares increíbles para buscar aventuras. Gran superficie. Regiones con climas, estaciones, gravedad y ecosistemas muy diferentes. Increíble cielo por dentro. Clima desenfrenado. Luna en órbitas extrañas.

Sería bueno aprender cómo crearlos no solo en simulaciones.

Anders Sandberg es investigador, académico, futurólogo, transhumanista y escritor. Recibió su doctorado en Neurobiología Computacional de la Universidad de Estocolmo, y actualmente es miembro de la Sociedad de Investigación James Martin de la Universidad de Future Humanity de la Universidad de Oxford.