El universo comenzó no con el Big Bang, sino con el Big Thaw

Constante cosmológica y creación del universo.

Con respecto al Universo, hay dos acertijos sin resolver particularmente dolorosos, uno de los cuales está relacionado con su destino final, y el segundo, con el comienzo, cosmólogos intrigantes durante décadas. La comunidad científica siempre ha creído que estas dos tareas son independientes entre sí, pero ¿y si no lo es?

La primera tarea está relacionada con la existencia de algo llamado "energía oscura", que hoy acelera la expansión del Universo, y finalmente determina su destino final. Los teóricos dicen que la acción de la energía oscura puede explicarse introduciendo un nuevo término en las ecuaciones de Einstein llamado "constante cosmológica". Pero para que esta explicación funcione, la constante cosmológica debe tener un cierto valor, muy pequeño. En unidades naturales, está determinado por una unidad dividida por un número que consta de 123 dígitos. Una explicación del valor de esta constante es uno de los problemas más difíciles de la física teórica.


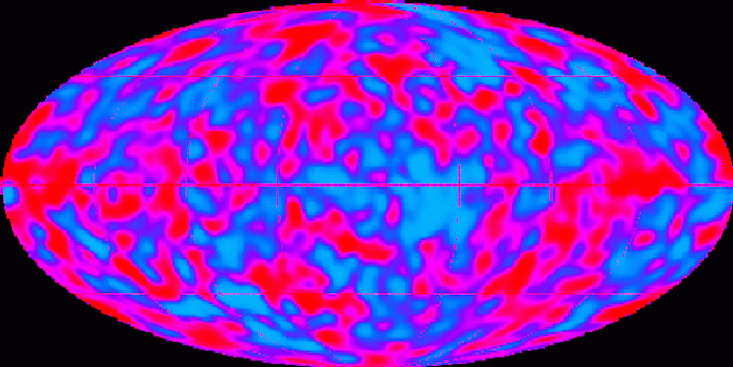Las variaciones de CMB indican fluctuaciones de densidad en el Universo temprano

El segundo problema está asociado con otro número importante que define nuestro Universo y con la formación de estructuras como galaxias y grupos de galaxias. Sabemos que el Universo temprano, aunque era muy homogéneo, contenía pequeñas fluctuaciones en la densidad, que se convirtieron en las causas fundamentales de las estructuras cósmicas que vemos hoy. Para coincidir con nuestras observaciones, estas fluctuaciones tenían que tener un cierto tamaño y forma. Cómo aparecieron estas fluctuaciones en los primeros períodos de la evolución del Universo, y su forma y tamaño, es un misterio igualmente sorprendente de la cosmología.

Dado el enfoque generalmente aceptado de la cosmología, estos dos números (la magnitud de la constante cosmológica y la magnitud de las perturbaciones iniciales) no se consideran relacionados. Después de todo, uno de ellos trata con la fase más temprana del universo, y el segundo con la última, y ​​están separados por un tiempo cósmico de 14 mil millones de años. Además, la cosmología estándar no explica estos valores sobre la base de principios fundamentales. Los modelos generalmente aceptados del Universo no dicen nada sobre el valor numérico de la constante cosmológica, o predicen valores completamente diferentes. Con respecto a la magnitud de las perturbaciones iniciales, el enfoque más popular es obtener este valor de la clase de modelos que describen la inflación, un período de rápido crecimiento en la fase temprana de la existencia del Universo. El problema con los modelos inflacionarios es que pueden ajustarse para producir casi cualquier resultado, por lo que carecen de capacidad predictiva.

En mi trabajo reciente, llevado a cabo con mi hija, Hamsa Padmanabhan y Tomalla Fellow en la Escuela Técnica Superior Suiza de Zurich, ambos números están asociados con la cosmogénesis, la creación del Universo, y se explica su significado exacto. Nuestro trabajo, publicado recientemente en Physics Letters B, muestra que la existencia misma de una constante cosmológica, así como su pequeño valor, puede representarse como una consecuencia directa del contenido de información del espacio-tiempo [Padmanabhan, T. y Padmanabhan, H. Información cósmica, la cosmológica constante y la amplitud de las perturbaciones primordiales. Physics Letters B 773, 81-85 (2017)]. Además, el análisis proporciona el valor correcto para el tamaño y la forma de pequeñas fluctuaciones del Universo temprano.

La notable interconexión de estas constantes fundamentales es esencial para nuestra comprensión del universo. En particular, cambia nuestra comprensión del Big Bang y elimina la necesidad de un período de inflación en las primeras etapas del universo.

El Big Bang es probablemente la característica más famosa de la cosmología estándar. Pero tampoco es realmente necesario para ella. El modelo clásico del Universo, descrito por las ecuaciones de Einstein, deja de funcionar bajo las condiciones del Big Bang, a una densidad y temperatura infinitas; esta es la situación que los físicos llaman singularidad.

Pero, ¿y si no hubiera singularidad? Desde la década de 1960, los físicos han estado trabajando para describir el Universo sin el Big Bang, tratando de combinar la teoría de la gravedad y la teoría cuántica en algo llamado "gravedad cuántica". Los físicos John Wheeler y Bryce DeWitt fueron los primeros en aplicar estas ideas a la hipotética fase dogométrica del Universo, en la que los conceptos de espacio y tiempo aún no han surgido de una estructura desconocida. Esto condujo a la aparición de la cosmología cuántica, en la que los físicos intentan describir la dinámica de modelos simples de juguete del universo en lenguaje cuántico. Huelga decir que, a lo largo de las décadas, han aparecido repentinamente varias ideas diferentes, aunque relacionadas, para describir la fase pregeométrica. Lo que los une es que el Universo clásico sin ninguna singularidad aparece a través de una serie de transformaciones de la fase pregeométrica a aquella en la que el espacio-tiempo es descrito por las ecuaciones de Einstein. La principal dificultad para construir tal descripción es que no tenemos una teoría completa de la gravedad cuántica que nos permita modelar la fase pregeométrica en detalle.


Einstein calificó su adicción a la constante cosmológica varias veces como un grave error en sus ecuaciones. Hoy, los físicos creen que tiene un significado positivo.

El ingrediente clave que presentamos para ayudar a sortear esta complejidad técnica es el concepto de información espacial. Recientemente, la idea de que la información debe desempeñar un papel clave en la descripción de la física está ganando cada vez más apoyo. Aparece en varios casos cuando los científicos intentan combinar los principios de la teoría cuántica y la gravedad, por ejemplo, en el estudio de los agujeros negros cuánticos. Además, en algunos de estos modelos existe una idea intrigante de la holografía, que establece que el contenido de información de una región grande puede estar relacionado con el contenido de información de sus fronteras. Pero, desafortunadamente, la descripción matemática de la información en diferentes casos es diferente, y el principio unificador, aplicable en todos los casos, aún no se ha encontrado. Por lo tanto, para aplicar la idea de información a todo el Universo, primero teníamos que encontrar una definición físicamente apropiada para ello.

La definición de información espacial que utilizamos puede describirse por analogía. Cuando un trozo de hielo se derrite y se convierte en agua, hay una transición de fase de sólido a líquido. Los procesos de transición de fase reales pueden ser extremadamente complejos, pero el número total de átomos de hielo será el mismo que el número de átomos de agua. Este número determina el número de grados de libertad del sistema que no cambia durante la transición de fase. Exactamente de la misma manera, la transición de fase que condujo a la aparición del Universo puede describirse mediante un número que relaciona el número de grados de libertad en la fase pregeométrica con la cantidad inherente en el espacio-tiempo clásico. Usando este número, que llamamos CosmIn, podemos combinar las dos fases del universo y evitar las complejidades del modelo completo de gravedad cuántica.

Cosmin, como número físicamente observable, debe ser finito. En ausencia de singularidades, creemos que todas las cantidades físicas deben ser finitas. Además, pudimos demostrar que el cosmo será finito solo si el Universo experimenta una fase acelerada de expansión en el último período de existencia, como observamos hoy. Esta conexión no solo indica la existencia de una razón fundamental para la existencia de una constante cosmológica, sino también acerca de los métodos para calcular su valor numérico, si conocemos el valor de la cosmina.

El valor de cosmin en la fase pre-geométrica o gravitacional cuántica del Universo se puede determinar utilizando los resultados que aparecen periódicamente en diferentes modelos de gravedad cuántica. Resulta que la cantidad total de información transferida desde la fase gravitacional cuántica a la fase clásica debería ser igual a un número simple: 4π, el área de una esfera de radio unitario. Usando este hecho, podemos relacionar el valor numérico de la constante cosmológica con la escala de energía, en la cual el Universo pasó de la fase gravitacional cuántica a la clásica.

Esta escala de energía de la transición puede asociarse con la segunda propiedad misteriosa de nuestro Universo: la magnitud de las pequeñas fluctuaciones cuánticas en el Universo temprano que crecieron y formaron las galaxias y los cúmulos galácticos que vemos hoy. Un sistema popular para calcular el tamaño de estas fluctuaciones utiliza modelos inflacionarios del Universo que describen el Universo pasando por una increíble expansión grande y rápida de tamaño. Pero hay muchos modelos inflacionarios y son muy diferentes, y pueden dar el valor deseado. También vale la pena señalar que la forma de las fluctuaciones iniciales fue obtenida por Edward Robert Harrison en 1970 (e independientemente por Jacob Zeldovich), y se llama espectro de Harrison-Zeldovich. ¡Pero la gente olvida señalar que Harrison obtuvo su resultado hace más de diez años antes de la invención de modelos inflacionarios!

Nuestro modelo nos permite relacionar ambas cantidades, el valor de la constante cosmológica y el tamaño de las fluctuaciones iniciales, con la escala de energía en la que el Universo pregeométrico experimentó una transición de fase y se convirtió en el Universo clásico en el que vivimos. Y, atención, cuando seleccionamos la escala de energía correcta, obtenemos el valor correcto y observado para ambos valores. Esto nos lleva a una relación algebraica entre la constante cosmológica, la magnitud de las fluctuaciones iniciales y la cósmica. Podemos voltear esta relación usando los parámetros cosmológicos observados y verificar si el valor del cosmo es realmente 4π. La teoría pasa la prueba perfectamente; encontramos que el cosmo determinado a partir de las observaciones es 4π con una precisión de 1/1000.

Sorprendentemente, una combinación compleja de parámetros cosmológicos, considerados no relacionados entre sí, tiene un significado tan simple. Un enfoque común sería considerar dicha relación como una coincidencia aleatoria. Creemos que ella nos está diciendo algo profundo y hermoso sobre nuestro universo.

Creemos que hicimos el primer intento de relacionar el valor numérico de la constante cosmológica con el tamaño de las fluctuaciones en el Universo temprano, y de obtener ambos valores de un modelo que no tiene parámetros ajustables y los asocia con la escala de energía en la que el Universo comenzó a existir.

Todas estas ideas existen en una plataforma más general de gravedad cuántica, una teoría que los físicos, a pesar de casi cinco décadas de desarrollo, todavía no tienen. Una de las ventajas de nuestro modelo es que no requiere los detalles de la gravedad cuántica. Pero ella da dos pistas importantes sobre la naturaleza de la gravedad cuántica y la estructura del espacio-tiempo. En primer lugar, ella dice que el espacio-tiempo debe ser representado como un grado de libertad microscópico, así como la materia que consiste en átomos. En segundo lugar, argumenta que la teoría correcta del origen del universo debería incluir una transición de fase desde la fase pregeométrica a la fase clásica.

Estos consejos pueden responder una pregunta clave: ¿por qué, después de varias décadas de trabajo, los teóricos no han combinado la gravedad y la teoría cuántica? Creemos que esto se explica mejor por otra analogía. Sabemos que la dinámica de fluidos es una teoría física consistente expresada a través de un conjunto de ecuaciones. Si los tomamos como fundamentales y les aplicamos los principios de la teoría cuántica, podemos descubrir un nuevo fenómeno interesante, por ejemplo, los fonones (cuantos de vibración) y sus interacciones. Sin embargo, utilizando este enfoque, no podremos llegar a la estructura cuántica de la materia.

Existe evidencia de que las ecuaciones que describen la gravedad en este sentido son similares a la dinámica de fluidos. En otras palabras, reformular las ecuaciones que describen la gravedad utilizando los principios de la teoría cuántica es similar a aplicar principios cuánticos a las ecuaciones de dinámica de fluidos. No descubriremos la estructura cuántica del espacio-tiempo de esta manera, y creemos que debido a esta década, los intentos de cuantificar la teoría de Einstein terminaron en un fuerte fracaso.

En cambio, debemos repensar la naturaleza de la gravedad y comprender lo que nos dice sobre la estructura microscópica del espacio-tiempo. El físico Ludwig Boltzmann utilizó este enfoque para comprender que los fenómenos de temperatura requieren la noción de materia como un grado discreto de libertad (en otras palabras, átomos). Boltzmann, de hecho, dijo que si algo puede estar caliente, debería contener grados microscópicos de libertad.

El espacio-tiempo también puede tener una temperatura y parecer caliente para ciertos observadores. Esta idea surgió gracias al trabajo de Jacob Beckenstein y Stephen Hawking en el contexto de los agujeros negros. Poco después, a mediados de los años 70, el trabajo de Bill Unrich y Paul Davis demostró que esta es la propiedad principal del espacio-tiempo. Al combinar el paradigma de Boltzmann con el hecho de que el espacio-tiempo, como la materia ordinaria, puede estar caliente, se llega a la conclusión de que el espacio-tiempo debe tener grados internos de libertad, como los átomos en la materia. La evidencia teórica en apoyo de esta conclusión ha comenzado a surgir en los últimos años [Padmanabhan, T. Los átomos del espacio-tiempo y la constante cosmológica. Journal of Physics: Conference Series 880, 012008 (2017)]. Esta observación contiene la clave para comprender la microestructura del espacio-tiempo, que rápidamente conduce a resultados notables.

En primer lugar, la evolución de un sitio de espacio-tiempo puede describirse en términos de grados de libertad (o, de manera equivalente, contenido de información) ubicado dentro de los límites de este sitio. En segundo lugar, la gravedad se vuelve insensible a los cambios a nivel de energía cero. En la teoría de Einstein, la gravedad es responsable de la cantidad absoluta de energía, por lo que es casi imposible calcular la constante cosmológica. Pero para un paradigma basado en el contenido de información, esto no es así. En tercer lugar, el enfoque informativo sugiere que no debemos imaginar la evolución cósmica de acuerdo con una cierta solución de las ecuaciones de Einstein. Estas ecuaciones surgen de un conjunto de ecuaciones más preciso que describe los grados cuánticos de libertad del espacio-tiempo [Padmanabhan, T. ¿Comprendemos realmente el cosmos? Comptes Rendus Physique 18, 275-291 (2017)].

El enfoque de información, confirmado por nuestro modelo de cosmina, nos da una imagen nueva y vívida del Universo, similar a un gran trozo de hielo que contiene una fuente de calor. Una fuente de calor derrite el hielo a su alrededor, creando una sección de agua que se expande, alcanzando el equilibrio termodinámico local. A gran escala, más cerca del límite de la fase, las moléculas aún no han alcanzado el equilibrio, ya que un trozo de hielo se calienta desde el interior. Curiosamente, esto es muy similar al comportamiento de nuestro universo. Una parcela de agua es similar al Universo observable (descrito por la teoría de Einstein). Está rodeado por una fase pregeométrica (similar al hielo), descrita hasta ahora por leyes desconocidas de la gravedad cuántica. La idea del Big Bang desaparece y, en cambio, aparece una transición de una fase a otra a lo largo de su frontera. La necesidad de un período inflacionario también desaparece.

Toda la plataforma es simple y elegante, ya que se describe mediante un único parámetro: la escala de energía de la transición de fase del Universo temprano de la pregeometría a la geometría de Einstein. Esto difiere de los modelos inflacionarios convencionales que contienen muchos parámetros y no tienen capacidades predictivas. Nuestro modelo no utiliza física no verificada. El único postulado que hicimos es que el contenido del Universo debería ser igual a 4π, ​​el área de superficie de una sola esfera.

El trabajo abre tres nuevas áreas de investigación. Primero, nos invita a estudiar la física de la fase pregeométrica en varios modelos de gravedad cuántica. En segundo lugar, brinda la oportunidad de estudiar la idea de información espacial utilizada en este trabajo e intentar conectarla con otras ideas similares utilizadas en otros contextos. Tercero, refuerza la idea de que el espacio-tiempo consiste en más grados elementales de libertad, al igual que la materia consiste en átomos, y nos anima a estudiar las diversas fases del espacio-tiempo de la misma manera que estudiamos las diversas fases de la materia en la física de la materia condensada .

Tanu Padmanabhan es profesor en el Centro Interuniversitario de Astronomía y Astrofísica de la India.