Cuando hablo con una persona lejos de la física sobre posibles dimensiones adicionales del espacio que desconocemos, entonces una de las preguntas más frecuentes es: “¿Cómo imaginas dimensiones adicionales? Solo puedo imaginar tres, y no entiendo cómo ir más allá; no tiene sentido para mí ".
Lo que los físicos no hacemos (al menos ninguno de mis conocidos ha afirmado estar haciendo esto), por lo que no imaginamos dimensiones adicionales. Mi cerebro es limitado como el tuyo, y aunque este cerebro crea fácilmente una imagen tridimensional del mundo en el que me puedo mover, no puedo obligarlo a representar una imagen de un mundo de cuatro o cinco dimensiones, como tú. Mi supervivencia no dependía de la capacidad de imaginar algo como esto, por lo que quizás no sea sorprendente que mi cerebro no esté sintonizado con esto.
En cambio, yo (y a juzgar por nuestro intercambio de ideas, la mayoría de mis colegas también) desarrollo la intuición basada en una combinación de analogías, trucos de visualización y cálculos. Aquí omitimos los cálculos, pero muchas analogías y trucos no son tan difíciles de explicar.
Las reflexiones sobre dimensiones adicionales se pueden aprender en dos etapas.
- Un paso simple es aprender a imaginar o describir el mundo con dimensiones adicionales. Ya conoce varias formas de hacerlo, incluso si no lo sabe, y puede aprender un poco más.
- La etapa más difícil es aprender cómo funciona todo en el mundo con dimensiones adicionales. Cómo trabajar con una aguja en cuatro dimensiones, y no en tres; si los planetas se moverán en órbitas alrededor del sol en seis dimensiones espaciales; se formarán protones y átomos? Aquí deberá aprender trucos desconocidos, que representan las diferencias entre un mundo con solo una o dos dimensiones y un mundo tridimensional que conocemos, y que funcionan por analogía.
Comencemos por ayudarlo a imaginar el mundo con dimensiones adicionales. Para hacer esto, debe pensar cómo en general representamos cualquier dimensión. Comencemos desde el principio.
- Un mundo con dimensiones cero es un punto. Poco se puede decir sobre él ahora, pero volveremos a él.
- El mundo unidimensional ya es bastante interesante.
- En mundos bidimensionales, están sucediendo cosas mucho más interesantes.
- Es importante evitar la confusión entre las dimensiones espaciales y el significado más general de la palabra "dimensión" en el lenguaje ordinario, así como en las matemáticas y las estadísticas.
- Y luego seguirán varios ejemplos de dimensiones adicionales, con énfasis en lo que significa exactamente "adicional", y cómo puede ser que en nuestro mundo haya dimensiones de las que no sabemos nada.
- También examinaremos cómo se pueden detectar exactamente estas mediciones invisibles.
Mundos unidimensionales
Un mundo con una dimensión espacial es mucho más simple que un mundo con tres, pero hay algo sobre lo que se puede razonar. Por ejemplo, hay varios tipos de mundos unidimensionales. No solo tienen ciertas propiedades comunes, sino también diferencias interesantes.
Para el primer ejemplo, consideremos la medición no como un concepto físico, sino como un concepto más general. Esto lo ayudará de muchas maneras, por ejemplo, distrayendo su intuición de conceptos erróneos naturales sobre qué dimensiones son y cómo funcionan. Hablemos de las ganancias anuales: cuánto dinero recibe una persona por un año determinado. Esta es una dimensión de estudio tan adecuada como todos los demás.
Medición de ingresos
Su ingreso del año pasado es un cierto número en su moneda local. Puede ser positivo o negativo, grande o pequeño; se puede representar como un punto en una línea, como en la fig. 1, que llamaremos el "punto de ingreso". Cada punto en la línea representa un posible retorno.
Fig. 1: una línea de ingresos de longitud infinita, cuyo lado izquierdo representa pérdidas, el lado derecho representa ingresos.Lo que hace que el ingreso anual sea una propiedad unidimensional es (muy aproximadamente) lo siguiente:
• La posición en el espacio está indicada por una unidad de información: en nuestro caso, por ingresos.
También tenga en cuenta que es continuo (o casi continuo): si dos personas tienen diferentes ingresos A y B, podemos encontrar un tercero cuyo ingreso esté entre A y B.
Estos dos hechos implican que los ingresos pueden cambiar continuamente a lo largo de la línea de ingresos, moviéndose hacia la derecha o hacia la izquierda, ya sea a ingresos más altos o más bajos. No hay otras opciones.
Por supuesto, la línea de ingresos no tiene nada que ver con el espacio físico en el que usted y yo podemos caminar, pero esto sigue siendo una dimensión. Y (al menos en principio) no tiene final en ninguna de las partes: (en principio) no hay límite en la cantidad de dinero que una persona puede ganar o perder en un año. Este mundo unidimensional no es tan diverso, pero aún podemos hacer algunas preguntas significativas al respecto:
- ¿Cómo se distribuyen los ingresos anuales en los Estados Unidos?
- ¿Cuál es el ingreso anual promedio en Japón?
- ¿Cómo cambian las respuestas a estas preguntas con el tiempo?
Estas preguntas tienen sentido en el mundo unidimensional de la línea de ingresos.
Medida del arcoiris
Y aquí hay otro mundo completamente diferente. Una sola dimensión está formada por los colores del arcoíris, desde el rojo, pasando por el naranja, hasta el amarillo, de allí al verde, [azul], azul y violeta [las personas de habla inglesa tienen seis colores en un arco iris, no emiten azul / aprox. transl.]. Desde este punto de vista, los colores forman un mundo unidimensional de tamaño finito. Fuera del rojo o púrpura, hay formas invisibles de flores, pero desde el punto de vista de sus ojos, la medición termina en ellas. Ahora se presenta no en forma de una línea infinita, sino en forma de segmento: la "línea del arco iris" en la Fig. 2. No lo confunda con la rueda de colores: si está cerrado, nuestra medición comienza con rojo y termina con púrpura. Y nuevamente, la posición en la línea del arco iris está determinada por una unidad de información (color), y es continua.
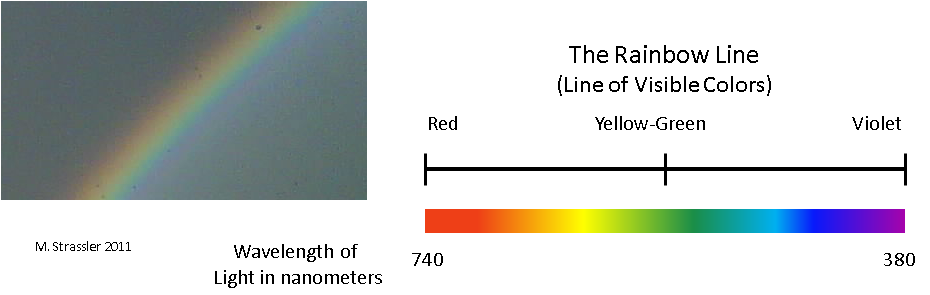Fig. 2¡Esto, obviamente, tampoco es una medida del espacio físico! Puedes lanzar una pelota desde tu casa a la casa de tu vecino, pero no puedes imaginar cómo lanzas una pelota de verde a naranja, no tiene sentido. Y aún así también será una dimensión. Aquí puede hacer muchas preguntas significativas: ¿cómo se mueve el color de la manzana a lo largo de la línea del arco iris en el proceso de convertir una manzana de verde a rojo? ¿Cuántos a la luz del sol de cada una de las flores? Si una estrella naranja comienza a ponerse roja, ¿se volverá amarilla primero?
Medición de la dirección del viento
Y aquí está la tercera opción de medición, y nuevamente otra. Si escucha el pronóstico del tiempo, se le informará que el viento pronto comenzará a soplar desde el norte, o desde el noroeste, o desde el suroeste. Las posibles direcciones del viento también son una medida. ¡Tenga en cuenta que esta no es una dimensión espacial! En esta dimensión, no puedes lanzar la pelota de la manera en que la lanzas hacia arriba, hacia la izquierda o hacia adelante. ¡Esta es una medida de direcciones en el espacio!
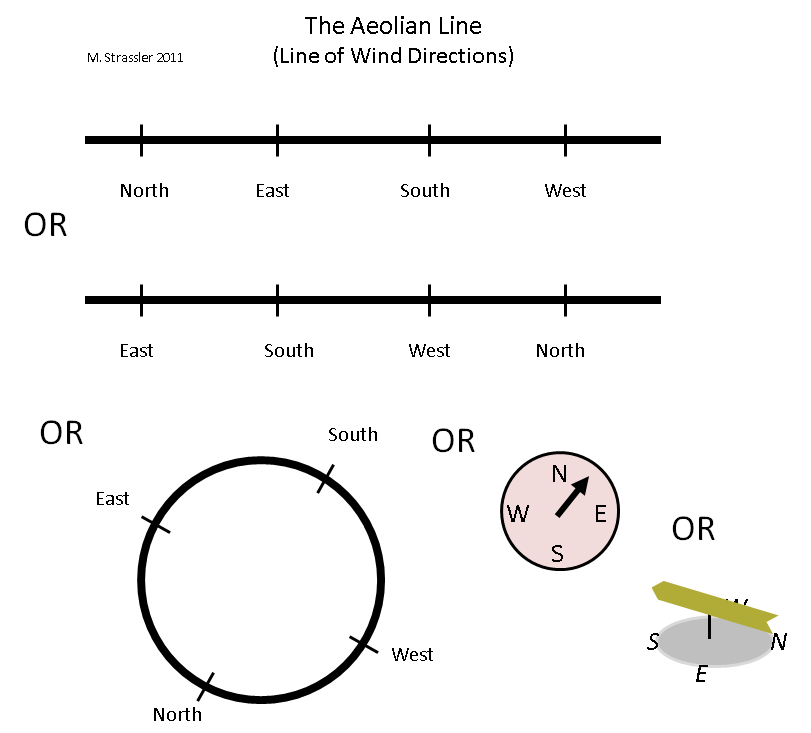Fig. 3¿Cómo se puede representar esta dimensión? Hay al menos dos métodos naturales para esto, como se muestra en la fig. 3. Uno usa el segmento - la "línea eólica" (
Aeolus es un semidiós, el gobernante de los elementos aéreos de los antiguos griegos) - pero la línea eólica difiere de la línea del arco iris en su frecuencia. La dirección del viento puede cambiar de norte a este, luego hacia el sur, luego hacia el oeste, y luego nuevamente hacia el norte, continuamente. Y en nuestra opinión, la línea se puede cortar en cualquier lugar: compare las dos líneas en la parte superior de la Fig. 3, que igualmente representan la línea eólica. La conclusión es que el viento puede ir desde el extremo derecho de la línea directamente al extremo izquierdo, y viceversa, por lo que no importa dónde cortarlo. O quizás la forma más fácil de representar esta línea periódica es en forma de círculo. ¡Eso es lo que estamos haciendo con una brújula o una veleta!
Tres mundos unidimensionales diferentes
Y aquí tienes mundos unidimensionales. ¡Mira cuán ricos son en detalles! Diferentes tamaños, diferentes propiedades. En la línea de ingresos, los ingresos pueden aumentar o disminuir para siempre. En la línea del arco iris, tus ojos solo pueden moverse a púrpura, o al revés, solo a rojo. Y en la línea eólica, el viento puede hacer un círculo completo tanto como desee, pero al mismo tiempo siempre volverá a una de las direcciones.
Estas variedades de mundos unidimensionales: infinito, finito y finito-periódico, representados por una línea, segmento y círculo infinitos, son los ingredientes básicos para comprender los mundos de dimensiones superiores. Me pondré en contacto con ellos más de una vez. En la fig. 4 se presentan, así como el cuarto tipo, que se extiende infinitamente en una sola dirección. Un ejemplo de tal medida puede ser la temperatura: puede ser arbitrariamente grande, pero hay la temperatura más baja posible, cero absoluto, por lo que la temperatura forma una línea que comienza en cero absoluto y sube desde allí, pero no baja.
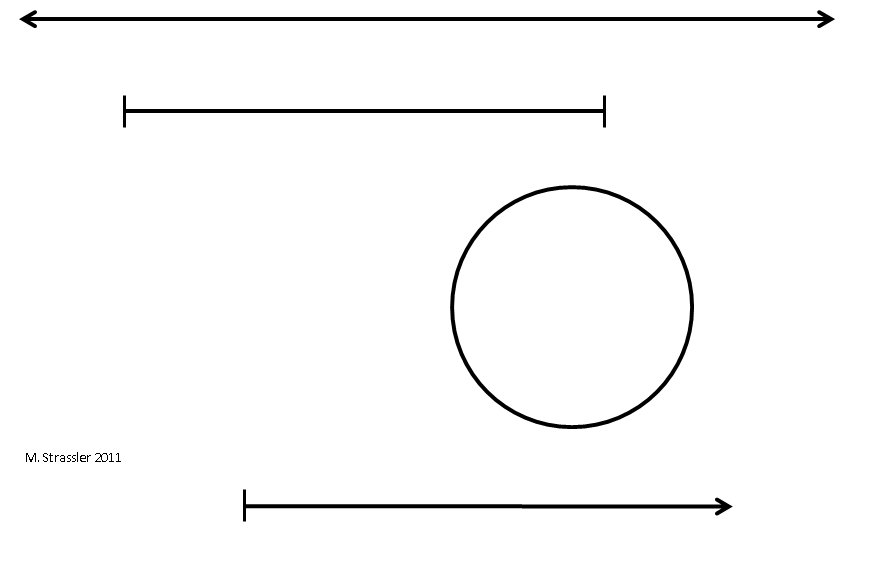Fig. 4 4Cómo representar dimensiones, espaciales y otras
Casualmente mencioné o usé varios métodos diferentes para representar mediciones. El ingreso puede ser representado por un número o una línea sin fin. El arco iris visible se puede representar como un segmento, o como un color, y también puede usar un número: la longitud de onda de los fotones correspondiente a un determinado color. La dirección del viento se puede representar mediante un círculo, o un segmento cuyo extremo izquierdo está conectado a la derecha, o palabras como norte, este, sur, oeste, o un número que define la dirección en grados, que va de 0 a 360 y vuelve a 0. Lo que podemos presentar una dimensión de muchas maneras diferentes nos brinda una tremenda flexibilidad para entrenar el trabajo intuitivo con dimensiones adicionales.
Para ilustrar este tipo de mediciones, elegí conceptos que no tienen nada que ver con el espacio físico (ingresos, color del arco iris, dirección del viento) para mostrar que las mediciones espaciales son ejemplos concretos de un concepto de medición más general. Comprender este hecho facilita enormemente los intentos de imaginar mundos con más de tres dimensiones. ¿Recuerdas que mencioné dos partes del proceso de pensamiento sobre dimensiones adicionales? Primero, aprende a representarlos; segundo, entender cómo funciona todo y cómo funciona en ellos. Las dimensiones espaciales tienen características asociadas con cómo funcionan algunas cosas en ellas, pero no con su presentación.
Mundos espaciales con una dimensión efectiva
Dado todo esto, consideremos los mundos espaciales que nos encontramos regularmente con una dimensión efectiva. O, más precisamente, situaciones en las que cierto aspecto de nuestro mundo se comporta como si el espacio tuviera una sola dimensión. Luego decimos que el mundo para ciertos participantes u objetos se vuelve efectivamente unidimensional.
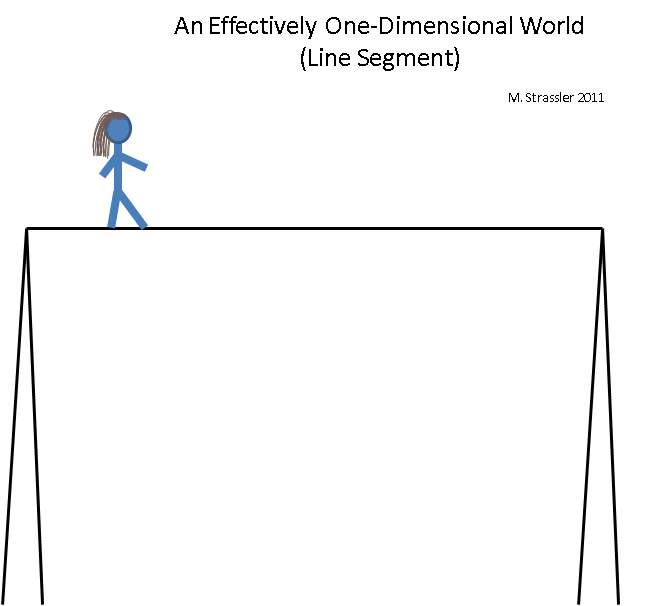Fig. 5 5Imagine un equilibrista equilibrado sobre una cuerda alta. El mundo del equilibrista es efectivamente unidimensional (aunque, por supuesto, en realidad sigue siendo tridimensional), ya que no puede moverse con seguridad en ninguna dirección que no sea de derecha a izquierda o de izquierda a derecha. Este mundo es como un mundo arcoíris: tiene una longitud finita, y cuando el equilibrista llega al final, necesita darse la vuelta y regresar (o salir de la cuerda, terminando una situación en la que el mundo se vuelve efectivamente unidimensional). ¿Qué más puedo decir? La posición en la cuerda se puede determinar mediante una unidad de información (por ejemplo, la distancia desde el poste izquierdo hasta el equilibrista). Dos caminantes de la cuerda floja pueden encontrarse en la misma línea, pero no cruzarse.
Podemos convertir el mundo de una cuerda en una línea eólica cerrándola en un círculo (Fig. 6). En él, dos caminantes de la cuerda floja tampoco podían cruzarse, esta es la propiedad principal de los mundos unidimensionales. Y esa seguiría siendo la dimensión final. Pero el equilibrista en tal situación ya podría caminar en un círculo continuo e interminable, sin detenerse.
Fig. 6 6Otros mundos unidimensionales conocidos (efectivamente):
- El camino angosto es un mundo unidimensional para automóviles;
- Un camino estrecho con un acantilado: para un turista que sube una montaña;
- Los pisos de un edificio alto son para un ascensor.
En general, el mundo sigue siendo tridimensional, pero para describir un automóvil, un turista o un elevador, solo se necesita representar una dimensión.
En el futuro, recuerde: vivimos en un aparente mundo tridimensional, y todo lo que encontramos nos parece tridimensional. Pero a veces nuestro mundo tridimensional (más precisamente, parte de él) puede comportarse tan efectivamente unidimensional o bidimensional (¿puede encontrar ejemplos?) ¡O incluso cero-dimensional! (¡Todos los que tienen mala suerte de quedar atrapados en un atasco de tráfico que no se mueve a ningún lado saben lo que es este mundo con cero dimensiones!) Esta intuición nos será muy útil más adelante.