Un destacado matemático ha revelado los detalles de cómo sus éxitos en el estudio de problemas matemáticos milenarios están relacionados con conceptos tomados de la física.
Kim MignonLas matemáticas están llenas de sistemas de números raros de los que la mayoría de la gente nunca ha oído hablar. Algunos de ellos incluso serán difíciles de imaginar. Pero
los números racionales son familiares para todos. Estos son números para contar objetos y fracciones, todos los números que conocemos de la escuela primaria. Pero en matemáticas, a veces las cosas más simples son las más difíciles de entender. Son simples, como una pared lisa, sin grietas ni protuberancias, u otras propiedades obvias a las que se pueda agarrar.
Minion Kim , matemático de la Universidad de Oxford, está particularmente interesado en la cuestión de qué números racionales son adecuados para resolver ecuaciones de cierto tipo. Este problema ha estimulado a los especialistas en teoría de números durante milenios. Y apenas lograron avanzar hacia su solución. Cuando una pregunta se ha estudiado durante tanto tiempo y sin respuesta, se puede concluir que la única forma de avanzar en ella es presentar una idea radicalmente nueva. Esto es exactamente lo que hizo Kim.
“No existe mucha tecnología, aunque hemos estado trabajando en esto durante los últimos 3000 años. Entonces, cuando alguien presenta una forma verdaderamente nueva de hacer esto, es de gran interés, y Mignon hizo exactamente eso ”, dijo Jordan Ellenberg, matemático de la Universidad de Wisconsin en Madison.
En la última década, Kim ha descrito una forma completamente nueva de encontrar patrones en el mundo aparentemente desordenado de los números racionales. Describió este método en artículos y en conferencias, y lo transmitió a los estudiantes que ahora continúan este trabajo por su cuenta. Pero él siempre guardaba algo. Su visión, que dio vida a sus ideas, se basó no en un mundo puro de números, sino en conceptos tomados de la física. Para Kim, las decisiones racionales recuerdan de alguna manera la trayectoria de la luz.
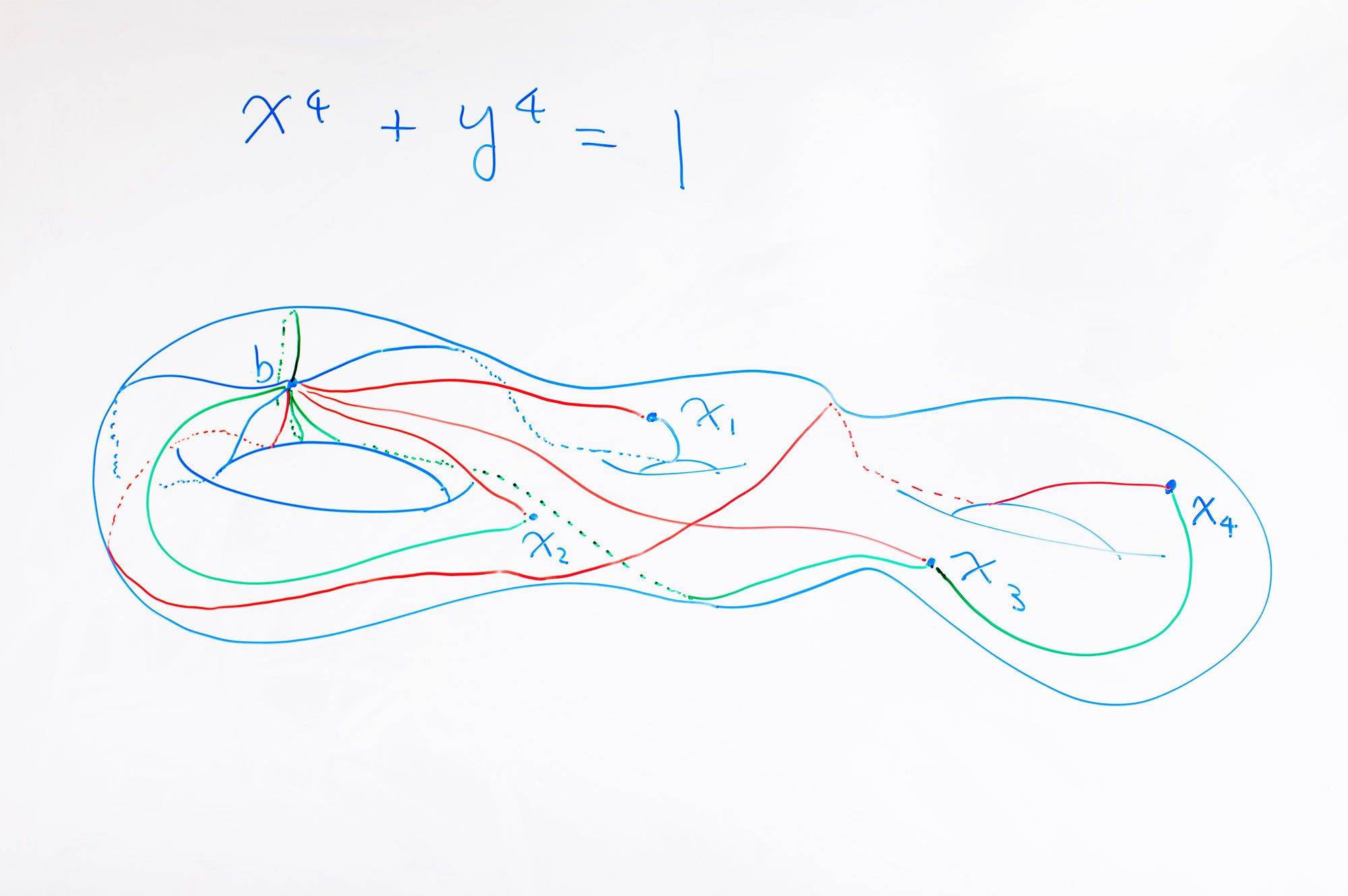Un objeto matemático, un toro de tres agujeros, adorna el tablero de Kim en la Universidad de Oxford.Si esta conexión parece fantástica, entonces lo es, incluso para los matemáticos. Por lo tanto, Kim no reveló sus detalles durante mucho tiempo. "Lo escondí porque durante muchos años estaba confundido por la conexión con la física", dice. "Los especialistas en teoría de números son personas muy prácticas, y la influencia de la física a veces los hace escépticos de las matemáticas".
Pero ahora Kim dice que está listo para compartir su visión. "¡Creo que el cambio es solo un síntoma del envejecimiento!" - escribió Kim, quien cumplió 53 años, en una de las primeras cartas que intercambiamos para escribir esta historia.
Recientemente celebró una conferencia que reunió a expertos en teoría de números y teoría de cuerdas. También esbozó borradores de artículos que comenzaban a describir su inspiración para la comunidad matemática, no acostumbrado a pensar en números usando analogías directas con el mundo físico.
Solo queda un obstáculo: la última parte de la analogía de la física en las matemáticas, que Kim aún no ha resuelto. Espera que al invitar a otros a compartir su visión, especialmente a los físicos, reciba la ayuda necesaria para completar el trabajo.
Acertijo antiguo
Las soluciones racionales de ecuaciones atraen activamente la mente humana. Traen satisfacción, similar a lo que obtienes de las piezas del rompecabezas que encajan en su lugar. Por lo tanto, son los héroes de las hipótesis matemáticas más famosas.
Los números racionales incluyen enteros y cualquier número que pueda expresarse como la razón de dos enteros, por ejemplo, 1, -4 o 99/100. Los matemáticos están especialmente interesados en los números racionales que resuelven ecuaciones diofantinas: ecuaciones polinómicas con coeficientes enteros, por ejemplo, x
2 + y
2 = 1. Reciben su nombre del matemático
Diophantus , que los estudió en Alejandría en el siglo III d.C.
Las soluciones racionales son difíciles de encontrar en el caso general, ya que no obedecen a ninguna regularidad geométrica. Tome la ecuación x
2 + y
2 = 1. Sus soluciones en
números reales forman un círculo. Elimine todos los puntos del círculo que no puedan expresarse como fracciones, y solo quedarán decisiones racionales que no formen un objeto tan ordenado. Las soluciones racionales se ven dispersas al azar alrededor de la circunferencia.
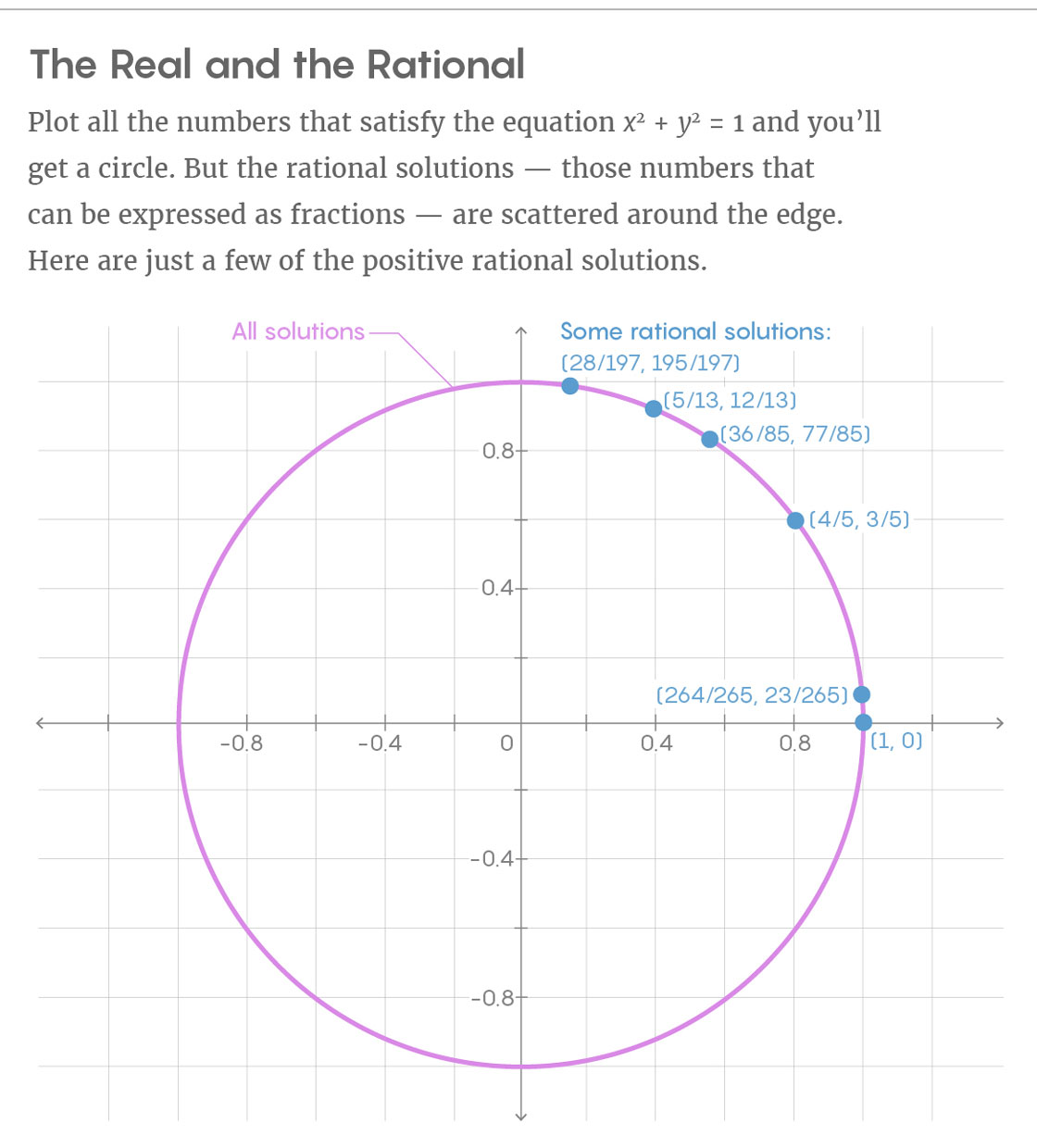
“La condición a la que debe obedecer el punto para tener coordenadas racionales no es en absoluto geométrica. Es imposible escribir una ecuación que los puntos racionales deben satisfacer ", dice Kim.
A menudo es bastante simple encontrar una solución racional, o incluso varias. Pero los matemáticos a quienes no les gusta la subestimación están más interesados en encontrar todas las soluciones racionales. Y esto es mucho más complicado. Es tan difícil que la evidencia de incluso una declaración menor sobre el número de decisiones racionales es suficiente para aprobar una luminaria matemática. En 1986,
Gerd Falting ganó el
Premio Fields , el premio matemático más alto, principalmente por probar
la hipótesis de Mordell , que dice que ciertas clases de ecuaciones diofantinas tienen solo un número finito de soluciones racionales.
La prueba de Falting fue un punto de inflexión en la teoría de números. Y también por lo que los matemáticos llaman "prueba ineficaz", porque no dio el número exacto de soluciones racionales y no las encontró. Desde entonces, los matemáticos han estado buscando formas de realizar estos próximos pasos. Los puntos racionales parecen aleatorios en un gráfico de ecuación regular. Los matemáticos esperan que al cambiar el contexto dentro del cual reflexionan sobre un problema, estos puntos puedan parecer una combinación significativa que pueda describirse de alguna manera exacta. El problema es que las áreas bien conocidas de las matemáticas no proporcionan ese contexto.
Kim en su oficina en Oxford"Para obtener resultados efectivos desde puntos racionales, claramente existe la necesidad de una nueva idea", dijo Ellenberg.
Ahora hay dos supuestos principales sobre la naturaleza de tal idea. Uno proviene del matemático japonés
Shinichi Motizuki , quien publicó en 2012 un
trabajo matemático complejo e innovador de varios cientos de páginas en la página de su facultad en la Universidad de Kyoto. Cinco años después, este trabajo sigue siendo en gran medida incomprensible. Otra idea nueva surgió de Kim, que trató de imaginar números racionales en un contexto numérico extendido en el que sus patrones ocultos comienzan a aparecer.
Solución simétrica
Los matemáticos a menudo dicen que cuanto más simétrico es un objeto, más fácil es estudiarlo. Por lo tanto, les gustaría ubicar el estudio de las ecuaciones de diofantina en condiciones que contengan más simetría que aquellas en las que este problema surge naturalmente. Si esto tiene éxito, podrán usar las nuevas simetrías para rastrear los puntos racionales que necesitan.
Para comprender cómo la simetría ayuda a un matemático a navegar un problema, imagine un círculo. Quizás su objetivo es identificar todos los puntos en el círculo. La simetría ayuda mucho, porque crea un mapa que te permite moverte desde los puntos que conoces hasta aquellos que aún no se han descubierto.
Imagine que ha encontrado todos los puntos racionales en la parte inferior de un círculo. Como el círculo tiene simetría de espejo, los puntos pueden reflejarse hacia arriba (cambiando los signos en todas las coordenadas y) y de repente obtener todos los puntos desde la parte superior. El círculo en general tiene una simetría tan rica que para buscar todos los puntos en él, necesita encontrar la posición de un solo punto y luego combinarlo con el conocimiento sobre la simetría del círculo: solo necesita aplicar la simetría rotacional infinita del círculo al punto de partida.
Pero si el objeto geométrico con el que trabaja es mucho menos correcto, como, por ejemplo, un camino que se mueve aleatoriamente, tendrá que trabajar mucho para determinar cada punto por separado; no tendrá relaciones simétricas que le permitan marcar puntos desconocidos cuando Ayuda famosa.
Los conjuntos numéricos también pueden tener simetrías, y cuantas más simetrías hay en un conjunto, más fácil es de entender: puede aplicar relaciones simétricas para detectar valores desconocidos. Los números con ciertos tipos de simetría forman un "grupo", y los matemáticos usan las propiedades del grupo para comprender los números que contiene.
Muchas soluciones racionales de la ecuación no tienen que tener simetría y no forman un grupo, razón por la cual los matemáticos se enfrentan a una tarea poco realista al tratar de encontrar soluciones de una en una.
A partir de la década de 1940, los matemáticos comenzaron a estudiar métodos para organizar ecuaciones de diofantina en condiciones más simétricas. El matemático Claude Chabauty descubrió que dentro del espacio geométrico más grande que creó (usando un universo extendido de números llamados números
p-adic ), los números racionales forman su propio subespacio simétrico. Tomó este subespacio y lo
combinó con un diagrama de la ecuación de Diophantine. Los puntos de su intersección resultaron ser soluciones racionales de la ecuación.
En la década de 1980, el matemático
Robert Coleman especificó el trabajo de Chaboti. Durante las siguientes dos décadas, el enfoque de Coleman-Chaboti fue la mejor herramienta matemática que los matemáticos tuvieron para encontrar soluciones racionales a las ecuaciones de Diophantine. Pero solo funciona si la gráfica de la ecuación se correlaciona con el tamaño de un espacio más grande en cierta proporción. Cuando se rompe, se hace difícil encontrar con precisión la posición de los puntos de intersección de la curva de ecuación y los números racionales.
"Si su curva está en un entorno donde hay demasiados puntos racionales, comienzan a acumularse y es difícil distinguir cuáles están en la curva", dijo Kiran Kedlaya, matemático de la Universidad de California en San Diego.
Y luego entra Kim. Para expandir el trabajo de Chaboti, quería encontrar un espacio aún más grande para estudiar las ecuaciones de Diophantine, un espacio donde los números racionales están más fragmentados, lo que nos permite estudiar los puntos de intersección con una gran cantidad de variedades de ecuaciones de Diophantine.
Espacios de espacios
Si necesita un espacio más grande y algunos consejos sobre cómo puede usar la simetría para orientarse en él, la física le conviene.
En el caso general, el espacio en el sentido matemático es cualquier conjunto de puntos con una estructura geométrica o topológica. Mil puntos dispersos por voluntad o no, no forman espacio, no están conectados entre sí por una estructura. Pero la esfera, que es una organización conectada de puntos, ya es espacio. Como un toro, o un plano bidimensional, o un espacio-tiempo cuatridimensional, donde vivimos.
Además de estos, hay espacios aún más exóticos que se pueden imaginar como "espacios de espacios". El ejemplo más simple: digamos que tienes un triángulo, y este es el espacio. Ahora imagine el espacio de todos los triángulos posibles. Cada punto en él representa un cierto triángulo, y las coordenadas de este punto están determinadas por los ángulos del triángulo representado por él.
Tal idea es a menudo útil en física. Dentro del marco de la teoría general de la relatividad, el espacio y el tiempo evolucionan constantemente, y los físicos consideran cada configuración de espacio y tiempo como un punto en el espacio de todas las configuraciones espacio-temporales. También aparecen espacios de espacios en el área que los físicos llaman invariancia de calibre, trabajando con campos superpuestos en el espacio físico. Estos campos describen cómo cambian las fuerzas como el electromagnetismo y la gravedad al moverse en el espacio. Uno puede imaginar que en cada punto del espacio la configuración de estos campos es ligeramente diferente, y que todas estas configuraciones diferentes forman puntos en el "espacio de todos los campos" de mayor dimensión.
Este espacio de campos de la física es una analogía cercana a la propuesta de Kim para la teoría de números. Para entender esto, imagine un rayo de luz. Los físicos representan la luz que se mueve a través del espacio de los campos de mayor dimensión. En este espacio, la luz seguirá un camino que se adhiere al principio de menor resistencia y minimiza la cantidad de tiempo requerido para llegar del punto A al punto B. Este principio explica por qué la luz se dobla cuando se mueve de un material a otro: un camino curvo minimiza el tiempo costos.
Los espacios más grandes de espacios que aparecen en física tienen simetrías adicionales que no están presentes en ninguno de los espacios que representan. Estas simetrías llaman la atención sobre ciertos puntos, por ejemplo, enfocándose en un camino que minimiza el tiempo. Las mismas simetrías, construidas de manera diferente y en un contexto diferente, pueden enfatizarse en otros puntos, por ejemplo, en puntos correspondientes a soluciones racionales de ecuaciones.
Conectando la simetría con la física
En teoría de números, no hay partículas que puedan rastrearse, pero tiene algo así como espacio-tiempo, y ofrece una manera de dibujar caminos y crear el espacio de todos los caminos posibles. A partir de esta correspondencia básica, Kim desarrolla esquemas en los que "el problema de encontrar la trayectoria de la luz y encontrar soluciones racionales de ecuaciones diofantinas son dos caras del mismo problema", como explicó en una conferencia de física matemática en Heidelberg la semana pasada.
Las soluciones de las ecuaciones de Diofantina forman espacios: estas son curvas definidas por ecuaciones. Estas curvas pueden ser unidimensionales, como un círculo, o multidimensionales. Por ejemplo, si construyes una solución compleja de la ecuación diofantina x
4 + y
4 = 1, obtienes un toro con tres agujeros. Los puntos racionales en dicho toro no tienen una estructura geométrica, por eso es difícil encontrarlos, pero se pueden comparar con puntos en un espacio multidimensional de espacios que poseen dicha estructura.
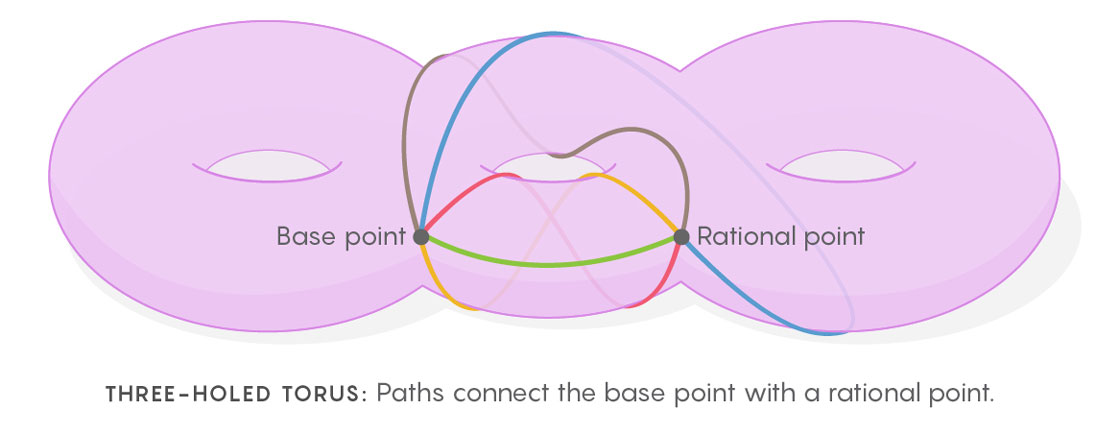
Kim crea este espacio multidimensional de espacios, imaginando las formas en que se pueden dibujar curvas cerradas en el toro (o en el espacio que define la ecuación). El procedimiento para dibujar curvas se ve así. Primero debe seleccionar el punto de partida, luego dibujar un bucle desde este punto a cualquier otro, y volver al primero. Ahora repita este proceso, dibujando los caminos que conectan el punto base con todos los otros puntos del toro. Obtendrá la espesura de todos los bucles posibles que comienzan y terminan en el punto base. Este conjunto de bucles es un objeto centralmente importante de las matemáticas llamado
grupo fundamental del espacio.
Cualquier punto en el toro puede usarse como punto de partida. Cada punto tendrá un matorral único de caminos que emanan de él. Cada una de estas colecciones de rutas se puede representar como un punto en un "espacio multidimensional de todos los conjuntos de rutas" (como el espacio de todos los triángulos posibles). Este espacio de espacios es geométricamente muy similar a lo que los físicos construyen en la teoría de la invariancia de indicadores: la forma en que cambian los conjuntos de caminos cuando vas de un punto en un toro a otro es muy similar a cómo cambian los campos cuando vas de un punto a otro. otro en espacio real. Este espacio de espacios tiene simetrías adicionales que no están en el toro mismo. Y aunque los puntos racionales en un toro no tienen simetría, si vamos al espacio de todos los conjuntos de caminos, podemos encontrar simetrías entre puntos asociados con números racionales. Obtiene simetrías que antes no eran visibles.
"A veces digo que la" simetría aritmética oculta "está codificada en estos caminos, que es muy similar a las simetrías internas de la teoría de la invariancia de indicadores", dijo Kim.
Al igual que Chaboti, Kim encuentra soluciones racionales al explorar los puntos de intersección en el espacio más grande que crearon. Utiliza las simetrías de este espacio para llegar a los puntos de intersección. Espera desarrollar una ecuación que defina con precisión estos puntos.
En el contexto físico, uno puede imaginar todas las formas posibles en que puede ir un rayo de luz. Este es su "espacio de todos los caminos". Los físicos están interesados en los puntos en este espacio que corresponden a caminos que minimizan el tiempo. Kim cree que los puntos correspondientes a los matorrales de caminos que emanan de puntos racionales tienen algo parecido a la misma propiedad, es decir, estos puntos minimizan algunas propiedades que ocurren cuando se consideran las formas geométricas de las ecuaciones de Diophantine. Él todavía no ha descubierto cuál podría ser esta propiedad.
"Lo que empecé a tratar de encontrar" es el principio de menor resistencia en un contexto matemático, me escribió en una carta. "Todavía no lo he encontrado, pero estoy seguro de que existe".
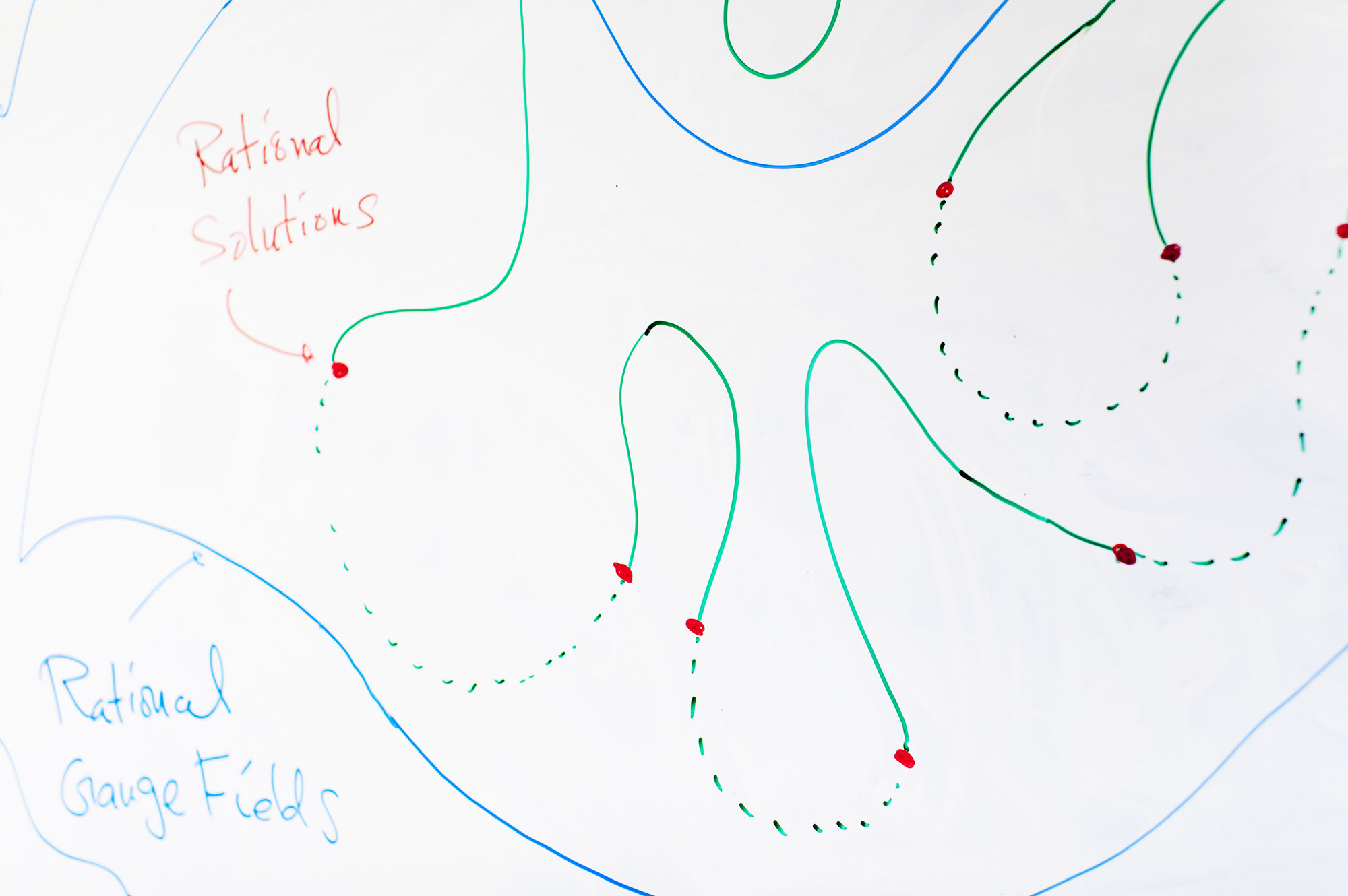
Futuro incierto
En los últimos meses, describí la visión de Kim, inspirada en la física, por varios matemáticos, admiradores de sus contribuciones a la teoría de números. Pero al enterarse de tal detalle de su trabajo, se perdieron.
"Como teórico de las cantidades representativas, si me mostraran todos esos logros asombrosos realizados por el Minion y preguntara si se inspiraron en la física, diría: ¿De qué demonios estás hablando?" - dijo Ellenberg
Hasta ahora, Kim no ha mencionado la física en ninguno de sus trabajos. En cambio, escribe sobre objetos llamados "variaciones de Selmer" y examina la relación entre las variaciones de Selmer en el espacio de todas las variaciones de Selmer. Tales cosas son familiares para los expertos en teoría de números. Pero para Kim, siempre fueron solo otra designación de ciertos objetos físicos."Debería haber una manera de usar ideas físicas para resolver problemas en la teoría de números, pero aún no hemos pensado lo suficiente como crear una plataforma así", dijo Kim. "Estamos en un estado en el que nuestra comprensión de la física está bastante desarrollada, y muchos especialistas en teoría de números están interesados en ella para dar el siguiente paso".El principal obstáculo para el método Kim es encontrar alguna acción para minimizar el espacio de todos los conjuntos de bucles. En el mundo físico, este enfoque parece natural, pero en aritmética no tiene un significado obvio. Incluso los matemáticos que vigilan de cerca el trabajo de Kim no están seguros de si puede encontrarlo.“Creo que el programa de Kim hará muchas cosas maravillosas por nosotros. "No creo que tengamos tan claro como Mignon quiere entender si los puntos racionales son soluciones clásicas para la teoría de la medición aritmética", dijo Arnav Tripathy, profesor de física matemática en la Universidad de Harvard.Hoy, el lenguaje de la física casi no se cruza con la práctica de la teoría de números. Kim cree que esto seguramente cambiará. Hace cuarenta años, la física, la geometría y la topología tenían poco en común. Luego, en la década de 1980, varios matemáticos y físicos, ahora cifras significativas, encontraron formas exactas de usar la física para estudiar las propiedades de las formas. Después de este desarrollo, esta área cambió y no volvió a los métodos anteriores.“Hoy en día es prácticamente imposible estar interesado en la geometría y la topología sin saber nada de física. Estoy bastante seguro de que esto sucederá también con la teoría de números "en los próximos 15 años, dijo Kim. "Todas las conexiones son extremadamente naturales".