Ya les he
dado algunos ejemplos de cómo se pueden representar
dimensiones adicionales en la naturaleza, dimensiones en el espacio, de las cuales ni siquiera somos conscientes. Pero hasta ahora aún no he explicado cómo los científicos pueden aprender sobre su existencia.
Aquí puede usar varias estrategias básicas, pero por ahora me concentraré en una simple consecuencia de la existencia de dimensiones adicionales. Tiene un carácter muy general y conduce a una estrategia para estudiar la física de partículas, que es relevante para muchos estudios, incluidos los experimentos en el Gran Colisionador de Hadrones.
Mi explicación irá en dos etapas. En la primera etapa, usando la física más simple, te daré una comprensión intuitiva, simple pero imperfecta (ya que no se tendrá en cuenta la mecánica cuántica), y proporcionaré una respuesta parcialmente incorrecta. En el segundo paso, corregiré la inexactitud, lo que requerirá otra complicación adicional, y luego verá la respuesta completa.
Pero antes de comenzar la explicación, primero te daré una respuesta de inmediato para que entiendas lo que necesitaré explicarte. Aquí está, de varias maneras, para aclararlo.
Cualquier partícula que se mueva en dimensiones adicionales a las que ya conocemos parecerá usted y yo, observadores ingenuos que no tienen idea de dimensiones adicionales, a partículas de varios tipos, cada una de las cuales se mueve solo en dimensiones conocidas por nosotros, y las diferencias entre las cuales muy pequeño, excepto por sus masas.
En otras palabras: si una partícula de cierto tipo puede moverse en todas las dimensiones, a un observador desinformado le parecerá que en la naturaleza no solo existe esta partícula (que se mueve solo en las dimensiones que conoce), sino un conjunto completo de partículas relacionadas, "socios KK", cada uno que también se mueve en direcciones conocidas, ligeramente diferentes de la partícula original, excepto que serán más pesadas. "KK" se refiere a la
teoría de Kaluza-Klein , sobre la cual más tarde.
Supongamos que vivimos en cuatro dimensiones espaciales, tres de las cuales son grandes (que conocemos), y la cuarta es muy corta (como el ancho de la tira que utilicé en los ejemplos anteriores). Por corto se entiende una distancia realmente corta, menor que el diámetro del protón. Llame a esta distancia L.
Ahora imagine que hay una partícula, muy, muy pequeña, más pequeña que L, que puede moverse libremente en las cuatro dimensiones espaciales. También asumimos la existencia de observadores astutos que saben que esta partícula puede moverse en cuatro dimensiones y tiene una masa m. Ahora consideraremos observadores ingenuos que no conocen la pequeña dimensión espacial, que creen que viven en un mundo tridimensional. Después de algunos experimentos indicados en la fig. 1, podemos decir: “aquí hay un tipo de partícula que puede moverse en tres dimensiones, y tiene una masa m; pero, mira, otro tipo de partícula, también capaz de moverse en tres dimensiones, y es similar a la primera, solo su masa M, mucho más que m; y, wow, aquí hay otro tipo de partícula capaz de moverse en tres dimensiones, similar a la primera, solo que tiene una masa M ', mayor que M; y otro tipo de partícula, masa M ”; y más y más ... "
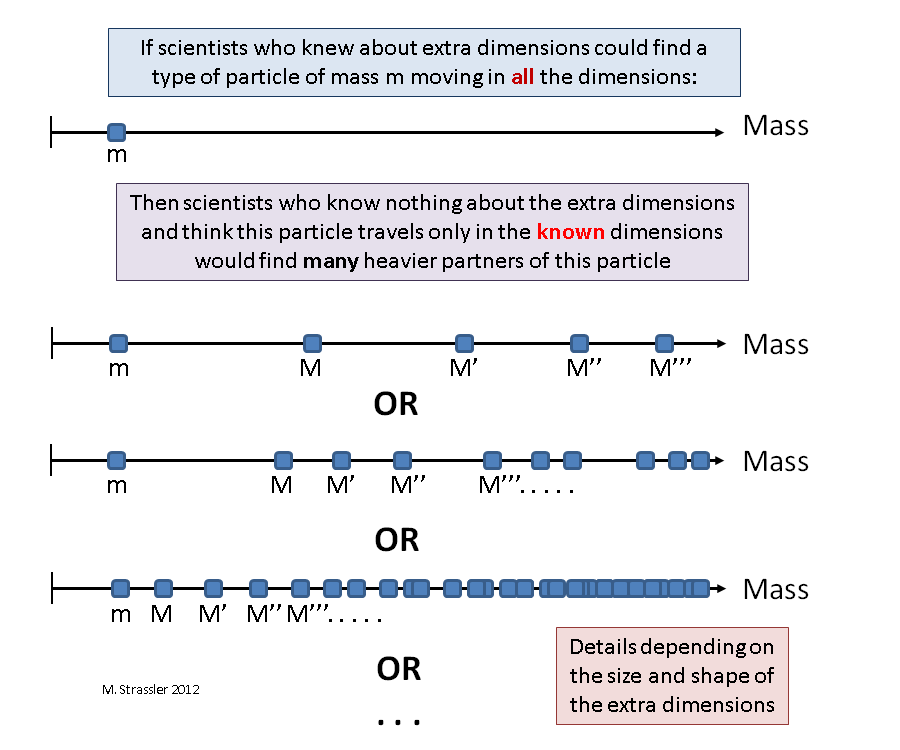 Fig. 1
Fig. 1Las masas M, M ', M ”y así sucesivamente están determinadas por la combinación de la masa fundamental m y la geometría de las dimensiones espaciales adicionales, en particular, M, M', M”, etc., son inversamente proporcionales a L. Cuanto menor es L, mayor M, M ', M ”y así sucesivamente, y lo más difícil es encontrar socios de control de calidad pesados. Además, la secuencia de masas que aparece en los socios de CC proporciona una indicación directa de la cantidad, el tamaño y la forma de las mediciones adicionales. Puede dar una analogía musical: este hecho se debe al hecho de que los armónicos exactos producidos por el instrumento pueden proporcionar información sobre su forma y tamaño.
Por ejemplo: si los fotones (partículas de luz) pudieran moverse en una o varias dimensiones adicionales, como un bote en un canal, entonces un observador que estaría al tanto de las dimensiones adicionales las describiría como partículas sin masa (m = 0) que se mueven en todas las dimensiones . Pero un científico humano que hasta ahora solo conoce un fotón sin masa que se mueve en tres dimensiones conocidas descubriría un conjunto de partículas pesadas similares a los fotones. Cuanto más pequeño sea el tamaño de la medición adicional, mayor será la masa de fotones KK y más difícil será abrirlos; más precisamente, cuanto más pesados sean, y más energía necesitará el acelerador de partículas para generarlos.
Es muy posible que varios tipos de partículas puedan moverse en dimensiones adicionales, y en este caso, los científicos descubrirán socios KK pesados para cada uno de estos tipos de partículas (ver Fig. 2). El descubrimiento de un pequeño número de partículas pesadas que se asemejan a algunas de las partículas ligeras conocidas, cuya distribución de masa demostrará similar a la Fig. La distribución 2 indicará claramente que las nuevas partículas son socios de CC y que tenemos una o más dimensiones adicionales.
 Fig. 2
Fig. 2Esta es la respuesta simple: una partícula que se mueve tanto en dimensiones adicionales como en las conocidas se nos abrirá a través del descubrimiento de sus pesados socios de control de calidad. Más adelante describiré con mayor precisión cómo puede intentar producir y abrir socios de control de calidad en el experimento. En los
siguientes artículos, describiré por qué esta respuesta en particular será correcta, y daré una versión simple y compleja de la explicación.