Asociación Kaluza-Klein partners, parte 2

En un artículo anterior, expliqué por qué a los observadores ingenuos que no saben acerca de la presencia de una dimensión adicional les parece que una partícula que puede moverse en dimensiones adicionales tiene socios de Kaluza-Klein (KK), versiones más pesadas de la partícula original. Señalé que cuando la partícula inicial de masa m se mueve en la dirección de la dimensión adicional, le parece al observador ingenuo inmóvil y más pesado de lo que debería ser, es decir, como si fuera una partícula de un tipo diferente. Esta clase de partículas supuestamente nuevas, similar a la original, pero más pesada, se llama socios de control de calidad.

En el caso de una tira , si una partícula de masa m se mueve a través de la tira con un momento p, el observador que considere la tira como una línea asumirá que la partícula es un compañero KK con momento cero y masa M,

$$

$$M ^ 2 = m ^ 2 + (p_ {across} / c) ^ 2> m ^ 2$$

Aunque esto es generalmente cierto, se deduce que para cada masa M mayor que m, debe haber su propio socio de CC. Pero esto no es así: nuestro mundo es cuántico (ver Fig. 1 del artículo anterior). Ahora descubrimos exactamente cómo la mecánica cuántica cambia la imagen completa.

La característica clave de la física cuántica que necesitamos es que para una "partícula" cuántica que se mueve en una medida de tamaño finito, no todos los valores posibles de p a _{través son} permisibles. En una formulación más general: la mecánica cuántica sugiere que una "partícula" que se mueve en una medida de tamaño finito solo puede tener ciertos valores de momento en esta dirección.

¡Esta es una de las consecuencias más importantes y extrañas de la mecánica cuántica! A primera vista, esto es completamente contraintuitivo, ya que ¿qué puede evitar que le pidas a la "partícula" con el impulso p una ligera aceleración para que su impulso sea ligeramente diferente de p?

¿Qué es un cuanto?

Es posible que haya notado que comencé a citar la palabra "partícula", porque en el contexto actual necesitamos distinguir el término "partícula", usado para describir electrones, muones, quarks, gluones y todas las demás partículas elementales conocidas, desde un concepto intuitivo partículas que heredamos de nuestra experiencia con polvo, arena, sal y grava. Sería mejor llamar a tales "partículas" como un electrón, fotón, Quark, etc., cuantos, objetos más astutos. Estos cuantos son perturbaciones de los campos; se parecen mucho más a las olas que a las partículas. La mejor manera de entender cuántica es imaginar ondas. Este es otro punto lingüístico importante: cuando digo "ola", no me refiero a algo como una ola separada en el océano rompiendo en la orilla, me refiero a una secuencia de olas con muchas crestas y valles.

Un ejemplo de tales ondas serán las ondas electromagnéticas, que también incluyen ondas de luz, distinguibles para nuestros ojos. Imagine que tomamos tal onda, por ejemplo, luz láser, y atenuamos la luz cada vez más. ¿Cómo se puede amortiguar? Resulta que en nuestro mundo cuántico existe el menor destello de luz posible que llamamos un cuántico de luz, o un fotón. Un fotón es una onda de luz cuya altura e intensidad de onda es la más pequeña posible. Todos estos conceptos y nombres se los debemos a Einstein, quien, a pesar de su conocida insatisfacción con las consecuencias conceptuales de la mecánica cuántica, fue uno de los fundadores de esta teoría.

No hay nada intuitivo, desde mi punto de vista, que las ondas de luz estén compuestas de cuantos, ya que esto no se manifiesta en ninguno de los procesos que observamos directamente. Pero nuestros cuerpos, gracias a procesos que no conocemos, usan este hecho constantemente. La luz de la lámpara parece continua para nuestro cerebro, pero nuestros ojos realmente absorben los fotones de uno en uno. Además, vi con mis propios ojos la confirmación de que la luz consiste en cuantos - sé de esto no solo de los libros.

Los físicos a menudo llamamos a estos cuantos de luz "partículas de luz", porque en muchos sentidos se comportan como partículas. Cualquier fotón que se mueve en línea recta por sí mismo tiene cierta energía e impulso; todos los fotones tienen el mismo valor de masa (específicamente, cero); un fotón no puede dividirse en partes más pequeñas; un fotón solo puede ser emitido o absorbido en su totalidad. Estas propiedades corresponden aproximadamente a lo que nuestra intuición podría esperar de partículas como granos de arena, bolas de vidrio, partículas de polvo, etc.

Pero la palabra "cuántico" por muchas razones es mejor que la palabra "partícula", ya que algunas propiedades de los cuantos son similares a las propiedades de las partículas, y algunas a las propiedades de las ondas. Un ejemplo bien conocido del comportamiento de las olas es una forma cuántica de atravesar dos puertas simultáneamente e interactuar (en el mismo sentido que las olas interactúan entre sí y las crestas con canales se destruyen mutuamente). Y luego veremos otro ejemplo.

Debe recordarse que lo que se hace para el fotón también se hace para todas las "partículas" conocidas. De hecho, cada uno de ellos es un tipo de cuanto: las ondas de la altura más baja posible en el campo correspondiente. Un electrón es un cuanto de un campo electrónico. Quark es un cuanto de un campo de quark. La partícula Z es el cuanto del campo Z, y así sucesivamente.

Quantums - socios de control de calidad

Es hora de descubrir lo que prometí explicarte: por qué la naturaleza ondulatoria de los cuantos implica que las masas de partículas de los socios de KK toman valores definidos, y no todos los valores posibles, grandes masas m de la "partícula" original. El famoso físico Louis de Broglie , siguiendo los rastros de las primeras ideas de Einstein, definió claramente por primera vez que la relación entre ondas, partículas y cuantos implica que para un cuanto existe una relación entre:
• Su impulso (una propiedad que se asemeja a las propiedades de las partículas),
• Y su longitud de onda (una propiedad que se asemeja a las propiedades de las ondas) [y nuevamente, aquí por "onda" nos referimos a una secuencia de ondas, y la longitud de onda se refiere a la distancia entre las crestas de las ondas en la secuencia].

Y esta dependencia se expresa simplemente: momento = h / longitud de onda

h es la famosa constante de Planck , la misma constante fundamental de la naturaleza que la velocidad de la luz. Planck introdujo esta constante en 1900, tratando de desentrañar un misterioso fenómeno físico. Este fue el primer paso hacia la naturaleza cuántica del mundo. Cada vez que intentas describir un fenómeno en el que la mecánica cuántica juega un papel importante, aparece la constante h. En muchas fórmulas puede ver el valor ℏ, y esto es solo h dividido por 2π, ya que este valor suele ser más conveniente para simplificar las fórmulas.


Fig. 1: considere un movimiento cuántico a lo largo de una tira y a lo largo de una tubería

En algunos casos, resulta un poco más fácil explicar qué sucede con el movimiento cuántico a lo largo de la tubería que con lo que se mueve a lo largo de la tira que utilizamos en los ejemplos anteriores. Casi todo lo que funciona para la tubería será cierto para la tira. Por lo tanto, los usaré juntos.

El socio de control de calidad más ligero

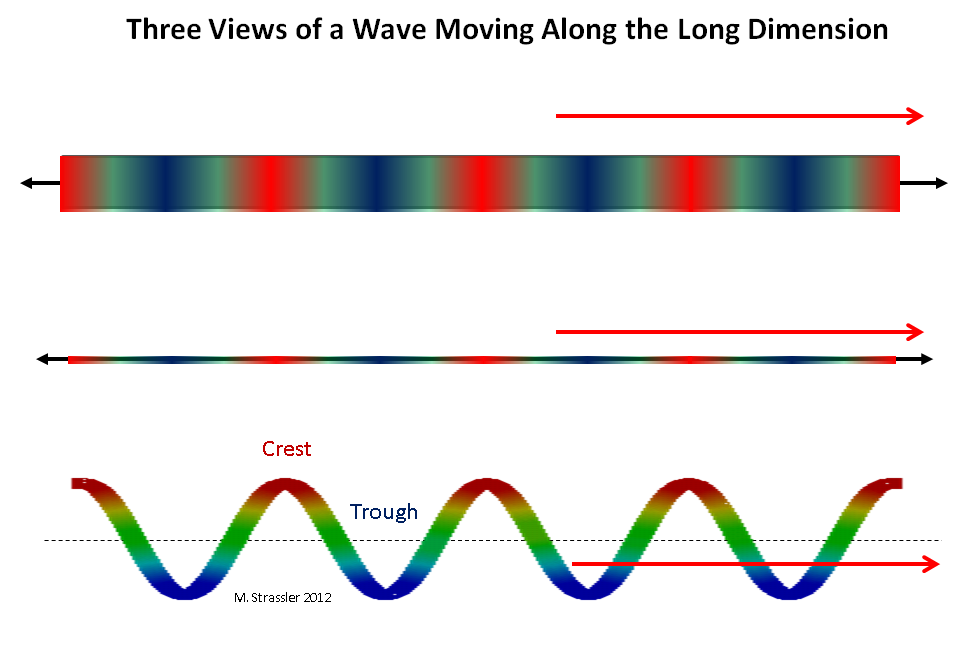Fig. 2: tres vistas de una ola que se mueve a lo largo de una dimensión larga

Imagine un cuántico viajando a lo largo de una franja de ancho W, o a lo largo de un tubo de círculo S. Primero, imagine un cuántico moviéndose a lo largo de una dimensión larga (largo significa infinito, o tanto que puede ser infinito, hasta donde podamos juzgarlo). Una ola que corre a lo largo de una tira o tubería puede moverse a lo largo de una dimensión larga en cualquier dirección y tener cualquier longitud de onda (la distancia entre dos crestas adyacentes). Ver fig. 2. Tal cantidad puede tener cualquier momento a lo largo de una tira o tubería, según De Broglie: el momento puede ser cero, muy pequeño, pequeño, grande, en cualquier dirección, etc. En principio, un impulso se puede hacer un poco más grande (o un poco menos) empujando un cuanto en la dirección de su movimiento (o en el opuesto).


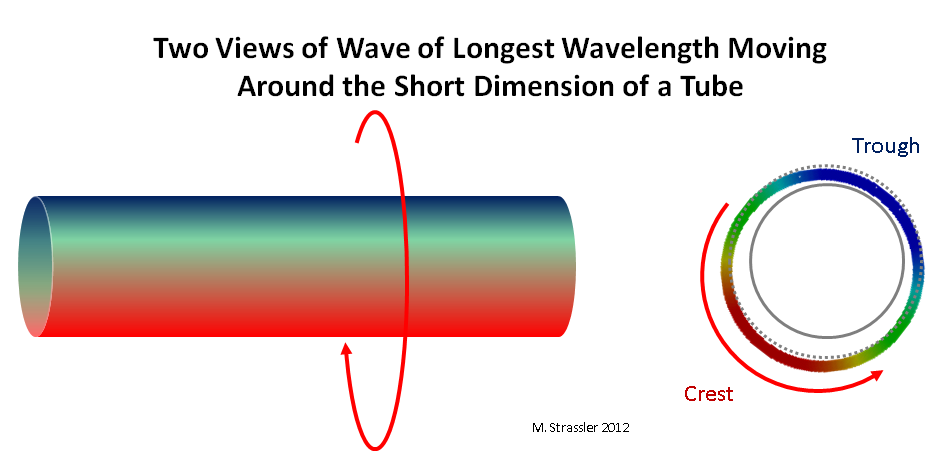Fig. 3: dos vistas de una ola que se mueve a lo largo de una pequeña dimensión de una tubería

Ahora considere un cuanto (es decir, "partícula") que se mueve a través de una tira o tubería. En primer lugar, ¡obviamente no podrá tener una longitud de onda mayor que la distancia transversal de la tira o la circunferencia de la tubería! Esto es fácil de ver en la tubería: al menos una cresta (roja) y una depresión (azul) que se ajustan a lo largo de la tubería, como se muestra en la fig. 3. Si la longitud de onda es mayor que S, la onda no se conectará a sí misma, como se muestra en la Fig. 4. La longitud de onda más larga será exactamente S; y la única cavidad de la ola debe ubicarse exactamente en el lado de la tubería opuesto a la única cresta.


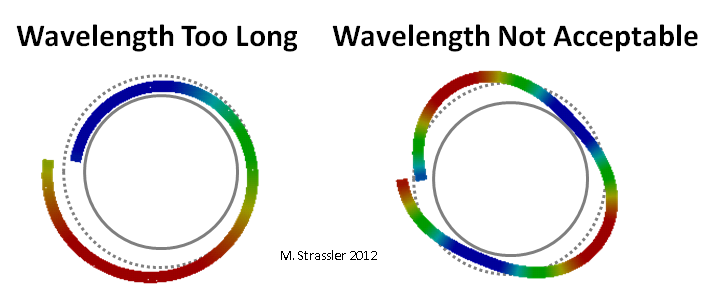Fig. 4: longitudes de onda inadecuadas

La cresta y el valle de la ola en la Fig. 3 se mueven alrededor de la tubería, pareciéndose (Fig. 5) a una partícula ordinaria no cuántica (aquí realmente quiero decir algo como un grano de arena, no una cuántica o una "partícula") rodando a lo largo de la tubería, pero con una diferencia importante: si una partícula intuitiva ordinaria no tiene problemas puede moverse un poco más rápido o más lento, debido a que su impulso aumentará o disminuirá ligeramente, el cuanto correspondiente a la onda no puede tener un impulso ligeramente mayor o menor, ya que esto correspondería a una longitud de onda inaceptable (Fig. 4).


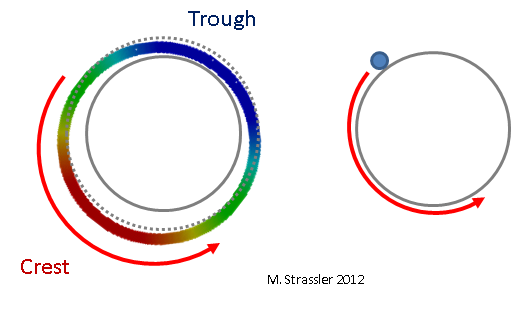Fig. 5: onda similar a una partícula

En una tira es un poco más complicado, pero como se muestra en la fig. 6, de nuevo, solo puede haber una cresta en una pared y una en la otra, y esta situación cambia con el tiempo: la cresta no se mueve, sino que disminuye de tamaño y se convierte en un hueco, y el hueco se convierte en una cresta. Tenga en cuenta que, en contraste con la Fig. 3, donde la cresta y la zanja retienen su tamaño pero se mueven a lo largo de la tubería, la cresta de esta ola no se mueve, sino que se contrae. Por lo tanto, se llama "onda estacionaria". Para un ejemplo similar (pero no idéntico), imagine una cuerda de guitarra o violín. Intuitivamente, esta onda estacionaria corresponde a una partícula ordinaria no cuántica que se mueve hacia adelante y hacia atrás a través de una tira. (Menos intuitivamente, pero más precisamente, corresponde a una partícula ordinaria que se mueve en ambas direcciones al mismo tiempo. Pero este hecho cuántico muy extraño y genial ahora no tiene importancia). Esto se muestra en la Fig. 7)


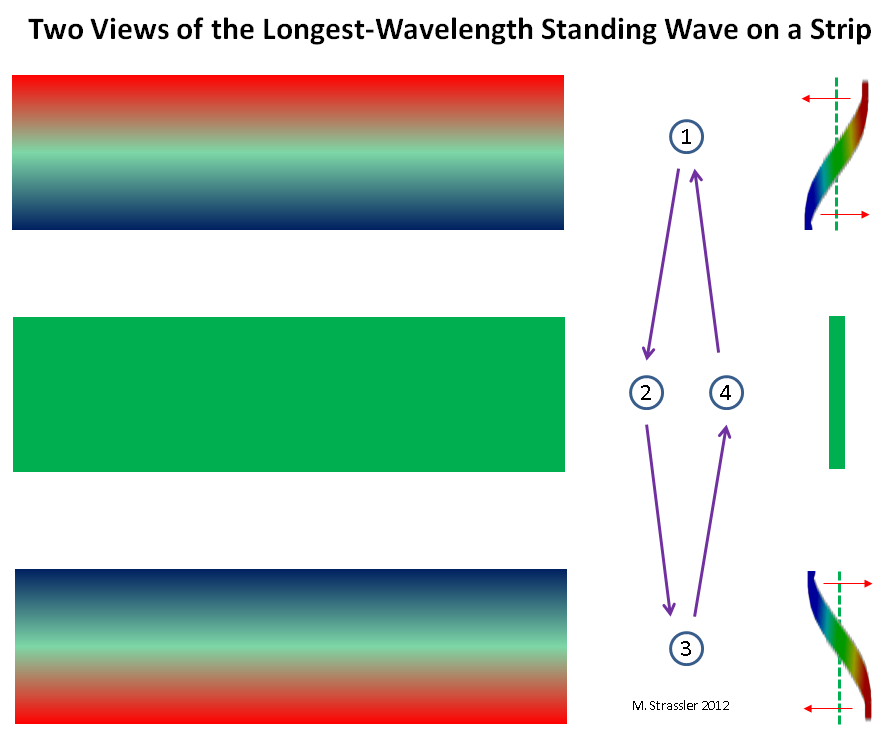Fig. 6: dos vistas de la onda estacionaria con la longitud de onda más larga

En ambos casos, existe la mayor longitud de onda posible (S para tubería, 2W para tira). Y esto significa que existe el menor impulso posible (h / S y h / 2 W para la tubería y la tira). Y finalmente, esto significa que existe la partícula KK más fácil posible. Con masa M, donde

$$

$$M ^ 2 = m ^ 2 + (p_ {través} / c) ^ 2 = m ^ 2 + (h / c S) ^ 2 \ quad (tubería) \\ M ^ 2 = m ^ 2 + (p_ { ancho} / c) ^ 2 = m ^ 2 + (h / 2 c W) ^ 2 \ quad (tira)$$

Tenga en cuenta que para partículas sin masa, m = 0, estas fórmulas se reducen a:

$$

$$M = h / c S \ quad (tubería) \\ M = h / 2 c W \ quad (tira)$$

Y estas últimas fórmulas son aproximadamente correctas si S y W son muy pequeñas, como suele ser el caso en el razonamiento plausible.


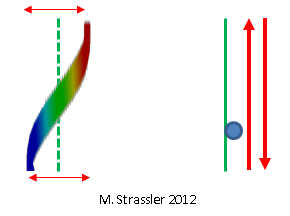Fig. 7: la cantidad de una onda estacionaria es un poco como una partícula que se mueve hacia adelante y hacia atrás

Y así aprendimos que debido al hecho de que las "partículas" son en realidad quanta, con propiedades similares a las propiedades de las ondas:

• En el compañero KK más ligero, la masa M es bastante mayor que m,
• Dado que las fórmulas para M incluyen 1 / W y 1 / S, cuanto menor es la dimensión adicional, más difícil es el compañero KK más ligero.
• De hecho, cuando S y W se vuelven tan pequeños que M excede en gran medida m (o si m es inicialmente cero en absoluto), entonces M es aproximadamente proporcional a 1 / S o 1 / W.

Genial Este es el punto principal, así que asegúrese de comprenderlo antes de continuar. Queda una cosa más por explicar:

• ¿Por qué hay tantos socios KK con diferentes masas M, M ', M ", etc. (donde, por definición, M <M '<M ”, etc.)
• ¿Por qué estas masas están separadas unas de otras?
• ¿Por qué las masas crecen con una dimensión adicional decreciente?
• ¿Por qué los socios KK de diferentes tipos de partículas capaces de moverse en la misma dimensión adicional tienen masas similares, especialmente para los socios KK más pesados?
• Por qué las masas de socios de control de calidad nos darán información directa sobre la forma, el tamaño y la cantidad de mediciones adicionales.

De las respuestas anteriores se puede deducir con bastante facilidad.

Más allá del socio de control de calidad más ligero

Fig. 8: onda más cercana a la longitud de onda más larga, moviéndose a lo largo de la dimensión corta de la tubería

¿Por qué hay muchos socios de KK? Solo porque las ondas cuánticas en una tira o tubo pueden tener muchas longitudes de onda diferentes. En la fig. 8, 9 y 10, se pueden ver ondas con una longitud de 1/2 o 1/3 del máximo, correspondiente (según Einstein y de Broglie) con un cuanto de impulsos dobles y triples con respecto al mínimo.


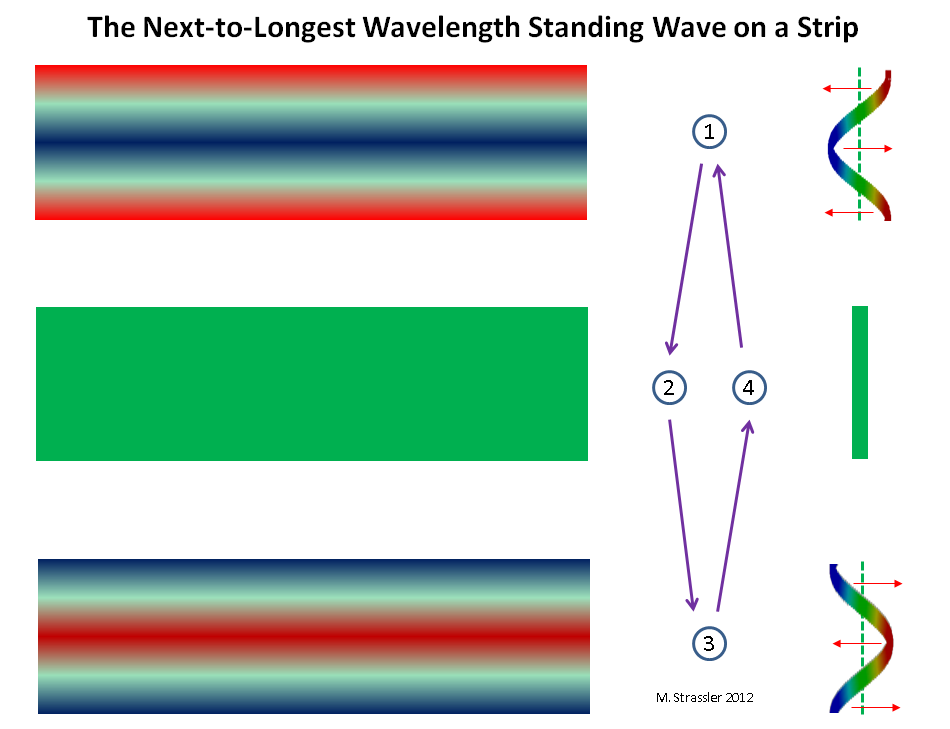Fig. 9 onda estacionaria más cercana a la longitud de onda más larga en la tira

Resumiendo, podemos decir que cualquier longitud de onda es admisible, que tiene n crestas y n canales, donde n es cualquier número entero positivo (1, 2, 3, 4, ..), de modo que la longitud de onda es igual a S dividida por n (o 2W dividido por n) y la onda se ajusta claramente dentro de un círculo de círculo S o dentro de una línea de longitud W. Cualquier otra longitud de onda no es adecuada (ver Fig. 4). En consecuencia, teniendo en cuenta la relación de Broglie, momentum = h / wave_length, se permite cualquier impulso de la forma nh / S (o nh / 2 W), y para cada valor de n tendremos un compañero de masa KK:

$$

$$M ^ 2 = m ^ 2 + (p_ {across} / c) ^ 2 = m ^ 2 + (nh / c S) ^ 2 \ quad (pipe) \\ M ^ 2 = m ^ 2 + (p_ { a través} / c) ^ 2 = m ^ 2 + (nh / 2 c W) ^ 2 \ quad (tira)$$

Esto responde a casi todas las preguntas formuladas, al menos para casos con una tubería y una tira:

• Hay muchos socios de CC (uno para cada n> 0),
• Sus masas están bien separadas entre sí (ya que cuando n cambia por 1, M cambia mucho),
• Sus masas crecen con una disminución en las dimensiones adicionales (ya que los últimos términos en las fórmulas se hacen más grandes cuando W y S se hacen más pequeños),
• Los socios pesados ​​de KK de diferentes partículas con diferentes masas m tienen masas similares M, porque para n lo suficientemente grande los segundos términos en las fórmulas son grandes en comparación con m ² , lo que da la masa del compañero KK aproximadamente igual a M = nh / c S para la tubería y nh / 2 c W para la tira, y es casi independiente de m.

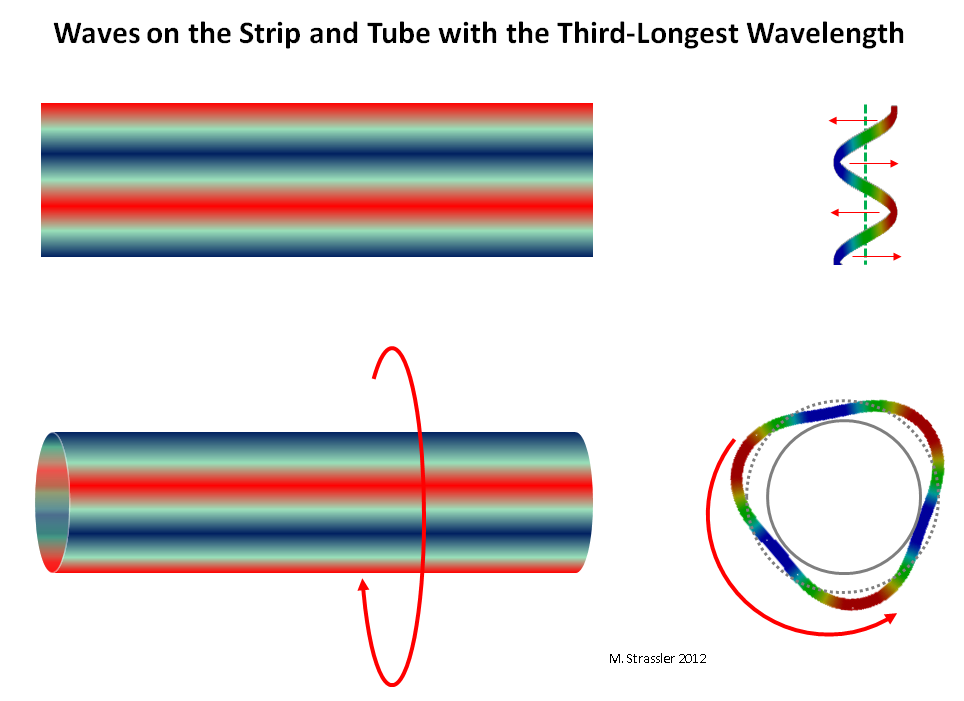Fig. 10: ondas en una tira y una tubería con una longitud de onda de 1/3 como máximo

La última pregunta sigue siendo: ¿por qué la cantidad, el tamaño y la forma de las dimensiones adicionales determinan las masas de los compañeros KK? Y, por lo tanto, por qué la medición de masa de muchos compañeros KK le permite determinar las propiedades de las mediciones adicionales, al igual que escuchar el sonido de un instrumento musical le permite determinar básicamente su forma. , tamaño y materiales de que está hecho?

Tome un ejemplo extremadamente simplificado. Consideraremos dos dimensiones adicionales, nuevamente usando nuestro canal de barco clásico, que incluye (como lo hicimos al final de un artículo reciente con ejemplos de mediciones adicionales) y el hecho de que el canal tiene profundidad, por lo que podemos imaginar las olas dentro de él (ondas de este tipo que puede escuchar en una habitación grande o bajo el agua en cualquier canal). La sección del canal (si la cortamos en cualquier punto de la línea a lo largo de la dimensión larga) será solo un rectángulo de ancho W y profundidad D. Al igual que cualquier partícula no cuántica, incluso si es estacionaria desde el punto de vista de la dimensión larga, puede moverse a lo largo de uno o dos mediciones (y, por lo tanto, tienen un pulso ya sea en ancho o en profundidad), y la onda tendrá una longitud de onda en ambas dimensiones adicionales. Una división tan simple de la onda en lo que hace midiendo el ancho y lo que hace midiendo la profundidad está especialmente vinculada a la rectangularidad del canal, y generalmente no funcionará en otros ejemplos. Por ejemplo, como se muestra en la fig. 11, en la parte superior, una de las ondas permitidas tendrá tres canales para medir el ancho y uno para medir la profundidad.


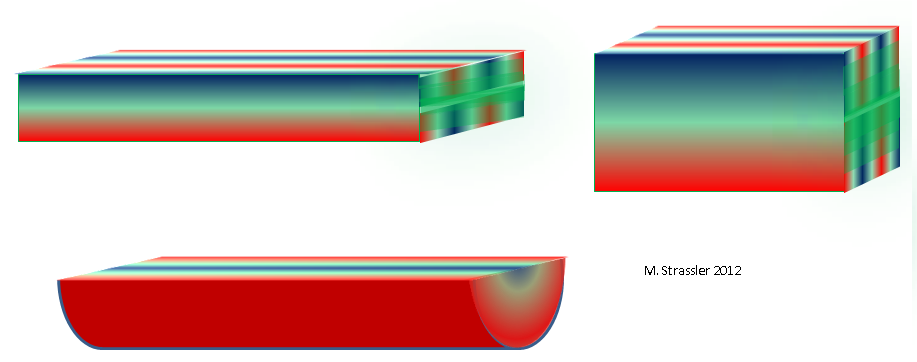Fig. 11

Podemos designar el número de depresiones y crestas midiendo el ancho con el número entero n ₁ , y midiendo la profundidad - n ₂ , y para cada n ₁ y n ₂ (uno o ambos de estos valores pueden ser mayores que cero), obtenemos el compañero KK. Para quanta sin masa (m = 0) o casi sin masa, los socios de KK tendrán masa

$$

$$M ^ 2 = m ^ 2 + (p_ {ancho} / c) ^ 2 + (p_ {profundidad} / c) ^ 2 = m ^ 2 + (n_1 h / 2 c W) ^ 2 + (n_2 h / 2 c D) ^ 2$$

Se puede ver que la distribución de masa es diferente del caso con una dimensión adicional, y que puede decirnos tanto W como D.

Si la sección transversal del canal tiene una forma diferente, por ejemplo, un triangular o medio disco, como se muestra en la Fig. 11, a continuación, obtenemos otra distribución de masa que refleja la forma exacta de un triángulo o medio disco. Y ya podemos descartar los canales prácticos de la nave y representar el espacio tridimensional, cuya sección transversal corresponde a cualquier otra forma bidimensional finita, una de las cuales se muestra en la Fig. 1 en un artículo sobre mundos con dos dimensiones espaciales: un disco completo, o incluso una esfera o toro. Cada una de estas formas nos dará su propio tipo de distribución masiva de socios de control de calidad. Y si habrá tres, cuatro o cinco dimensiones adicionales ... Quizás muchos más tipos de distribuciones.

Los ejemplos de algunas distribuciones para partículas sin masa con tamaños de medidas adicionales elegidos para que las masas de los primeros socios KK sean las mismas para cada caso se dan en la Fig. 12. Es obvio que para establecer la forma y el tamaño de las mediciones adicionales, es necesario medir las masas de un número suficientemente grande de socios KK (e incluso al menos confirmar que cualquiera de las partículas pesadas recientemente descubiertas son generalmente socios KK), por lo tanto, para comprender la naturaleza de cualquier adicional medidas, el tiempo pasará.


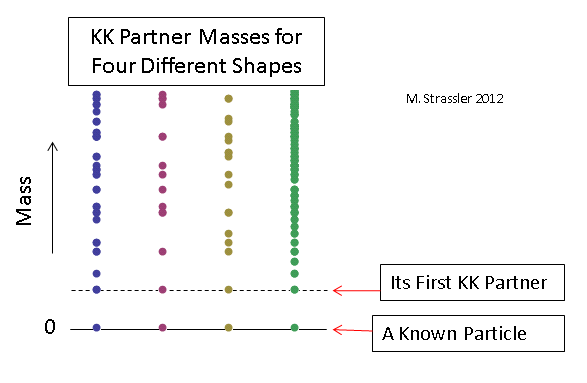Fig. 12

Pero, ¿pueden las partículas pesadas de materia conocidas ser socios KK de las más ligeras?

Entonces surge la obvia pregunta adicional.Sabemos que entre las partículas elementales conocidas hay un electrón, así como sus versiones más pesadas: muón y tau. Hay un quark superior, y sus versiones más pesadas están encantadas y verdaderas. Hay un quark más bajo, y sus versiones más pesadas, extrañas y encantadoras. ¿Son las versiones de partículas pesadas los socios de control de calidad de los pulmones?

A primera vista, esta es una suposición tentadora, pero la respuesta será un firme no. Lo sientoEsta no es una pregunta tonta. Simplemente tiene una respuesta negativa inteligente.

Muon y tau, encantados y verdaderos, extraños y encantadores: todos obtienen sus masas gracias al campo de Higgs, y no gracias al impulso de dimensiones adicionales. Esto se deduce claramente de los experimentos detallados. Se pueden encontrar sugerencias en el artículo sobre lo que sucedería si el campo de Higgs fuera cero . Tenga en cuenta que si el campo de Higgs fuera cero en promedio, entonces el electrón, el muón y la tau no tendrían masa (y cada uno se dividiría en dos tipos de partículas). Esto no corresponde a la teoría de que el muón y la tau son socios KK del electrón.

Hay muchas otras razones. El más grave de ellos, tal vez, será que debido a la presencia de una carga en el electrón y al hecho de que está rodeado por un campo eléctrico, el fotón debe moverse en cualquier dimensión en la que se mueva el electrón (aunque lo contrario no es cierto). Entonces, si el electrón tiene socios KK, entonces el fotón también debería tenerlos. Pero se deduce de nuestras fórmulas (y similares más generalizadas) que dado que el fotón no tiene masa, y la masa de electrones (0.0005 GeV / c ² ) es pequeña en comparación con la masa de muón (aproximadamente 0.1 GeV / c ²), si el muón es un compañero KK, entonces el fotón debe tener un compañero KK de masa similar. Pero tal partícula, si existiera, se habría descubierto hace muchos años. De hecho, los compañeros KK de fotones no se observaron en experimentos en los que se estudiaron masas mucho más grandes que la masa de partículas Z: estos son muchos cientos de GeV / s ² . La partícula Z en sí misma tampoco puede ser un compañero de control de calidad de un fotón; ella no se parece lo suficiente a él. Y esto significa que cualquier compañero KK del electrón debería ser al menos tan pesado.

¿A dónde ir después? A los experimentos

Pasamos de la teoría (la posibilidad de mediciones adicionales, matemáticas y geometría relacionadas) a las predicciones (socios de CC). Siguiente paso: ¿qué sabemos sobre las mediciones adicionales de los experimentos? Todavía no hemos visto socios de KK en los experimentos, pero podemos preguntar, ¿qué podemos aprender de su ausencia? Mucho, como explicaré más adelante, junto con una descripción de cómo los intentos de encontrar signos de mediciones adicionales continúan en el Gran Colisionador de Hadrones y en otros lugares.