Las ecuaciones de Navier-Stokes describen fenómenos cotidianos simples, como el agua que fluye de una manguera de jardín; sin embargo, se basan en un problema cuya solución se estimó en un millón de dólares.

En física, hay ecuaciones que describen todo, desde estirar el espacio-tiempo hasta el vuelo de un fotón. Sin embargo, solo un conjunto de ecuaciones se considera tan matemáticamente complejo que fue elegido como uno de los siete "
Problemas del Milenio ", para el cual el
Instituto de Matemáticas Clay ofrece un premio de un millón de dólares: estas son
las ecuaciones de Navier-Stokes que describen el flujo de fluidos.
Recientemente,
escribí sobre cómo se obtuvo un nuevo resultado importante para estas ecuaciones. Y este trabajo indica que el progreso hacia el Premio del Milenio será más difícil de lo esperado. ¿Por qué estas ecuaciones que describen fenómenos tan familiares como el agua que fluye a través de una manguera son matemáticamente más difíciles de entender que, por ejemplo, las ecuaciones de campo de Einstein, que incluyen objetos tan impresionantes como los agujeros negros?
La respuesta, según tengo entendido, radica en la turbulencia. Todos experimentamos este fenómeno, en vuelo en aire no homogéneo a una altitud de 10,000 m, o al observar un embudo desde el agua que sale del desagüe en el baño. Sin embargo, el conocimiento no se deriva de la conciencia: la turbulencia es una de las áreas menos entendidas del mundo físico.
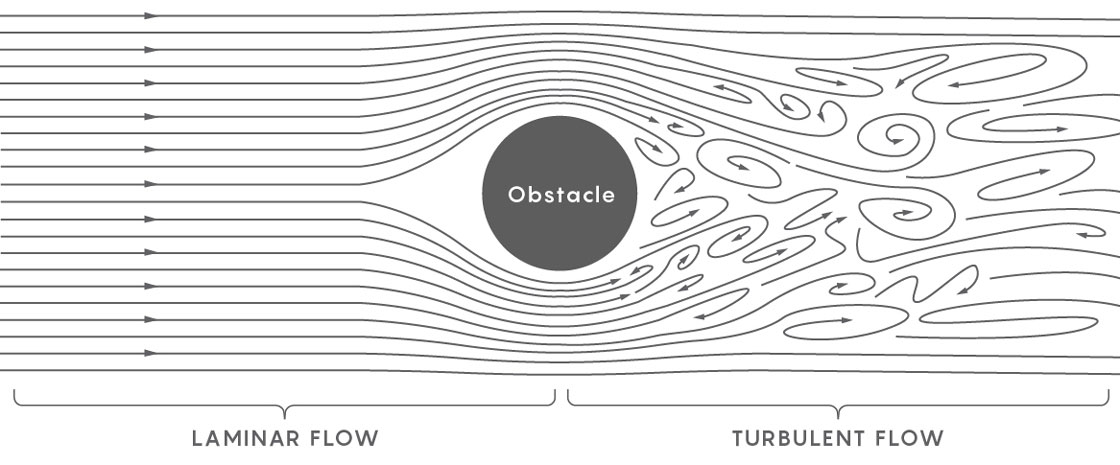
Un ejemplo de flujo sin turbulencia es un río tranquilo. Cada parte se mueve en la misma dirección a la misma velocidad. El fluido turbulento aparece cuando la corriente de un río se rompe, de modo que diferentes partes de la corriente comienzan a moverse en diferentes direcciones a diferentes velocidades. Los físicos describen la formación de turbulencias al principio como la aparición de un embudo en un flujo suave, y luego como la formación de pequeños embudos en el primer embudo, e incluso embudos más pequeños en estos embudos, un mar de embudos que entran en el líquido, de modo que el líquido se rompe en partes discretas, cada una de las cuales interactúa entre sí y se mueve en su propia dirección.
Los investigadores quieren entender exactamente cómo un flujo suave se divide en turbulencias turbulentas y modelar la forma futura del fluido después de que la turbulencia haya pasado factura. Pero el Reto del Milenio está formulado de manera más modesta: solo debe probar que las soluciones siempre existen. Es decir, la pregunta es, ¿pueden las ecuaciones describir cualquier fluido, con alguna condición inicial, y en un futuro infinitamente distante?
"El primer paso es simplemente tratar de demostrar que las ecuaciones tienen algunas soluciones", dice Charlie Fefferman, matemático de la Universidad de Princeton. "Esto no proporciona una comprensión real del comportamiento de los líquidos, pero si tampoco tienes esto, entonces no sabes nada en absoluto".
Entonces, ¿cómo se puede probar la existencia de soluciones? Debe comenzar por comprender por qué podrían no serlo. Las ecuaciones de Navier-Stokes implican el cálculo de cambios en cantidades tales como la velocidad y la presión. Los matemáticos están preocupados por el siguiente escenario: huyes de estas ecuaciones, y después de un tiempo finito te dicen que una partícula fluida se mueve a una velocidad infinita. Y este es el problema: calcular el cambio en el valor infinito no es más fácil que dividir por cero. Los matemáticos llaman a tales situaciones una "explosión", y en el caso de una explosión, las ecuaciones dejan de funcionar y no se encuentran soluciones.
 Las ecuaciones de Navier-Stokes describen el flujo de un fluido incompresible.
Las ecuaciones de Navier-Stokes describen el flujo de un fluido incompresible.
En general, el producto de masa (parte azul) y aceleración (violeta) es igual a las fuerzas que actúan sobre el líquido (naranja):- ρ es la densidad del fluido;
- dV / dt: cambio de velocidad con el tiempo;
- V ∇V - velocidad y dirección de movimiento;
- ∇P - cambio en la presión interna;
- ρ g - la influencia de fuerzas externas (por ejemplo, la gravedad);
- μ ∇ 2 V - la influencia de las fuerzas internas (viscosidad).
La prueba de la ausencia de explosiones (y la existencia de soluciones) es equivalente a la prueba de que la velocidad máxima de cualquier partícula líquida permanece limitada por algún valor finito. Una de las cantidades más importantes es la energía cinética del líquido.
Cuando comienza a simular el flujo utilizando las ecuaciones de Navier-Stokes, su fluido tiene una cantidad inicial de energía. En flujos turbulentos, la energía puede comenzar a concentrarse. En lugar de extenderse uniformemente por todo el río, la energía cinética se puede recoger en remolinos de un tamaño arbitrariamente pequeño, y las partículas en estos remolinos (en teoría) pueden acelerar a una velocidad infinita.
“Con la transición a escalas cada vez más pequeñas, la energía cinética se vuelve cada vez menos útil para el control de decisiones. La decisión puede hacer cualquier cosa, y no sabré cómo controlarla ", dice Vlad Vikol, un matemático de la Universidad de Princeton que escribió un nuevo trabajo con Tristan Buckmaster.
Los matemáticos clasifican ecuaciones parcialmente diferenciales según el grado en que pueden comenzar a comportarse mal en escalas infinitamente pequeñas. Las ecuaciones de Navier-Stokes están en el extremo de esta escala. La complejidad de las matemáticas de las ecuaciones en cierto sentido refleja la complejidad de los flujos turbulentos que deben ser capaces de describir.
"Cuando te acercas a algún lugar, desde un punto de vista matemático, pierdes información sobre la solución", dice Vikol. "Pero la turbulencia debería describir exactamente eso: la transferencia de energía cinética de escalas grandes a escalas cada vez más pequeñas, por lo que realmente te pide que escales".

Hablando de las propiedades matemáticas de las ecuaciones físicas, es natural hacer una pregunta: ¿cambiarán estos argumentos la forma en que consideramos el mundo físico? En el caso de las ecuaciones de Navier-Stokes y el Problema del Milenio, la respuesta será "sí" y "no". Después de casi 200 años de experimentación, está claro que las ecuaciones funcionan: el flujo predicho por Navier-Stokes coincide consecutivamente con el flujo observado en los experimentos. Si usted es un físico que trabaja en un laboratorio, esto puede ser suficiente para usted. Pero los matemáticos necesitan saber más: quieren verificar si es posible seguir estas ecuaciones hasta el final para monitorear exactamente cómo cambia el flujo de un momento a otro (para cualquier configuración de fluido inicial), e incluso para detectar la fuente de turbulencia.
"El comportamiento de los líquidos está lleno de sorpresas", dice Fefferman. "Estas sorpresas se explican, en principio, por las ecuaciones fundamentales que controlan el flujo de fluidos, pero es un misterio cómo pasar de las ecuaciones que controlan el movimiento de un fluido a una descripción de cómo se mueve realmente el fluido".