Dos matemáticos demostraron que, bajo ciertas condiciones extremas, las ecuaciones de Navier-Stokes no tienen sentido
Las ecuaciones de Navier-Stokes con la ayuda de varios términos lacónicos describen uno de los fenómenos más comunes del mundo físico: el flujo de fluidos. Hoy, estas ecuaciones, que datan de la década de 1820, se usan para describir todo, desde las corrientes oceánicas y las turbulencias que siguen a un avión hasta el flujo de sangre al corazón.
Aunque los físicos consideran confiables estas ecuaciones, como un martillo, los matemáticos desconfían de ellas. Para un matemático, el hecho de que estas ecuaciones parecen funcionar no significa mucho. Necesitan pruebas de que las ecuaciones están libres de errores: que para cualquier fluido y para el pronóstico a largo plazo, distribuido en el futuro, las matemáticas de las ecuaciones no fallarán. No fue fácil encontrar esa garantía. La primera persona o equipo que pueda probar que las ecuaciones de Navier-Stokes siempre funcionarán, o proporcionar un ejemplo que demuestre que no funcionan, podrá recibir una recompensa por resolver uno de
los problemas del Milenio , anunciado por
el Instituto Matemático de Clay , y un millón de dólares en Además [a partir de 2017, solo una de las siete tareas del milenio (hipótesis de Poincaré) ha sido resuelta por Gregory Perelman / aprox. transl.].
Los matemáticos han desarrollado muchas formas de resolver este problema. El nuevo trabajo, publicado en septiembre, plantea serias preguntas sobre si uno de los enfoques más populares del problema, desarrollado durante muchos años, puede tener éxito. El trabajo, escrito por Tristan Buckmaster y Vlad Vikol de la Universidad de Princeton, es el primer resultado que muestra cómo, bajo ciertas condiciones, las ecuaciones de Navier-Stokes dan una descripción contradictoria del mundo físico.
"Estamos tratando de comprender ciertos problemas inherentes a estas ecuaciones, y por qué la gente probablemente tendrá que repensarlos", dice Buckmaster.
El trabajo de Buckmaster y Wikol muestra que si hace suposiciones muy aproximadas al resolver las ecuaciones de Navier-Stokes, comienzan a no tener sentido: dicen que el mismo fluido con las mismas condiciones iniciales puede venir en dos o más estados diferentes. Puede fluir de una manera, o de una manera completamente diferente. Si es así, entonces estas ecuaciones no pueden describir de manera confiable el mundo físico para el cual fueron desarrolladas.
Ecuaciones explosivas
Para comprender cómo pueden romperse las ecuaciones, imagine una corriente oceánica. Dentro de su marco, pueden existir flujos locales, como resultado de lo cual algunas de sus partes pueden moverse en una dirección y a una velocidad, y otras en otra dirección a otra velocidad. Los flujos locales interactúan entre sí en la acción mutua constante de la fricción y la presión del agua, que determinan su flujo.
Los matemáticos modelan esta interacción usando un mapa que le informa sobre las direcciones y los caudales en cualquier punto del fluido. Este mapa, llamado campo vectorial, es una instantánea de la dinámica interna de un fluido. Las ecuaciones de Navier-Stokes toman esta imagen y la reproducen como un video, indicando exactamente cómo se verá el campo vectorial en cada momento posterior en el tiempo.
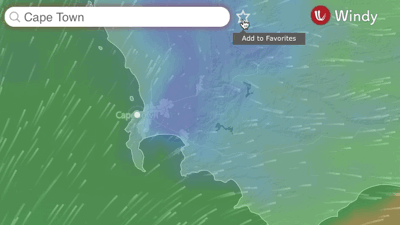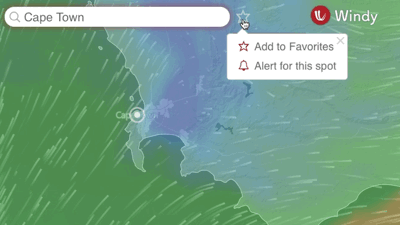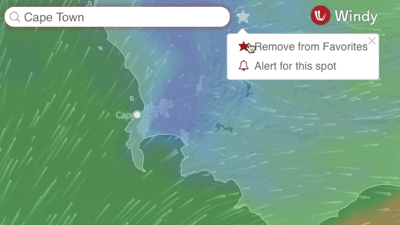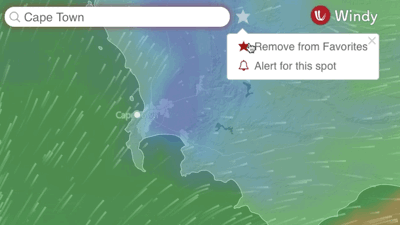El mapa de viento (windy.com) funciona de manera similar a un campo vectorial. En cada punto, el viento tiene una cierta dirección y fuerza.Estas ecuaciones funcionan. Describen el flujo de fluido de manera tan confiable como las ecuaciones de Newton predicen las posiciones futuras de los planetas; los físicos los usan constantemente y coinciden constantemente con los resultados de los experimentos. Sin embargo, los matemáticos necesitan más que una confirmación episódica: necesitan pruebas de que las ecuaciones no se violan, que no importa desde qué campo vectorial comience y hasta qué punto lo reproduzca en el futuro, las ecuaciones siempre le darán Nuevo y único campo vectorial.
Este es el tema del Problema del Milenio, preguntando si las ecuaciones de Navier-Stokes tienen soluciones (la solución, de hecho, es un campo vectorial) para todos los puntos de partida en todos los puntos en el tiempo. Estas soluciones deben garantizar la dirección exacta y la fuerza del flujo en cada punto del fluido. Las soluciones que proporcionan información con una resolución infinitamente pequeña se denominan "fluidas". Para una solución uniforme, cada punto del campo tiene un vector asociado, que le permite viajar "suavemente" alrededor del campo sin atascarse en los puntos donde el vector está ausente, en un punto desde el cual no comprenderá el movimiento adicional.
Las soluciones suaves son una representación completa del mundo físico, pero desde un punto de vista matemático, pueden no existir siempre. Los matemáticos que trabajan en ecuaciones como estas se preocupan por esta situación: ejecuta las ecuaciones de Navier-Stokes y observa los cambios en el campo vectorial. Después de un tiempo finito, las ecuaciones le dicen que cierta partícula de fluido se mueve con velocidad infinita. Entonces tendrás problemas. Las ecuaciones incluyen la medición de cambios en propiedades como la presión, la fricción y la velocidad del fluido, hablando en jerga, toman derivadas de estas cantidades, pero no es más fácil tomar la derivada de una cantidad infinita que dividir por cero. Entonces, si las ecuaciones dan un valor infinito, podemos decir que te rechazaron o "explotaron". Ya no pueden describir los estados posteriores de su líquido.
Tal "explosión" es evidencia de que las ecuaciones carecen de una descripción de algunas propiedades del mundo físico que deben describir. "Quizás las ecuaciones no cubren todos los efectos de un fluido real, porque en un fluido real no esperamos una velocidad de partículas infinita", dice Buckmaster.
La solución al Problema del Milenio es mostrar que las ecuaciones de Navier-Stokes nunca explotan, o encontrar las condiciones bajo las cuales esto sucede. Una de las estrategias utilizadas por los matemáticos es suavizar los requisitos de la precisión con que estas ecuaciones deben describir las soluciones requeridas.
Alteración del flujo
Las ecuaciones de Navier-Stokes deben describir el flujo de cualquier fluido, con cualquier condición inicial, y extender la descripción infinitamente hacia el futuro. Al intentar demostrar esta habilidad, los matemáticos a veces se "debilitan", es decir, usan descripciones aproximadas de campos vectoriales que describen un fluido. Pero hay dificultades con esto.
Idealmente, los matemáticos quieren demostrar que la aplicación de las ecuaciones de Navier-Stokes a cualquier fluido continuo y "liso" producirá un resultado único.
Sin embargo, es más fácil trabajar con campos vectoriales "débiles", no tan detallados. Y los matemáticos han descubierto que algunas descripciones débiles producen resultados no únicos: permiten que el mismo fluido fluya en las mismas condiciones iniciales de dos maneras.
De débil a suave
Cuando los matemáticos estudian ecuaciones como estas, a veces comienzan a ampliar la definición de lo que constituye una solución. Las soluciones fluidas requieren la máxima información: en el caso de Navier-Stokes, requieren que en cada punto del campo vectorial asociado con el líquido exista un vector. Pero, ¿qué sucede si atenuamos los requisitos y decimos que necesita calcular vectores solo para algunos puntos del campo, o necesita obtener solo valores aproximados de los vectores? Tales decisiones se llaman "débiles". Permiten a los matemáticos sentir el comportamiento de la ecuación sin el tedioso trabajo de encontrar absolutamente todas las soluciones (lo que en la práctica puede no ser posible).
Tristan Buckmaster, matemático de la Universidad de Princeton"Desde algún punto de vista, las decisiones débiles son aún más fáciles de describir que las reales, porque necesitas saber mucho menos", dijo Camillo De Lellis, coautor de Lazlo Schekelikhidi, quien escribió varios trabajos importantes que sentaron las bases para el trabajo de Buckmaster y Vikola.
Las soluciones débiles vienen en diferentes grados. Si imagina una solución suave en forma de una imagen matemática de un líquido con resolución infinita, entonces las soluciones débiles serán algo así como versiones de 32 bits, 16 bits u 8 bits de esta imagen.
En 1934, el matemático francés
Jean Leray definió una clase importante de soluciones débiles. En lugar de trabajar con vectores exactos, las "soluciones de Leray" toman el valor promedio de los vectores en un pequeño vecindario del campo vectorial. Leray demostró que siempre puede resolver las ecuaciones de Navier-Stokes, permitiendo que sus decisiones tomen la forma de este tipo. En otras palabras, las decisiones de Lera no explotan.
El logro de Lera determinó un nuevo enfoque para el problema de Navier-Stokes: comience con las soluciones de Lera, cuya existencia ya se conoce, y vea si pueden convertirse en soluciones fluidas cuya existencia quiera probar. Este proceso se asemeja a aquel en el que comienzas con una imagen aproximada y ves si puedes cambiar gradualmente la resolución para lograr la imagen perfecta de la realidad.
"Una de las estrategias posibles es mostrar que estas decisiones débiles de Lera son suaves, y si puedes demostrar que son suaves, resolverás el Desafío del Milenio", dijo Bakmaster.
Vlad Vkol representa a la mitad del equipo que reveló problemas en el enfoque para verificar las ecuaciones de Navier-Stokes.Hay otra trampa. Las soluciones de las ecuaciones de Navier-Stokes corresponden a eventos físicos reales, y los eventos físicos ocurren de una manera posible. Dado esto, me gustaría que sus ecuaciones tengan solo un conjunto de soluciones únicas. Si las ecuaciones le dan muchas soluciones posibles, no pueden hacer su trabajo.
Por lo tanto, los matemáticos podrán usar las soluciones de Leray para resolver los problemas del Milenio, solo si las soluciones de Leray son únicas. Las soluciones de Leray no únicas significarán que, de acuerdo con las reglas de Navier-Stokes, el mismo fluido con las mismas condiciones iniciales puede llegar a dos estados físicos diferentes, lo que no tiene un significado físico e implica que las ecuaciones en realidad no describen que deberia
El nuevo resultado de Bakmaster y Wikol es la primera pista de que, para ciertas definiciones de decisiones débiles, esto puede suceder.
Muchos mundos
En su nuevo trabajo, Buckmaster y Wikol consideran soluciones aún más débiles que las soluciones de Leray, soluciones que utilizan el mismo principio de promedio que el de Leray, pero debilitan un requisito adicional más (conocido como la desigualdad energética). Utilizan el método de "integración convexa", que se origina en el trabajo sobre la geometría del matemático John Nash, y luego participa en el estudio de los líquidos por De Lellis y Schekelikhidi.
Con este enfoque, Buckmaster y Wikol demuestran que estas soluciones muy débiles de las ecuaciones de Navier-Stokes no son únicas. Por ejemplo, demuestran que si comienza con un líquido completamente tranquilo, por ejemplo, con un vaso de agua al lado de la cama, son posibles dos tipos de eventos. Lo primero es obvio: el agua comienza con un estado de calma y siempre permanece en calma. El segundo es fantástico, pero matemáticamente posible: el agua comienza desde un estado tranquilo, explota en medio de la noche y luego regresa a un estado tranquilo.
"Esto demuestra la falta de unicidad, porque al menos dos objetos pueden construirse a partir de los datos iniciales", dice Vikol.
Buckmaster y Wikol demostraron la existencia de muchas soluciones débiles no únicas (no solo las dos descritas anteriormente) de las ecuaciones de Navier-Stokes. La importancia de esta evidencia queda por entender. En algún momento, las soluciones débiles pueden volverse tan débiles que dejan de estar relacionadas con soluciones más suaves que deberían imitar. Si esto es así, entonces el resultado obtenido por Bakmaster y Wikol conducirá a poco.
“Este resultado es claramente una advertencia, pero se puede argumentar que esta advertencia se refiere a la idea más débil de decisiones débiles. Hay muchas capas de soluciones más fuertes que puede esperar para un comportamiento mucho mejor "en el caso de las ecuaciones de Navier-Stokes", dice De Lellis.
Backmaster y Wikol también piensan en términos de capas, y fijó su mirada en las decisiones de Lehr, al demostrar que también admiten múltiples físicas en las que el mismo fluido del mismo estado puede adoptar diferentes formas en el futuro.
"Tristan y yo creemos que las decisiones de Leray no son únicas. Todavía no hemos demostrado esto, pero nuestro trabajo establece la cabeza de puente para un ataque en esta tarea ”, dijo Vikol.