Paso de Venus en el disco del Sol y determinación de la distancia entre ellos.

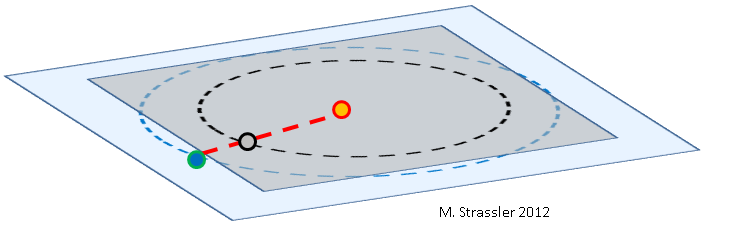
Fig. 1: Tierra (azul), Venus (gris) y el Sol (naranja), no a escala.

Con respecto al paso de Venus a través del disco del Sol en 2012, ya se han escrito muchos artículos . Acerca de cuán raramente ocurre este evento y por qué exactamente: en teoría, Venus, moviéndose alrededor del Sol con más frecuencia que la Tierra, debería pasar entre la Tierra y el Sol durante cada uno de sus giros (Fig. 1), pero porque las órbitas de dos planetas no están alineadas (no están en el mismo plano, ver Fig. 2), Venus a menudo pasa por encima o por debajo del Sol desde el punto de vista de la Tierra.

Pero en lugar de repetir las palabras de otros, quiero agregar algunos detalles que no son tan fáciles de encontrar en Internet.

Es posible que haya leído que con la técnica basada en el razonamiento del astrónomo Edmund Halley (el famoso cometa Halley) hecho por él desde 1678 a 1716, así como a James Gregory antes que él, el paso de Venus en 1716 se utilizó para determinar la distancia de la Tierra a El Sol (y antes de Venus, y todos los demás planetas) con un error del 2% es el más alto de los alcanzados en ese momento. Se esperaba que la precisión fuera 10 veces mayor, pero un efecto óptico inesperado llamado " efecto de gota negra " intervino en el proceso; todavía hay debates sobre las razones exactas de su aparición. Pero es posible que no haya leído que esta medición, y muchas otras mediciones de distancias en astronomía, hasta estrellas espaciadas bastante cercanas, se basa en el principio de paralaje , en el mismo hecho geométrico que utilizan nuestros ojos y cerebro para percibir la profundidad, o nuestra capacidad de sentir qué tan lejos están los objetos de nosotros simplemente mirándolos.


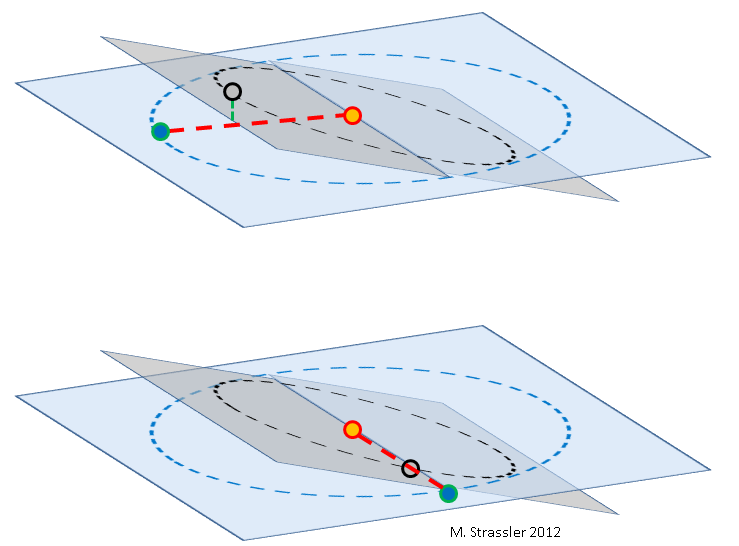Fig. 2: Tierra (azul), Venus (gris) y Sol (naranja), no a escala. La órbita de Venus (un círculo negro en un rectángulo gris) está inclinada con respecto a la órbita de la Tierra (un círculo azul en un rectángulo azul). El grado de inclinación es muy exagerado. Dado que la Tierra y Venus giran alrededor del Sol a diferentes velocidades, pueden cruzarse en cualquier punto de las órbitas.

Arriba: durante este pasaje, Venus se encuentra arriba o debajo (línea verde) de la línea que conecta la Tierra y el Sol (línea roja), por lo que Venus no pasa a través del disco solar.

Abajo: en casos raros, la línea que conecta la Tierra y el Sol coincide con la línea de intersección de los planos de las órbitas, y Venus está cerca de la misma línea, que conduce al pasaje.

Sin paralaje, también es fácil determinar la distancia relativa de Venus al Sol, es decir, la relación del radio de la órbita de Venus L _V al radio de la órbita de la Tierra L _E. Por lo tanto, en astronomía del Renacimiento, las distancias relativas de los planetas a la Tierra y al Sol se calcularon bastante temprano. Pero para determinar L _V y L _{E por} separado, es necesario medir el paralaje, y el paso de Venus puede proporcionarlo. El paso de Venus en la década de 1760 dio una medida bastante precisa de L _E - L _V , la distancia "absoluta" de la Tierra a Venus; Esto hizo posible averiguar L _E , L _V y las distancias a todos los demás planetas con un error de un par por ciento. Antes de esto, a fines del siglo XVII, se realizó una medición de la distancia de la Tierra a Marte, que tuvo un error de aproximadamente el 10%; También se basó en paralaje, pero esta es una historia completamente diferente.

Comentario preliminar: la Tierra y Venus, e incluso el Sol son muy pequeños en comparación con las distancias entre ellos, por lo que es casi imposible dibujar imágenes precisas. En las ilustraciones, siempre debes dibujar planetas más grandes de lo que realmente son, en relación con las distancias entre ellos, solo para que puedas entender el concepto. ¡Ten esto en cuenta! Todas mis ilustraciones no están dibujadas a escala.

Los tamaños relativos de las órbitas de Venus y la Tierra.

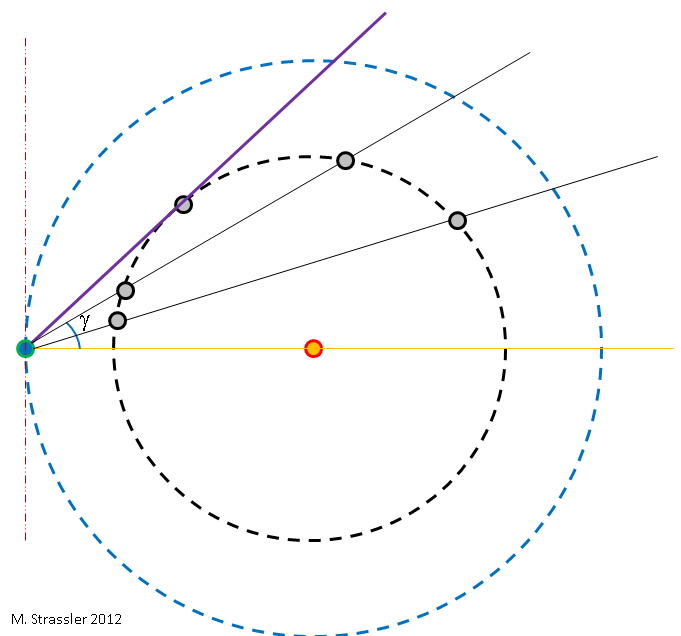Fig. 3

Para comprender la razón principal de la simplicidad de la determinación de L _V / L _E , suponga que las órbitas de la Tierra y Venus son circulares y alineadas: se encuentran en el mismo plano (como se muestra en la Fig. 1, isométrica, y en la Fig. 3 es una "vista superior"). De hecho, las órbitas de la Tierra y Venus están ligeramente alargadas y no están alineadas (Fig. 2). Pero la elipticidad y la falta de coincidencia de los planos no son muy importantes para nuestro razonamiento, por lo que primero podemos ignorarlos y luego recordar nuevamente para obtener respuestas más precisas.

Aquí aplicaremos la tecnología clásica para la física: haremos una aproximación suficiente para la tarea actual y no profundizaremos más de lo necesario. Esta es una forma muy poderosa de pensar sobre la ciencia y el conocimiento en general: es suficiente para responder cualquier pregunta con un cierto nivel de precisión, por lo que puede usar la técnica más simple de las que le proporcionarán el nivel deseado de precisión. Este método se ha utilizado perfectamente durante siglos y es aplicable no solo a la física.

Por lo tanto, tomaremos la aproximación en la cual las órbitas son circulares y alineadas, y recibiremos aproximadamente las respuestas correctas, con un error de un pequeño porcentaje. Esto será suficiente para demostrar los conceptos básicos que busco. Créeme, puedes hacer cálculos mucho más precisos, o puedes convertirte en un experto en este asunto tú mismo. Pero nuestra aproximación no solo dará una muy buena respuesta, sino que también podrá mostrar por qué es tan fácil calcular la relación de L _V a L _E , pero no los valores de L _V y L _E.

Durante el año en que la Tierra y Venus giran alrededor del Sol a diferentes velocidades, la posición relativa de la Tierra y Venus con respecto al Sol cambia. Si en un día determinado (día, mes, año) decido hacer un dibujo con el Sol en el centro y con la Tierra a la izquierda, como en la Fig. 2, entonces Venus puede estar en cualquier lugar de su órbita. Esto significa que desde el punto de vista de la Tierra, el ángulo entre Venus y el Sol en el cielo cambiará dependiendo de la fecha. Esto se muestra en la fig. 3, donde el ángulo se llama γ. El ángulo es fácil de medir; encuentre a Venus en el cielo después del atardecer o antes del amanecer y mida el ángulo entre Venus y el Sol; ver foto 4)


Fig. 4 4

De la fig. La Figura 3 muestra que γ tiene un tamaño máximo: el ángulo entre las líneas naranja y púrpura. Moviéndose en órbita, Venus aparecerá en otro lugar con cada puesta de sol; durante algún tiempo se elevará por encima del horizonte durante varias noches seguidas, y luego gradualmente comenzará a aparecer debajo. Observando a Venus durante varias noches seguidas y midiendo γ, podemos determinar el valor máximo de γ, que llamaré γ _max .

De la fig. 3 es obvio que (como se muestra en la Fig. 4) γ _{max es} inferior a 90 °, ya que la línea violeta debe estar entre la naranja y la roja, perpendicular. Geométricamente, esto es una consecuencia del hecho de que Venus siempre está más cerca del Sol que la Tierra. Estos ángulos explican por qué Venus siempre es visible, ya sea inmediatamente después del atardecer o antes del amanecer (excepto los días en que se encuentra detrás del Sol). Venus no puede estar en su cenit después del anochecer, porque para esto tendría que estar a la izquierda de la línea roja.


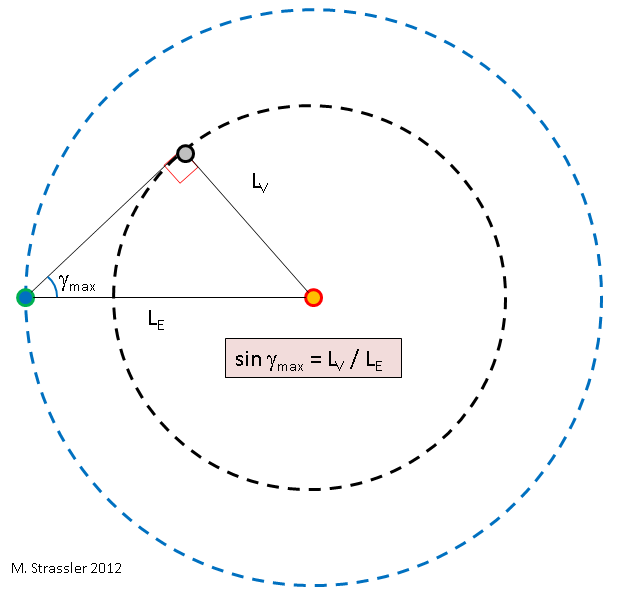Fig. 5 5

Ahora podemos determinar la relación de los radios de dos órbitas - L _V a L _E - usando γ _max . Esta es la geometría más simple, ver fig. 5. La conclusión es que cuando Venus está en el ángulo máximo del Sol, la línea entre el Sol y Venus es perpendicular a la línea entre la Tierra y Venus, por lo que las líneas que conectan estos tres objetos forman un triángulo rectángulo. A partir de aquí, obtenemos trigonometría estándar:

$$

$$L_V / L_E = \ gamma_ {max}$$

Y a partir de aquí, con la ayuda de otras fórmulas geométricas simples, obtenemos la relación entre las distancias a otros planetas.

Esto no es del todo exacto, por las razones indicadas al principio; Las órbitas de los planetas son elipses, y no se encuentran en el plano del agua. En otras palabras, L _V y L _E no se almacenan durante el año, y γ _max se aplica un poco más complicado, en tres dimensiones, como en la Fig. 2, pero no en dos, como en la Fig. 1, 3 y 5. Pero con la ayuda de mediciones precisas de la posición de Venus y el Sol en el cielo, es posible determinar las órbitas exactas de Venus y la Tierra alrededor del Sol y mejorar los cálculos. El significado es el mismo; Todas las mediciones de la posición de Venus y el Sol en el cielo solo nos permiten medir los tamaños relativos de las órbitas de Venus y la Tierra. Pero los valores exactos de L _V y L _E no se pueden determinar de esta manera. Aquí necesitamos un enfoque diferente.

Paso de Venus, paralaje y distancia al Sol.

La razón por la cual el paso de Venus le permite medir los valores absolutos de las órbitas de la Tierra y Venus es que este proceso se puede observar con alta precisión desde diferentes lugares del globo, como resultado de lo cual tendrá dos perspectivas de la ubicación visible de Venus en relación con el Sol, medido desde diferentes lugares con conocidos distancia entre ellos La medición de paralaje le permite determinar el valor absoluto de la distancia de la Tierra a Venus desde el ángulo de paralaje y la distancia entre dos puntos de medición en la Tierra, al igual que un tipo diferente de objeto para los ojos izquierdo y derecho permite que nuestro cerebro nos dé una sensación de profundidad, una sensación de distancia de los objetos.


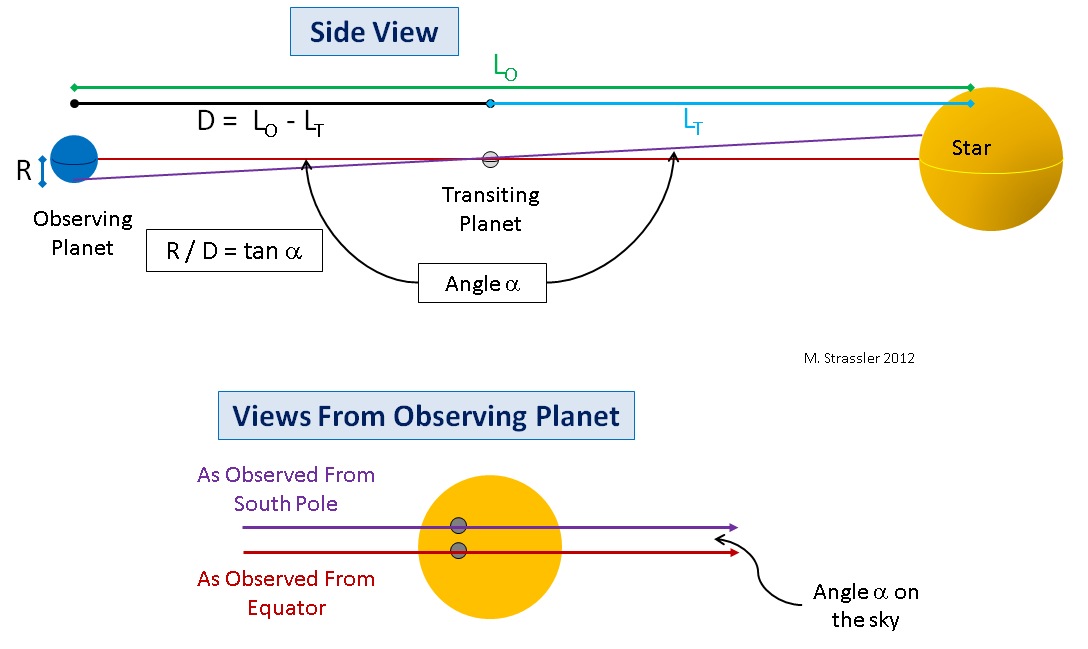Fig. 6 6

Para una demostración, permítanme dibujar cómo se verá desde un gran planeta. En la fig. La figura 6 muestra el planeta con el que observaremos el pasaje (será la Tierra) y el planeta que pasa frente a la estrella (será Venus). Presentaré una situación simplificada (solo para hacer la geometría más simple y el concepto principal más fácil de ver), en el que los planetas y la estrella están alineados, por lo que desde el punto de vista del observador en el ecuador, un planeta que pasa pasará a lo largo del ecuador de la estrella. Arriba en la fig. 6 muestra una vista lateral; observe la línea roja desde el ecuador del planeta observador hasta la estrella a través del ecuador del planeta que pasa a través del disco de la estrella.

En el caso de una alineación perfecta, el observador en el ecuador del planeta externo verá cómo el planeta interno pasa a lo largo del ecuador de la estrella. Esto se muestra como una línea roja en la parte inferior de la fig. 6. Pero el observador del polo sur del planeta exterior verá cómo el planeta interior pasa la estrella a lo largo del camino (línea púrpura) al norte del ecuador de la estrella (en el caso del polo norte, todo será al revés). Si medimos el ángulo α en el cielo entre los caminos a lo largo de los cuales se mueve un planeta que pasa y conocemos el radio R del planeta observador, ¿podemos dibujar un triángulo rectángulo que conecte el planeta que pasa, el centro del planeta observador y el polo del planeta observador, con un ángulo pequeño? La trigonometría simple nos dará la distancia D entre los planetas durante el paso, donde

$$

$$D = R / tan \; \ alpha$$

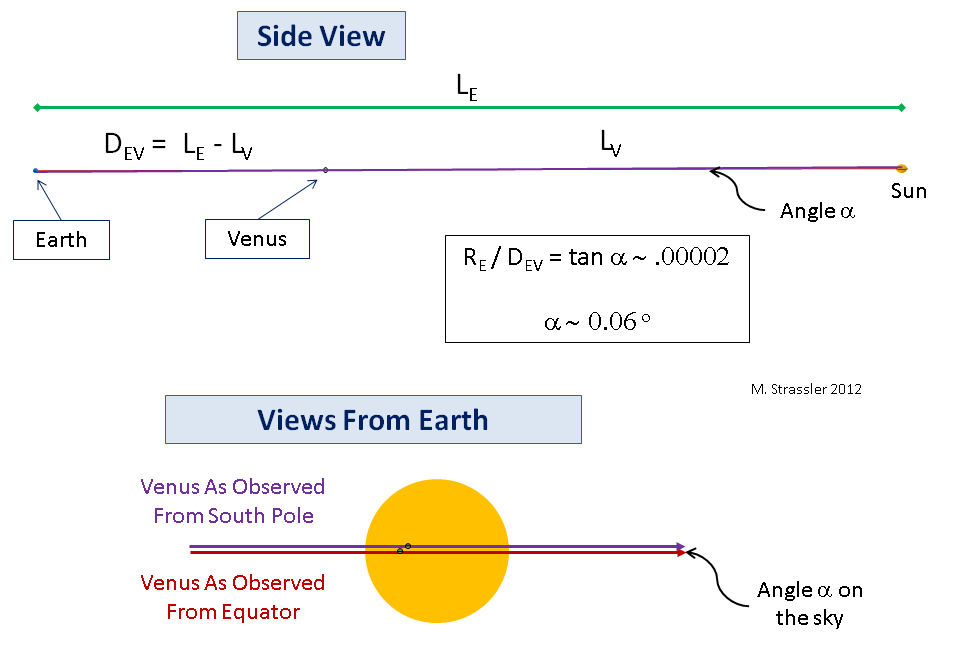Fig. 7 7

Lo mismo es cierto para la Tierra, Venus y el Sol, ¡excepto que la Tierra y Venus son tan pequeños en comparación con la distancia entre ellos y el Sol que el ángulo α será igual a aproximadamente 1/20 °! (Esta es una cantidad bastante pequeña, pero bastante medible, aunque una medición exacta de la distancia al Sol, que los astrónomos del siglo XVIII querían obtener, requeriría una medición técnicamente precisa bastante complicada de la magnitud de un ángulo pequeño). No dibujaré un ángulo tan pequeño, así que debes creer que lo que está sucediendo es una versión de lo que he representado en la fig. 6, con planetas y una estrella (el Sol) mucho más pequeña que la pintada allí, con respecto a las distancias. Incluso la imagen en la fig. 7 hace que los planetas sean mucho más grandes de lo que son. Pero la idea permanece sin cambios: la distancia D _EV entre la Tierra y Venus durante el paso se puede determinar midiendo el ángulo de paralaje α (parte inferior de la Fig. 7; tenga en cuenta que el diámetro angular del Sol es aproximadamente 1/2 °).

Sin embargo, todavía hay muchas preguntas:

• Le dije cómo medir D _EV , la distancia de la Tierra a Venus durante el pasaje. ¿Pero no era nuestro objetivo medir L _E y L _V , la distancia de la Tierra al Sol y de Venus al Sol?
• Nadie fue al polo sur de la Tierra para observar el paso de Venus en 1761 o 1769.
• Asumí órbitas perfectamente alineadas de la Tierra, Venus y la posición del Sol, de modo que desde un punto en el ecuador de la Tierra se podía ver a Venus moviéndose a lo largo del ecuador del Sol. Pero en realidad este no es el caso, e incluso no parece un tutorial típico (y en 2012 tampoco lo fue).
• El ángulo α es lo suficientemente pequeño como para ser medido con precisión, especialmente en los días previos a la fotografía y la mensajería instantánea, en ausencia de indicaciones claras de la ubicación del polo norte del Sol, lo que dificulta la comparación precisa de las mediciones del camino de Venus hechas desde dos puntos diferentes en la Tierra. Sin embargo, el objetivo principal era medir el ángulo no peor que 1 parte de 500 (0.2%) (aunque debido al efecto de caída negra, el resultado fue más cercano a 1 parte de 50 (2%)).

¿Cómo hacer frente a estos problemas?

Primero, ¿cómo pasa de medir D _EV a medir los valores deseados, L _E y L _V ? Es simple: ya conocemos todas las relaciones, en particular, ya sabemos L _E / L _V (aproximadamente, de la Fig. 4, o, si abordamos el problema con más cuidado, podemos calcular y con mayor precisión) desde el ángulo máximo γ _max entre Venus y El sol desde el punto de vista de la Tierra. También sabemos D _EV = L _E - L _V = L _E (1 - L _V / L _E ) de la Fig. 7. Por lo tanto, podemos obtener un valor aproximado de L _E usando:

$$

$$L_E = D_ {EV} / (1 - L_V / L_E) = R / tan \; α / (1 - sin \; \ gamma_ {max})$$

donde α es el ángulo de paralaje medido durante el tránsito, y γ _max es el ángulo máximo entre Venus y el Sol (Fig. 5). Las mediciones más precisas requieren una geometría más compleja, pero con la misma idea básica.

En segundo lugar, incluso si las órbitas de los planetas estuvieran perfectamente alineadas, no es necesario medir dos dimensiones del camino de Venus desde el ecuador y el polo de la Tierra. Se pueden medir desde dos latitudes cualquiera. La geometría se vuelve un poco más complicada, pero no mucho, pero el principio permanece (ver Fig. 8).


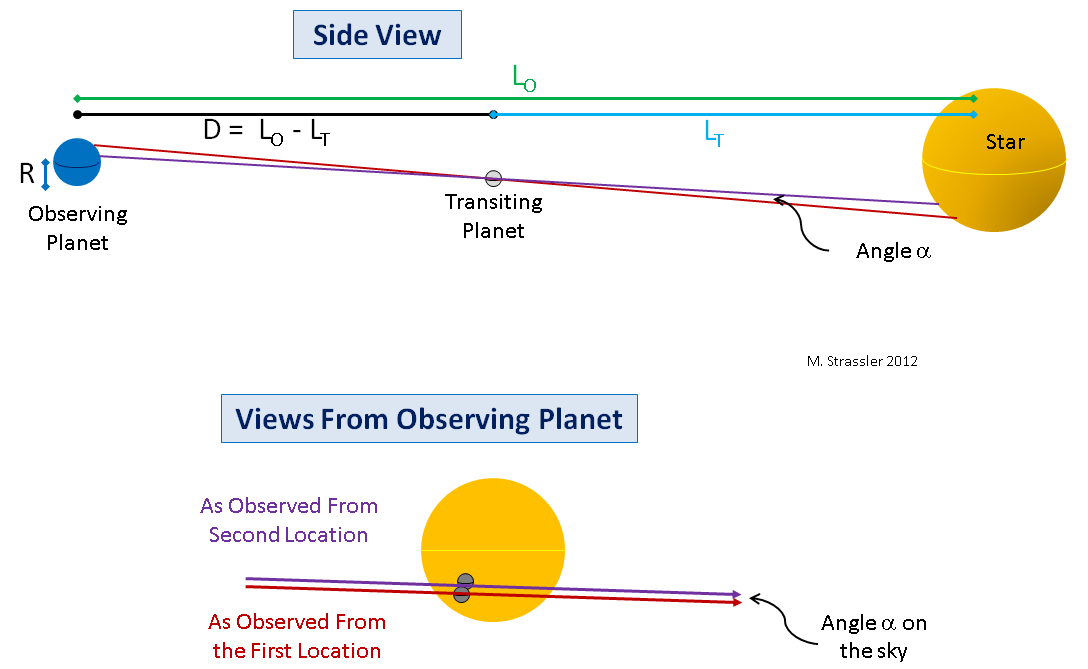Fig. 8

Tercero, incluso sin una alineación perfecta, aparecerá un pequeño ángulo de paralaje al medir valores desde dos puntos diferentes de la Tierra, y si este ángulo se mide bien, esta medición se puede convertir (a través de ecuaciones un poco más complejas) en D. Esto se muestra en la Fig. 8, abajo.

La cuarta pregunta es el problema históricamente complejo de medir el desplazamiento angular del camino de Venus mientras pasa a través del ángulo α nos lleva a un intento alternativo de medir el tiempo, ya sea el tiempo de viaje, o simplemente el principio y el final del pasaje, y no los ángulos. La primera opción fue propuesta por Halley basada en las ideas de Gregory, y la segunda, como una mejora adicional, fue propuesta por Joseph Nicola Delille . El método Halley no requería sincronización de reloj en diferentes lugares de la Tierra; El método requerido de Delil, por lo tanto, se basaba en una tecnología de reloj más avanzada.

Incluso en el siglo XVII o XVIII es mucho más fácil medir con precisión el intervalo, o los momentos del comienzo y el final del eclipse, que medir con precisión la ubicación de Venus en relación con el disco del Sol, especialmente en ausencia de fotografía. En la fig. La Figura 9 muestra que los caminos violeta y rojo de Venus que cruza el Sol tienen longitudes ligeramente diferentes porque no lo cruzan en un lugar, lo que significa que la duración del pasaje será diferente según el tiempo asociado con el ángulo de paralaje. Desafortunadamente, todo resulta ser más complicado de lo que parece a primera vista: la Tierra gira y se mueve alrededor del Sol, por lo que el observador recorre una distancia bastante considerable durante el paso de Venus a través del disco del Sol. Por lo tanto, se requiere mucho esfuerzo (los cálculos son bastante complicados, aunque con las computadoras modernas son mucho más simples) para determinar la diferencia en los intervalos de tiempo del comienzo y el final del pasaje observado por dos observadores diferentes en la Tierra, dependiendo de la distancia al Sol.

Halley a principios del siglo XVIII entendió todos los principios geométricos necesarios (si resta la fraseología y el estilo inglés obsoleto de sus textos, se sorprenderá de cómo sus declaraciones complejas suenan modernas, y verá que los científicos hace trescientos años eran muy similares a los científicos de hoy en día, poseía la misma inteligencia y solo le faltaba la tecnología científica de hoy).


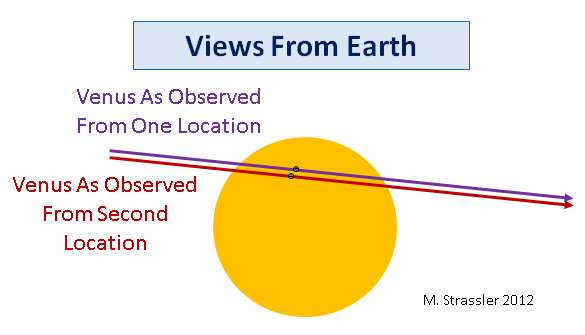Fig. 9 9

Todo esto sugiere que el paralaje, la diferencia en la posición visible atribuida a Venus con respecto al Sol desde el punto de vista de los observadores que lo miden al mismo tiempo pero desde diferentes lugares de la Tierra, ha sido históricamente un método muy importante por el cual determinó el tamaño del sistema solar. Hoy, tenemos a nuestra disposición métodos más potentes, pero puede interesarle el hecho de que lo que ve hoy en el cielo es de gran importancia histórica, o simplemente puede disfrutar de la vista de Venus, moviéndose majestuosamente alrededor de nuestra estrella.