
Entonces eres un programador. ¿Por qué necesitas polinomios? Por ejemplo, entonces, que es una buena arcilla geométrica, desde la cual puedes moldear diferentes cosas.
De nuestro
artículo que explica la esencia del análisis matemático usando Python, sangre y dinamita como ejemplo, se puede ver que puede analizar y sintetizar funciones arbitrarias como polinomios. Sin embargo, no es necesario trabajar específicamente con funciones. A veces es posible que necesite modelar una spline desde varios puntos o propiedades, como tangentes de curvas. Por ejemplo, necesita hacer algún tipo de animación, o un buen efecto de video, o dibujar una curva que pase por ciertos puntos, o crear una superficie que sea plana en un lugar y curvada en otro.
Los polinomios, incluso los spline, pueden no ser siempre la mejor herramienta para esta tarea, pero poseen algunas características que los programadores realmente aprecian. Son simples y versátiles por naturaleza y, lo más importante, muy efectivos en términos de rendimiento. Tomemos por ejemplo el siguiente polinomio:
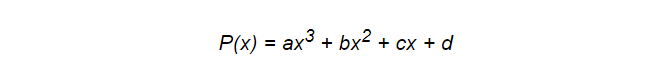
Para calcularlo, solo se requieren 6 acciones de multiplicación y 3 adiciones. Esto es importante porque su modelo estará constantemente sujeto a cálculos. Pero aquí podemos realizar la optimización. El esquema de Horner nos ayudará con esto. Con su ayuda, se puede escribir el mismo polinomio que

Y esto es solo 3 multiplicaciones y 3 adiciones. Verá, acabamos de comenzar y ya aprendió a deshacerse de un tercio de los cálculos.
Interpolación polinómica
La tarea de adaptar un polinomio de grado
n a
n + 1 puntos en el espacio se llama interpolación polinómica. Hay varias formas de implementarlo. Puede usar las fórmulas de interpolación de
Newton o
Lagrange , pero la forma más fácil de obtener el polinomio de interpolación es resolver un sistema de ecuaciones lineales.
Si un polinomio pasa por un punto, entonces obviamente podemos decir que
P (xi) = yi . Supongamos que queremos adaptar un polinomio a un conjunto de tres puntos. Esto significa que:

En el caso general, no podemos dibujar una línea a través de tres puntos arbitrarios. Y entonces tenemos que doblarlo, formando una parábola. O, en otras palabras, introduzca un polinomio de segundo grado, también conocido como función cuadrática.

Como se conocen xs e ys, solo necesitamos resolver el sistema y encontrar los coeficientes a, b, c, y dado que este sistema consta de tres ecuaciones y tres variables, generalmente podemos obtener una solución única.
Para asegurarse de esto, intente mover la posición de los tres puntos en la tabla inferior y vea qué sucede.

Este gráfico también es muy útil para el análisis mental de sistemas lineales. En el caso general, es imposible ajustar una línea recta en tres puntos, así como es imposible encontrar una solución para un sistema de n ecuaciones con n-1 variables desconocidas. Pero a veces es posible. Por ejemplo, en casos donde algunos de los puntos coinciden o todos ellos están ubicados intencionalmente en una línea recta.
La situación inversa es aún más interesante. Podemos dibujar un número infinito de parábolas a través de dos puntos dados. Todos ellos son igualmente adecuados como solución al problema. Y al mismo tiempo, no podemos obtener una solución excepcionalmente mejor para sistemas de n ecuaciones yn + 1 variables.
Pero, ¿y si todavía es posible? ¿Qué sucede si podemos introducir algún criterio adicional para elegir la opción más adecuada?
Síntesis
Preguntas similares nos llevan al territorio de la síntesis polinómica. En nuestro caso, este es un cruce entre series polinómicas y la interpolación polinómica. Usando series, podemos modelar una función basada en sus derivados en algún momento, y usando síntesis, podemos usar tanto puntos como derivados (y no solo ellos, sino más en otro momento).
La derivada de una función está estrechamente relacionada con las propiedades geométricas de su gráfico. La primera derivada determina la tangente de la pendiente de la tangente, y la segunda determina la curvatura.
Supongamos que necesitamos definir una función que pase por dos puntos, conociendo su tangente en ambos puntos. En este caso, podemos sintetizarlo fácilmente como un polinomio.
Como antes, necesitamos escribir un sistema de ecuaciones. Ahora necesitamos cuatro condiciones, por lo que debemos elegir un polinomio de grado 3, es decir, una función cúbica.
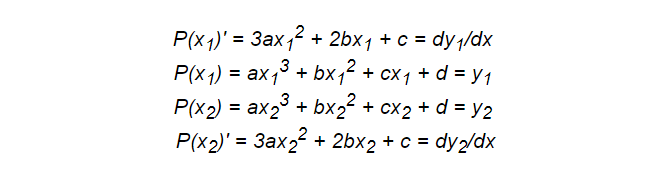
Algunas de las ecuaciones se basan en puntos, mientras que otras son derivadas. Las integrales también se pueden agregar aquí para introducir las propiedades enteras necesarias, lo que hace que esta técnica sea bastante efectiva.
Pero continuaremos considerando una función que conecte dos puntos de una línea suave continua con restricciones tangenciales en estos puntos.


Fenómeno Runge
La interpolación polinómica tiene una propiedad desagradable, que se manifiesta en un aumento en el crecimiento de las oscilaciones en ambos extremos del intervalo con un aumento en el número de puntos. Este fenómeno se llama fenómeno Runge. Limita la posibilidad de utilizar interpolaciones polinómicas simples.
Otro inconveniente de este enfoque es su naturaleza global, es decir, un cambio en toda la función junto con el más mínimo cambio en la posición de al menos un punto. En combinación con las oscilaciones, el resultado mismo es el caos.

Ganglios Chebyshev
Una de las formas de combatir el caos es seleccionar una malla especial para la interpolación: los
nodos de Chebyshev . Estos son valores especiales de x que se obtienen dividiendo un semicírculo con un radio de 1 en fragmentos iguales y proyectándolos en el eje x.
En general, una cierta magia matemática está oculta en esta técnica, pero desde un punto de vista pragmático, está destinada a minimizar el fenómeno Runge. Y aunque no permite que la interpolación sea completamente predecible, todo funciona de manera estable en el intervalo (-1: 1).

Por supuesto, puede extender el intervalo a lo largo del eje X tanto como lo necesite utilizando la transformación afín unidimensional. No es necesario adherirse al segmento
(-1; 1) .
Pero la interpolación al mismo tiempo conserva su ubicuidad. Cambiar el primer punto todavía afecta el funcionamiento de la función cerca del último, aunque no tan significativamente.
Splines
Existen bastantes variedades de splines, pero todas están unidas por un escenario de aplicación. Tan pronto como la interpolación global por alguna razón deje de ser adecuada para nuestras tareas, podemos dividir nuestro intervalo en fragmentos más pequeños y definir funciones individuales para la interpolación en cada una de ellas.
Lo único que debemos considerar es la necesidad de conectarlos en los extremos para mantener la continuidad. Si garantizamos la continuidad no solo de la función final definida por partes, sino también de su primera derivada, entonces, en este caso, las tangentes de cada uno de sus segmentos coincidirán y su programación se verá suave.
Hay una cierta
clasificación de splines. Por ejemplo, tome una spline polinómica que consta de dos fragmentos. Si cada fragmento está determinado por un polinomio de tercer grado, entonces se llama cúbico. Puede poseer, por ejemplo, una propiedad como la continuidad de la primera derivada, ya que las tangentes en la unión de los fragmentos coinciden. Sus fragmentos no son del mismo ancho. No es de origen natural, ya que podemos controlar derivados en sus extremos. Y, por supuesto, esta es una spline de interpolación, porque pasa exactamente a través de los puntos de cuadrícula que hemos indicado.

Conclusión
La probabilidad de que alguna vez tenga que poner en práctica su propia interpolación es extremadamente pequeña. Hay muchas soluciones listas para usar y, en la mayoría de los casos, solo tendrá que elegir la herramienta adecuada para el trabajo. Esta área de conocimiento no es tan complicada, pero la cantidad de palabras y nombres desconocidos puede alejarse.
El propósito de esta guía fue proporcionarle una comprensión básica de las ideas utilizadas para trabajar con polinomios y splines. En ningún caso pretende ser completo, porque de hecho, se escriben libros completos en cada uno de los pequeños capítulos de este material. Pero esperamos, al menos, que el enfoque interactivo de la presentación en este material sea útil no solo para una breve introducción, sino que si surge tal necesidad, lo ayudará a dominar temas más avanzados.
