Cosmología - Stanford. Resumen Conferencia 1

Este artículo abre una serie de apuntes sobre Cosmología de la Universidad de Stanford. Las conferencias en inglés están disponibles en: Cosmología (2013) - Leonard Susskind - Universidad de Stanford . Vi el video de la conferencia y describí con placer. El profesor Leonard Susskind explica muy accesible y divertido. Es evidente que es una persona talentosa y un excelente maestro.

La Universidad de Stanford también es famosa por el hecho de que nuestro destacado compatriota Andrei Linde trabaja allí, quien probablemente pronto recibirá el Premio Nobel de física por su contribución a la cosmología moderna. A quién le importa, te aconsejo que veas su conferencia pública Las muchas caras del universo .

Esta sinopsis es mi intento de autoeducación. Todavía lo escribiría para mí en un cuaderno. Pero decidí combinar negocios con placer. Espero que también sea interesante para alguien.

Inmediatamente haga una reserva que traté de tomar notas cerca del texto original. Sin embargo, en algunos lugares me permití complementar o generalizar las declaraciones del profesor basadas en mi propia experiencia como físico especialista. Esto se hizo únicamente para facilitar la comprensión, la comprensión y la asimilación del material.

En este artículo, se ofrece una sinopsis de la lección 1. Quizás una secuela aparezca más tarde.

Revisión histórica

La cosmología es un tema muy antiguo. La historia de la cosmología se remonta a miles de años. En particular, los antiguos griegos conocieron la cosmología durante mucho tiempo.

Estas conferencias cubren el período de tiempo no más allá de la segunda mitad del siglo XX, cuando Edwin Hubble descubrió la ley de expansión del universo.

Si hablamos de cosmología como ciencia, entonces este es un campo de conocimiento bastante nuevo. La cosmología moderna se remonta al descubrimiento de la radiación reliquia de microondas y la formulación de la teoría del big bang . Y esto solo sucedió en la década de 1960.

Hasta este punto, la cosmología no era una rama de la física, sino que pertenecía a las ciencias naturales. Es decir, en cosmología prevaleció el enfoque fenomenológico: observación, medición, clasificación, catalogación, etc.

En ese momento, la precisión de las mediciones era baja. Y por lo tanto, era imposible formular declaraciones exactas. Había ecuaciones, pero eran incorrectas e inexactas. Los físicos siempre han estado involucrados en el proceso de estudio, ya que las estrellas, galaxias y otros cuerpos celestes poseen características físicas como el momento angular, por ejemplo. Los químicos físicos también estuvieron involucrados, ya que los cuerpos celestes tienen una composición química.

Sin embargo, la actitud hacia el Universo en sí como un objeto físico, el Universo como un sistema que debe estudiarse matemáticamente utilizando un conjunto de principios físicos y las ecuaciones correctas exactas correspondientes: este es un enfoque relativamente joven.

Propiedades del universo

En estas conferencias, el Universo se considera como un sistema físico. Y lo estudiaremos usando ecuaciones. Podemos comenzar nuestra exploración del universo con algunas observaciones generales.

Isotropía

Entonces, la primera observación, que, en términos generales, puede no ser absolutamente precisa, al igual que toda la física no es absolutamente exacta, es que el Universo es isotrópico .

Isotropía significa que el universo se ve igual en cualquier dirección. Por supuesto, esto es cierto solo para distancias suficientemente grandes. Si miras demasiado de cerca, entonces la isotropía puede no observarse debido a las inhomogeneidades locales, por ejemplo, debido a la forma de nuestra galaxia.

Uniformidad

Si el Universo es isotrópico, entonces se puede argumentar con gran certeza que el Universo también debe ser homogéneo . La homogeneidad no significa uniformidad en todas las direcciones, sino en todos los lugares. Es decir, a gran escala, el Universo se ve igual independientemente de dónde se encuentre el observador: en nuestra galaxia o en alguna otra, que está muy, muy lejos de nosotros.

Galaxias

Las galaxias en la escala del Universo son efectivamente puntos de concentración de masa . Podemos tratarlos como puntos materiales. El número aproximado de galaxias en la parte visible del universo es cien mil millones $$$10 ^ {11} = 100 \, 000 \, 000 \, $ 00$ . A su vez, cada galaxia también contiene aproximadamente $$$10 ^ {11}$ cien mil millones de estrellas. Debemos recordar que este es el número de galaxias que solo podemos ver dentro de la esfera. Solo hasta donde los astrónomos pueden ver con telescopios. Es decir, lo más lejos que podemos ver es a una distancia desde donde la luz logró alcanzarnos a lo largo de toda la existencia del Universo: alrededor de 13 mil millones de años.

Un hecho interesante El número total de estrellas en la parte visible del universo. $$$10 ^ {11} \ cdot 10 ^ {11} = 10 ^ {22}$ , y si cada estrella tiene un promedio de 10 planetas, entonces resulta $$$10 ^ {23}$ - el número de planetas de Avogadro en el universo. Topo planetario de la sustancia! (profesor ríe)

Un argumento en contra de la homogeneidad del universo. Refutación

Considere una parte del universo donde estamos. Lo sabemos con certeza, porque vemos que el Universo es isotrópico . Suponemos que el universo también es homogéneo . Pero, ¿qué pasaría si el universo no fuera homogéneo?

Si el Universo es isotrópico, entonces la única forma de que no sea homogéneo es tener una estructura en forma de conchas.


La hipótesis de un universo heterogéneo. A la izquierda hay un Universo isotrópico homogéneo; a la derecha hay un Universo isotrópico no homogéneo. La cruz en el centro nos denota.

Si esto fuera así, entonces, en cualquier otro punto, el Universo no se vería isotrópico. Es decir, si no queremos creer que de alguna manera estábamos exactamente en el centro del Universo, y que todo el Universo tiene una simetría esférica a nuestro alrededor, entonces tendremos que admitir que el Universo no solo es isotrópico, sino también homogéneo.

Principio cosmologico

Entonces, si no creemos que estamos ubicados exactamente en el centro del Universo, entonces el Universo debe ser homogéneo. Un universo homogéneo significa que el universo está uniformemente lleno de partículas (galaxias) en todo el volumen. Esto se llama el principio cosmológico . El principio cosmológico es cierto, porque nuestras observaciones indican esto, por supuesto, hasta cierto punto de aproximación.

Algunos astrónomos afirman que observaron heterogeneidades a gran escala en el universo. El profesor duda de la fiabilidad de estas fuentes y declaraciones.

Por supuesto, la idea de la homogeneidad del universo no es absolutamente precisa. Incluso el hecho de que existan galaxias ya sugiere que hay heterogeneidades. Por cierto, no solo hay galaxias sino también cúmulos de galaxias. Sin embargo, en una escala bastante grande, aproximadamente del orden de mil millones de años luz, el Universo parece homogéneo.

Al principio, el principio cosmológico era solo un postulado. Pero con la acumulación de datos de observación, se confirmó de manera cada vez más confiable y, al final, se descubrió la radiación reliquia de microondas, lo que indica que la distribución inicial de la materia en el Universo fue muy homogénea.

Declaración del problema físico.

Hay un gas uniforme de partículas galácticas. Y cada galaxia interactúa con otras galaxias. Las galaxias en su conjunto son eléctricamente neutras. Pero no son neutrales gravitacionalmente. Interactúan a través de la gravedad newtoniana. Y esta es la única fuerza importante a gran escala. La gravedad actúa sobre las galaxias e intenta unirlas a todas.

Entonces, si observas cualquier punto del Universo y te preguntas dónde debería moverse, puedes adivinar que desde todos los lados está rodeado por la misma cantidad de masa. Siguiendo esta lógica, se puede suponer que ninguna galaxia debería moverse en absoluto, y el Universo debería ser estático, ya que el resultado de las fuerzas que actúan en cualquier punto del Universo es cero. ¡Esto está absolutamente mal!

Y ahora tenemos ecuaciones de movimiento newtonianas para el universo. Es posible que haya escuchado que el universo en expansión está en buen acuerdo con la teoría general de la relatividad de Einstein, y que antes de la teoría general de la relatividad, la ley del universo en expansión era incomprensible. Esto simplemente no es cierto. Quizás esto fue tan históricamente. Pero esto es solo un hecho histórico sobre las fechas, no sobre la lógica. Newton podría obtener las ecuaciones de un universo en expansión. Y ahora lo haremos como Newton debería haberlo hecho.

Sistema de coordenadas

En cualquier problema físico, lo primero que debe hacer es introducir un sistema de coordenadas. En lugar de elegir el escalón de la cuadrícula como una distancia: 1 metro, un millón de kilómetros, mil años luz, elegiremos una cuadrícula para que sus nodos se unan rígidamente a las galaxias. Como el universo es homogéneo, podemos hacerlo. Entonces las galaxias siempre permanecerán aproximadamente en las mismas coordenadas, independientemente de lo que le ocurra al universo. Es decir, las galaxias parecen estar "congeladas" en la cuadrícula de coordenadas.

No es del todo obvio que esto se pueda hacer. Si las galaxias se movieron completamente por accidente y en direcciones completamente diferentes, entonces no podríamos hacer esto. Pero vemos que las galaxias se mueven por casualidad. Vemos que las galaxias se mueven en concierto, exactamente como si estuvieran incrustadas en una determinada cuadrícula de coordenadas. Y lo que vemos nos permite hacer esto, porque las velocidades de las galaxias entre sí son consistentes y no accidentales.

Introducimos una cuadrícula $$$(x, y, z)$ . Estas coordenadas no se miden en unidades de longitud. Si consideramos dos galaxias separadas por un intervalo $$$\ Delta x$ entonces la distancia $$$D$ entre ellos (en metros) se expresa como

$$

$$D = a \, \ Delta x$$

donde $$$a$ Es un parámetro de escala, que puede ser una constante, pero en general, puede no serlo. El parámetro de escala puede depender del tiempo. $$$a = a (t)$ .

Por lo tanto, según el teorema de Pitágoras, la distancia entre dos galaxias generalmente se escribe como

$$

$$D = a (t) \ sqrt {\ Delta x ^ 2 + \ Delta y ^ 2 + \ Delta z ^ 2}$$

Y por supuesto, el parámetro $$$a$ No es una constante. Si fuera una constante, entonces las galaxias serían estáticas, no se moverían a ningún lado. Y esto no es lo que estamos observando. Vemos que vuelan aparte.

Ley de Hubble

Escribimos la velocidad relativa entre dos galaxias. Diferenciamos la fórmula anterior en el tiempo. Tenemos en cuenta que $$$\ Delta x$ - Este es un intervalo fijo, que no se puede cambiar de acuerdo con las condiciones para construir un sistema de coordenadas. Entonces

$$

$$\ mathcal {V} = \ dot {a} \, \ Delta x$$

donde usamos la notación $$$\ dot {a} = da / dt$ .

Ahora escribimos la relación entre la velocidad relativa de dos galaxias y la distancia entre ellas.

$$

$$\ frac {\ mathcal {V}} {D} = \ frac {\ dot {a} (t)} {a (t)}$$

Tenga en cuenta que $$$\ Delta x$ se reduce, y esta relación no depende en absoluto de las coordenadas. Es decir, esta fórmula es válida para dos galaxias, sin importar cuán lejos o cerca estén.

Esta relación se llama parámetro constante de Hubble.

$$

$$H (t) = \ frac {\ dot {a} (t)} {a (t)}$$

y no depende de las coordenadas. Entonces puedes escribir lo mismo en forma estándar

$$

$$\ mathcal {V} = H \, D$$

La velocidad relativa de dos galaxias es proporcional a la distancia entre ellas.

Debe comprender que nunca lo habríamos escrito si Hubble no hubiera descubierto su ley. La ley de Hubble, por otro lado, no es tan sorprendente. Hay un dicho: "No es sorprendente que el caballo más rápido cabalgue por delante de todos". Cuanto más rápido te muevas, más lejos estarás. Y este es un hecho que Hubble descubrió.

Masa de materia en el universo

Considera un poco de volumen $$$\ Delta x \, \ Delta y \, \ Delta z$ . Hacemos una pregunta: ¿qué masa se concentra en este volumen? Dejar $$$\ nu$ Es la masa de una sustancia en un volumen elemental. $$$dx \, dy \, dz$ (en kilogramos) Entonces la masa en volumen $$$\ Delta x \, \ Delta y \, \ Delta z$ es igual a

$$

$$M = \ nu \, \ Delta x \, \ Delta y \, \ Delta z$$

¿Cuál es el volumen métrico de esta área? Desde $$$D = a \, \ Delta x$ podemos escribir

$$

$$V = a ^ 3 \, \ Delta x \, \ Delta y \, \ Delta z$$

¿Cuál es la densidad de la sustancia en esta área? Por definición, la densidad es $$$\ rho = M / V$ , es decir, teniendo en cuenta las dos fórmulas anteriores, obtenemos

$$

$$\ rho = \ frac {\ nu} {a ^ 3}$$

Esta es la densidad física estándar de una sustancia.

Aunque la cantidad total de masa en volumen $$$\ Delta x \, \ Delta y \, \ Delta z$ no cambia, ya que las galaxias están "congeladas" en la cuadrícula de coordenadas, la densidad absoluta de la materia en el mismo volumen puede cambiar, ya que el parámetro $$$a (t)$ depende del tiempo

Teorema de Newton

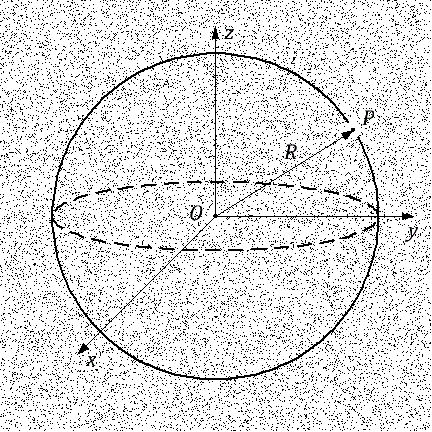Ilustración del teorema de Newton

Considere dos galactiti. Siempre podemos poner uno de ellos en el origen. Deja que la galaxia $$$O$ está en el origen, y la galaxia $$$P$ está a cierta distancia de ella.

El teorema de Newton establece que la fuerza de gravedad que actúa sobre una galaxia $$$P$ depende solo de la cantidad de masa dentro de la esfera centrada en el origen $$$O$ y pasando por la galaxia $$$P$ . La segunda afirmación del teorema de Newton es que toda la masa dentro de esta esfera puede considerarse concentrada en el centro en el origen en el punto $$$O$ , siempre que la masa dentro de la esfera se distribuya, si no de manera uniforme, al menos isotrópicamente .

En otras palabras, el efecto de toda la masa dentro de la esfera en la galaxia $$$P$ equivalente a como si esta masa se concentrara en un solo punto $$$O$ , que es el centro de la esfera.

Ecuaciones de movimiento newtonianas

Encuentra la distancia entre galaxias $$$P$ y $$$O$ . Galaxia $$$P$ tiene coordenadas $$$(x, y, z)$ , es decir, la distancia desde el centro a la galaxia $$$P$ es igual

$$

$$D = a (t) \ sqrt {x ^ 2 + y ^ 2 + z ^ 2}$$

Podemos introducir la notación

$$

$$R = \ sqrt {x ^ 2 + y ^ 2 + z ^ 2}$$

$$$R$ no medido en metros, pero en las mismas unidades que $$$x$ , $$$y$ y $$$z$ y no depende del tiempo Entonces

$$

$$D = a (t) \, R$$

Ahora registramos la velocidad y la aceleración de la galaxia. $$$P$

$$

$$\ mathcal {V} = \ dot {a} (t) \, R$$

$$

$$\ mathcal {A} = \ ddot {a} (t) \, R$$

Ahora tenemos que equiparar la aceleración $$$\ mathcal {A}$ a la aceleración asociada con toda la masa gravitante dentro de una esfera de radio $$$R$ . Denota la masa de la galaxia $$$P$ para $$$m$ , y la masa de toda la materia dentro de la esfera más allá $$$M$ . Entonces la fuerza de gravedad que actúa sobre la galaxia $$$P$ es igual a

$$

$$F = -G \ frac {m \, M} {D ^ 2}$$

donde $$$G = 6.67408 \ times10 ^ {- 11} \ mathrm {N \ cdot m ^ 2 \ cdot kg ^ {- 2}}$ - constante gravitacional. El signo menos en la fórmula significa que es una fuerza atractiva.

Ahora puedes grabar la aceleración de la galaxia $$$P$

$$

$$\ mathcal {A} = -G \ frac {M} {D ^ 2}$$

Igualamos dos expresiones para $$$\ mathcal {A}$ y obtener

$$

$$\ ddot {a} (t) \, R = -G \ frac {M} {D ^ 2}$$

Tenemos en cuenta que $$$D = a \, R$ entonces

$$

$$\ ddot {a} \, R = - \ frac {M \, G} {a ^ 2 \, R ^ 2}$$

Divide ambos lados entre $$$a \, R$

$$

$$\ frac {\ ddot {a}} {a} = - \ frac {M \, G} {a ^ 3 \, R ^ 3}$$

Encuentra el volumen de la esfera

$$

$$V = \ frac {4} {3} \ pi \, D ^ 3 = \ frac {4} {3} \ pi \, a ^ 3 \, R ^ 3$$

Multiplicamos el numerador y el denominador del lado derecho por $$$4 \ pi / 3$

$$

$$\ frac {\ ddot {a}} {a} = - \ frac {4} {3} \ pi \, G \, \ rho$$

Esta ecuación es independiente de $$$R$ , y es cierto para cualquier galaxia en el universo. Esta ecuación es la ecuación fundamental central de la cosmología .

Una de las consecuencias de esta ecuación es que es imposible que el Universo sea estático si no está vacío. De esta ecuación se deduce que el Universo puede ser estático solo si está vacío.

Podemos reescribir esta ecuación, dado que $$$\ rho = \ nu / a ^ 3$

$$

$$\ frac {\ ddot {a}} {a} = - \ frac {4 \ pi} {3} \ frac {G \, \ nu} {a ^ 3}$$

Esta ecuación se obtuvo por primera vez en el contexto de la teoría general de la relatividad de Alexander Friedman. Esta ecuación no nos dice si el universo se está expandiendo o contrayendo. Solo dice que la segunda derivada del factor de escala es negativa. Es decir, si el Universo se expande, entonces se ralentiza, y si el Universo se contrae, entonces se acelera.

De hecho, el universo se está expandiendo y no se está desacelerando. Acabamos de hacer lo que Newton podía hacer y que todos los cosmólogos consideraron correcto hasta aproximadamente 1998. Este modelo fue generalmente aceptado y se llamó el modelo estándar del Universo hasta que se descubrió abiertamente la expansión acelerada del Universo. Hasta ahora, el lado derecho de la ecuación tiene solo un término. De hecho, debería haber varios términos relacionados con la teoría general de la relatividad.

Velocidad de salida

Ahora escribe toda la energía de la galaxia $$$P$ como la suma de la cinética y el potencial

$$

$$E = \ frac {1} {2} m \ matemática {V} ^ 2 - G \ frac {m \, M} {D}$$

La energía puede ser positiva o negativa dependiendo de la relación entre estos dos términos. También es importante recordar que la energía total de la partícula $$$P$ guardado Si la energía total es positiva, entonces la partícula no puede regresar. Una partícula regresa solo cuando la energía total es negativa. El caso límite es que la energía total es cero. Resuelve la ecuación $$$E = 0$ para $$$\ mathcal {V}$ para encontrar la velocidad de salida.

$$

$$\ frac {1} {2} m \ matemática {V} ^ 2 - G \ frac {m \, M} {D} = 0$$

$$

$$\ mathcal {V} _ {0} = \ frac {2MG} {D}$$

Como una galaxia $$$P$ todo el Universo puede tener una velocidad mayor que la velocidad de salida, menor que la velocidad de salida o igual a la velocidad de salida. Si la velocidad del Universo es mayor que la velocidad de partida, entonces se expande y nunca comienza a reducirse; si el Universo tiene una velocidad inferior a la velocidad de partida, tarde o temprano comenzará a reducirse.

Reescribe la ecuación de energía total

$$

$$\ frac {1} {2} m \, \ dot {a} ^ 2 R ^ 2 - \ frac {m \, MG} {aR} = E$$

Ecuación de Friedman

Considere el caso cuando la velocidad del universo coincide con la velocidad de partida.

$$

$$\ frac {1} {2} m \, \ dot {a} ^ 2 R ^ 2 - \ frac {m \, MG} {aR} = 0$$

Simplifica la expresión: divide por $$$m$ , multiplicar por 2, dividir por $$$a ^ 2 R ^ 2$

$$

$$\ frac {\ dot {a} ^ 2} {a ^ 2} - \ frac {2MG} {a ^ 3R ^ 3} = 0$$

En el segundo término, multiplicamos el numerador y el denominador por $$$4 \ pi / 3$ . Luego en el denominador obtenemos el volumen métrico de la esfera $$$V$ . Dado que $$$M / V = ​​\ rho$ tenemos

$$

$$\ left (\ frac {\ dot {a}} {a} \ right) ^ 2 = \ frac {8 \ pi} {3} G \ rho$$

Esto se llama la ecuación de Friedman . Es equivalente a la ecuación newtoniana obtenida anteriormente. Como asumimos que la energía total es cero, dicho universo se expande, disminuyendo asintóticamente a cero, pero nunca cruza cero y no comienza a reducirse.

Recordemos ahora que $$$\ rho = \ nu / a ^ 3$ . Reescribe la ecuación de Friedman

$$

$$\ left (\ frac {\ dot {a}} {a} \ right) ^ 2 = \ frac {8 \ pi} {3} \ frac {\ nu G} {a ^ 3}$$

Parámetro $$$\ nu$ muy flexibleDepende completamente de nuestra elección de la cuadrícula. Y en términos generales, incluso podríamos elegirlo para que$$$\frac{8\pi}{3}\nu G = 1$ . Entonces

$$

$$\left(\frac{\dot{a}}{a}\right)^2 = \frac{1}{a^3}$$

El lado derecho de esta ecuación siempre es positivo y, por lo tanto, la tasa de expansión
$$$\dot{a}$nunca se vuelve cero Recordemos ahora que$$$\dot{a}/a = H$Es un parámetro constante de Hubble. También se deduce de la ecuación que el parámetro Hubble nunca cambia de signo. Sin embargo, todavía se está desacelerando. El parámetro Hubble se vuelve cada vez menos con el tiempo.

Esta ecuación es extremadamente importante para toda cosmología. Una manera simple de resolverlo es buscar una solución de cierto tipo, es decir, buscaremos una solución en la forma

$$

$$a(t) = c\,t^p$$

donde $$$c$ y $$$p$ - Algunas constantes.

$$

$$\dot{a} = c\,p\,t^{p-1}$$

$$

$$\frac{\dot{a}^2}{a^2} = \frac{p^2}{t^2}$$

$$

$$\frac{p^2}{t^2} = \frac{1}{c^3\,t^{3p}}$$

$$

$$3p = 2\\ p^2 = \frac{1}{c^3}$$

$$

$$p = \frac{2}{3}\\ c = \left(\frac{3}{2}\right)^{\frac{2}{3}}$$

Hemos obtenido una solución a la ecuación de Friedman.


Gráfico de la solución de la ecuación de Friedman.

El Universo real sigue esta decisión solo hasta cierto punto en el tiempo, y luego comienza a acelerarse. Newton podría hacer esto. Se acercó mucho. Hice todas las preguntas correctas. El profesor confía en que Newton, muy probablemente, hizo esto y recibió esta decisión. Sin embargo, dicha información sobre el universo era contraria a sus puntos de vista religiosos y, por lo tanto, no publicó sus descubrimientos.