Hola geektimes
En el proceso de inactividad, surgió la idea de estudiar varios juegos de azar, al mismo tiempo para comprender mejor cómo funciona. Los resultados, aunque generalmente obvios, fueron lo suficientemente interesantes como para compartirlos con el público.
Para quien los detalles son interesantes, pregunto bajo cat.
Dados: Juego de dados
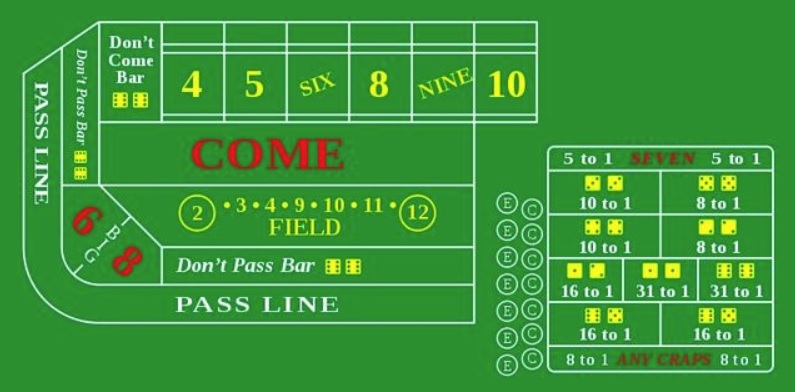
Lo más probable es que sea una opción intuitivamente simple y comprensible: hay un cubo con marcas del 1 al 6, y la probabilidad de que un número en particular se caiga es 1/6. Pero jugar de esta manera sería aburrido, por lo que los juegos con reglas más complejas son populares. Un juego de azar popular son los
dados , la imagen de arriba muestra una imagen de la mesa de juego. Como puede ver, hay mucho de todo, pero no entraremos en sutilezas profundas.
Cada turno del juego consiste en lanzar dos dados, los puntos acumulados se suman. Como
dice el
artículo , “Las reglas del juego son sencillas: un jugador tira dos dados, y si la suma de puntos en ellos es 7 u 11, gana, si 2, 3 o 12, pierde. Cuando una cantidad diferente cae en los dados, el tirador los lanza a una combinación ganadora o perdedora ”.
Veamos cuánto puedes ganar de esta manera. No es necesario ir a un casino para esto; usaremos Python para simular el juego. Escribimos una función para un tiro:
import random def shoot(): return random.randint(1,6) + random.randint(1,6)
Escribiremos la función de simulación de un movimiento de acuerdo con las reglas anteriores.
def move(): while True: val = shoot() print "Dice roll:", val if val == 7 or val == 11: return True if val == 2 or val == 3 or val == 12: return False
Configuremos a nuestro jugador virtual una cantidad inicial de $ 100 y comencemos el proceso del juego. Deje que nuestro jugador haga 100 apuestas, cada vez 1u.e.
money_total = 100 win = 0 loss = 0 for p in range(100): bet = 1 step = move() if step is True: money_total += bet win += 1 else: money_total -= bet loss += 1 print "Win", win, "Loss", loss, "Money", money_total
Comenzamos la simulación de 100 juegos y estamos sorprendidos por el resultado, el jugador
ganó y con un margen notable de victorias de las derrotas: Ganar 63, Perder 37, Dinero 126. Aumentamos el número de juegos a 1000 y corremos nuevamente, el jugador ganó nuevamente: Ganó 680, Pérdida 320, Dinero 460 .
Está claro que algo está mal aquí: un juego en el que el jugador siempre estaría en negro, difícilmente sería popular en el casino, simplemente iría a la quiebra. Tratemos de resolverlo.
Parece intuitivamente que al lanzar un dado, la probabilidad de que se caiga cualquier faceta es igualmente probable. Y esto es cierto, pero en el caso de
un cubo. Si hay dos cubos, entonces todo se vuelve más complicado. Por ejemplo, el número 7 puede salir como 3 + 4, 2 + 5, 1 + 6, pero el número 12 puede caer solo como una combinación de 6 + 6.
En el cuaderno Jupyter construimos un cronograma para la pérdida de cantidades del 1 al 12 por 100 lanzamientos:
from matplotlib import pyplot as plt %matplotlib inline y = [ shoot() for v in range(100) ] plt.hist(y)
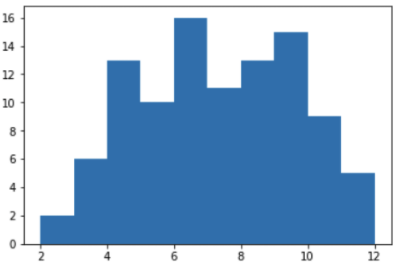
La suposición se confirmó, y la cantidad del centro realmente se cae más a menudo. Por lo tanto, los números 7 y 11 realmente se caen con más frecuencia que 2.3 o 12. Y la probabilidad de obtener una combinación ganadora "7 u 11" es realmente mayor.
¿Cómo puede ser esto? Lamentablemente, la respuesta es simple: el autor del artículo citado anteriormente simplemente no entendió completamente las reglas del juego. El texto "las
reglas del juego son sencillas: el jugador tira dos dados, y si la suma de puntos en ellos es 7 u 11, gana, si 2, 3 o 12 - pierde " está muy lejos de la verdad, y las reglas en los dados no son tan sencillas como parecen .
Las reglas reales para apostar en la línea de pase resultaron ser un poco más complicadas (hay otros tipos de apuestas, aquellos que lo deseen pueden resolverlo por su cuenta).
Mover 1 : se hace una tirada. Si cae 7 u 11, el jugador gana; si 2, 3 o 12, el jugador pierde. Si se cae otro número, se recuerda debajo del punto del nombre.
Movimiento 2 : se hace una tirada. Si 7 cae, entonces el jugador pierde. Si el punto cae, entonces el jugador ganó. Si otros números caen, el movimiento se repite (en este momento, los jugadores también pueden apostar a otros números).
De hecho, todo es un poco más complicado de lo que se describe en la versión original. Agregamos una función de simulación teniendo en cuenta reglas más precisas.
def move(): point = 0 while True: val = shoot() if point == 0:
El resultado ahora es más similar a la verdad: para 100 juegos, el jugador ganó 43 veces, perdió 57 veces, el saldo al final del juego fue de 86.u. del original 100. También es interesante que el número de victorias resultó ser bastante grande, y es solo un poco menos del 50%. Esta es una estrategia competente desde el punto de vista del casino: le permite mantener el interés del participante en el juego (no sería interesante perder todo el tiempo), pero al mismo tiempo, el saldo de ganancias del casino sigue siendo positivo y el saldo monetario del jugador es en consecuencia negativo.
Veamos con más detalle lo que se obtiene para la simulación de 100 juegos.
- La posibilidad de ganar en el primer paso cayó en unos 20 casos.
- La posibilidad de perder inmediatamente en el primer paso cayó en 15 casos.
- En los 65 casos restantes, el juego continúa, y todo es complicado: la elección proviene de dos números, 7 y puntos, pero como se puede ver en el gráfico anterior, la probabilidad de que un número 7 "perdedor" se caiga es máxima, lo que en general se demostró.
Es interesante notar que la posibilidad de ganar al 45% es bastante alta. Entonces, ¿es posible ganar? En el corto plazo, por ejemplo, en otra simulación, el jugador tuvo "suerte", y en 100 juegos aumentó su capital virtual de 100 a 112ye.
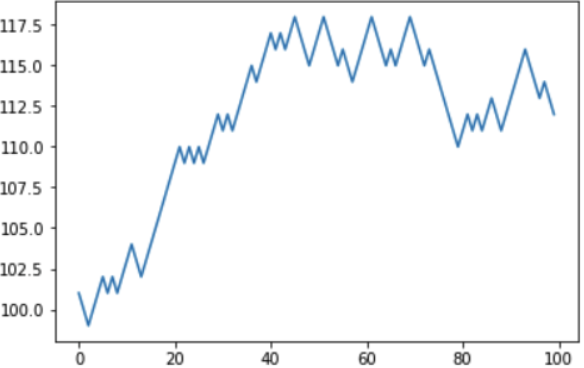
Pero ya la próxima simulación mostró un balance negativo: el jugador redujo su estado de 100 a 88 años, habiendo perdido, por cierto, el mismo 12 años "ganado" la vez anterior.
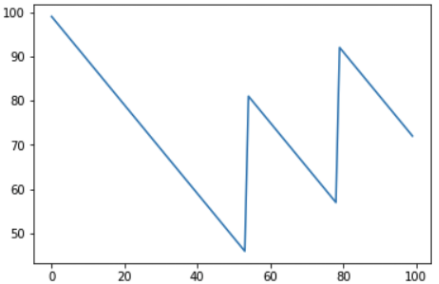
Si aumenta el número de iteraciones a 1000, puede ver cómo se verá el saldo monetario del jugador a largo plazo:
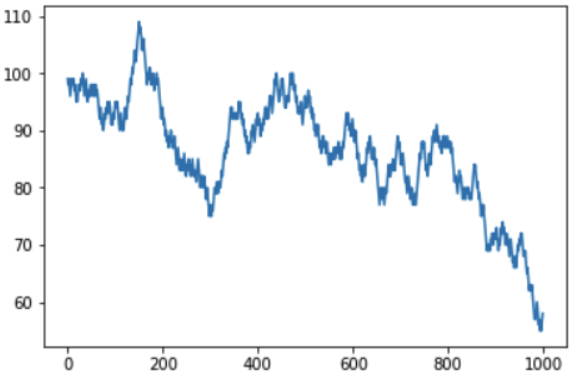
Está claro que con una posibilidad de ganar cada juego menos del 50%, la cantidad de dinero resultante en la cuenta del jugador disminuirá gradualmente, y la cantidad de ganancias del casino aumentará gradualmente. En la tabla, por cierto, las explosiones y caídas son visibles, y puede surgir una pregunta razonable: ¿pueden predecirse? Ay, no, porque Las tiradas de dados son eventos independientes entre sí, y los resultados anteriores no afectan lo siguiente de ninguna manera. Puede repetir la idea principal una vez más: puede ganar una o incluso varias veces, pero a la larga es imposible mantenerse en el plus en el casino, las reglas del juego están redactadas para que el saldo no sea a favor del jugador.
Hay otros tipos de apuestas en el juego de dados, y aquellos que lo deseen pueden analizarlas por su cuenta.
Ruleta americana
El siguiente tipo popular de juego es la ruleta, considere su versión estadounidense.
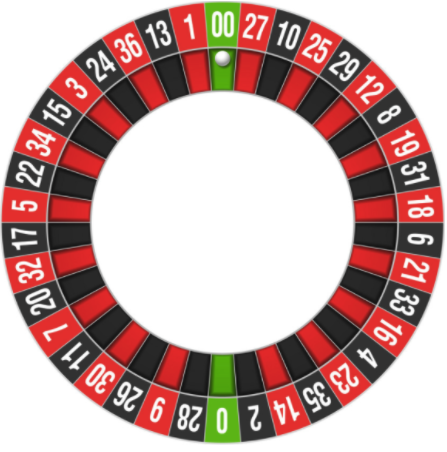
El campo de juego de la ruleta se divide en 38 celdas: 36 zonas con números + 2 zonas "cero" y "doble cero". Una pelota lanzada a una ruleta obviamente se detendrá en una de las zonas. El jugador puede hacer una variedad de apuestas, de las cuales hay más de 10 tipos, considere algunas de ellas.
Negro-rojo (o par-impar)Un jugador gana si la apuesta que nombra coincide. Obviamente, la probabilidad de negro o rojo sería 50/50, si no fuera por dos campos de cero, si los golpean, la apuesta pierde. Como en el caso de los dados, esto hace que la probabilidad de ganar sea solo un poco menos del 50%, pero esto "ligeramente" es suficiente para estar en números rojos.
Escribiremos la función de simular el movimiento usando números aleatorios del 1 al 38, los últimos 2 dígitos serán considerados como "cero".
def move_roulette1(): val = random.randint(1,38) if val == 37 or val == 38: return False return val % 2 != 0
Ejecute la simulación para 100 juegos, el código es el mismo que en la simulación de dados, solo cambiamos la llamada a la función.
money_total = 100 win = 0 loss = 0 for p in range(100): bet = 1 step = move_roulette1() if step is True: money_total += bet win += 1 else: money_total -= bet loss += 1 print "Win", win, "Loss", loss, "Money", money_total
Resultado: en 100 intentos, el jugador ganó 46 veces y perdió 54 veces. El gráfico muestra que el jugador tuvo "subidas" y "caídas", pero el saldo final sigue siendo negativo.
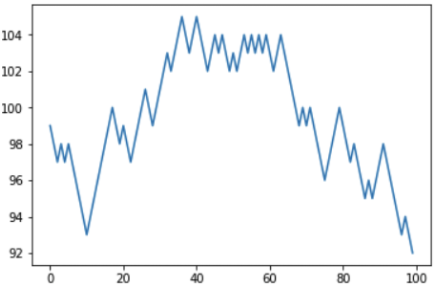
Cuanto más jugamos, más profundizamos en menos, y el casino, respectivamente, en más:
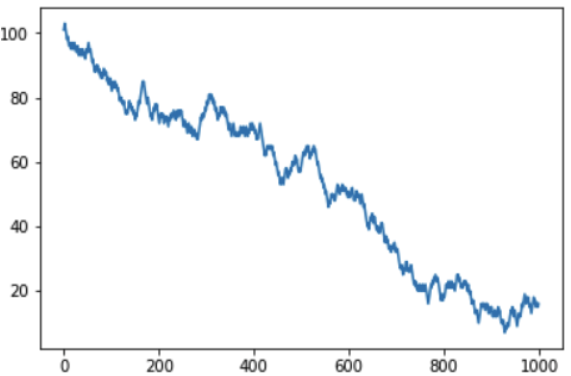
Hubo una pregunta del lector por qué no consideraba la ruleta europea con un campo "cero". Como puede suponer, la posibilidad de ganar allí es realmente mayor, pero el principio general no cambia. De hecho, la diferencia está solo en la "pérdida de velocidad". Aquí está el calendario conjunto para las versiones estadounidense y europea del juego:
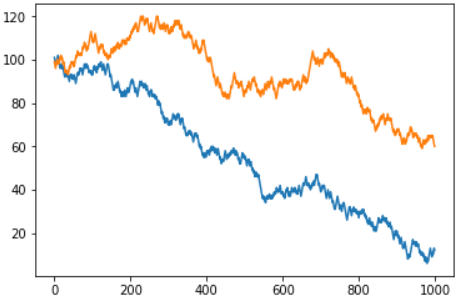
Aquellos que quieran probar la versión europea de la ruleta con 37 máquinas tragamonedas pueden usar la segunda opción de la función:
def move_roulette1(): val = random.randint(1,37) if val == 37: return False return val % 2 != 0
Apuesta por un número específicoEl jugador también puede apostar en un cierto número, la apuesta para ganar es 35: 1. Parece genial, pero es fácil adivinar que la probabilidad de que se caiga cierto número de ruleta es 1:38, es decir de nuevo, un poco menos.
Agreguemos la función de apuesta a un número específico:
def move_roulette2(num): val = random.randint(1,38) return val == num
Simulación, suponemos que el jugador pone el número 10:
money_total = 100 win = 0 loss = 0 for p in range(100): bet = 1 step = move_roulette2(10) if step is True: money_total += 35*bet win += 1 else: money_total -= bet loss += 1 print "Win", win, "Loss", loss, "Money", money_total
Como resultado, el jugador ganó 2 veces y perdió 98 veces, el saldo final es -28.u.
 Apuesta por dos números
Apuesta por dos númerosPuede apostar en dos números: la posibilidad de ganar es mayor, pero la apuesta es menor y es 17: 1.
Escribamos una función:
def move_roulette3(num1, num2): val = random.randint(1,38) return val == num1 or val == num2
Para 100 intentos de nuestra simulación, el jugador ganó 3 veces y perdió 97 veces, el saldo fue -46u.e.
Hay otros tipos de apuestas, por ejemplo, para 4 números con un coeficiente de 1: 8, aquellos que lo deseen pueden experimentar por su cuenta. Como puede suponer, todas las probabilidades están diseñadas para que el jugador esté en rojo. Parece tentador poner 1ye en el número para ganar hasta 35ue. Pero la cantidad ganadora aumenta en 35 veces, y la posibilidad de ganar disminuye en 38 veces: el saldo final seguirá siendo favorable para el casino.
Lotto 6 de 45
Lo siguiente que es interesante verificar es la lotería. El principio del juego es bastante simple: hay 45 bolas en el tambor, 6 de ellas caen al azar. El precio del boleto según el sitio web de Gosloto es de 100 rublos, y el premio depende del número de bolas adivinadas. El orden aproximado de las ganancias es el siguiente: 2 bolas adivinadas dan una ganancia de 100r, 3 bolas adivinadas dan 300r, 4 bolas - 3000r, 5 bolas - 300.000r y 6 bolas - un super premio de aproximadamente 10.000.000r.
Primero, escriba un programa para lanzar bolas y comparar el resultado:
def lottery(values): balls = range(1, 45+1) b1 = balls.pop(random.randint(0, len(balls)-1)) b2 = balls.pop(random.randint(0, len(balls)-1)) b3 = balls.pop(random.randint(0, len(balls)-1)) b4 = balls.pop(random.randint(0, len(balls)-1)) b5 = balls.pop(random.randint(0, len(balls)-1)) b6 = balls.pop(random.randint(0, len(balls)-1)) s = [b1,b2,b3,b4,b5,b6] res = list(set(s) & set(values)) return len(res)
Una bola aleatoria "obtiene" 6 veces del conjunto de bolas, luego se determina el número de elementos de intersección de dos conjuntos. Ahora construiremos un gráfico de la ganancia total en la cantidad de boletos comprados. Por simplicidad, suponemos que el jugador apuesta por los mismos números.
money = [] money_total = 0 ticket_price = 100 for p in xrange(N): val = lottery([3,7,12,18,33,28]) if val == 2: money_total += 100 if val == 3: money_total += 300 if val == 4: money_total += 3000 if val == 5: money_total += 300000 if val == 6: money_total += 10000000 money.append(money_total) x = range(0, N) price = map(lambda x: ticket_price*x, x) from matplotlib import pyplot as plt %matplotlib inline plt.plot(price, money)
Para comprender el orden de magnitud: si compra 100 boletos (el monto total gastado será de 10.000 r), esto le dará 14 bolas "dobles" adivinadas y una "triple" adivinada. La ganancia total es de aproximadamente 2000r con 10,000r gastados.
El calendario de pagos para la cantidad gastada es casi lineal:

Resulta que si compras boletos en un millón, la ganancia será de 250 mil. El "super premio" en la simulación nunca se cayó, aunque en teoría, ciertamente es posible. Por cierto, como está escrito en las reglas, el premio total es el 50% de las entradas vendidas, pero el "super premio" no siempre se cae, por lo que con el casino, los organizadores, por supuesto, siempre ganan.
Máquinas tragamonedas
También trabajan en un principio (pseudo) aleatorio, "pseudo" porque El código en ellos ha sido durante mucho tiempo programático y no tiene una mecánica limpia. Los principios generales descritos anteriormente para las máquinas tragamonedas también funcionan, y los gráficos probablemente no serán diferentes, aquellos que lo deseen pueden agregar la función de simulación por su cuenta.
Un buen artículo sobre el diseño de máquinas de juego ya ha estado en Geektimes.
Conclusión
Quizás este artículo no abrió Estados Unidos a muchos, pero en los gráficos es, en principio, más visual. Resultó ser más interesante comparar un enfoque psicológico fundamentalmente diferente del juego. Las ganancias en la lotería son potencialmente grandes, pero muy raras. En los casinos, el enfoque es el opuesto: las apuestas se configuran para que una persona gane con la mayor frecuencia posible. Condicionalmente, después de haber realizado 10 juegos en un casino, una persona ganará 4 veces y perderá 6 veces. Esto permite que el jugador no pierda interés en el juego, pero en cualquier caso, el saldo general sigue siendo negativo: una persona ganará muchas veces, pero también perderá un
poco más .
Quizás esto ya sea tan obvio, pero el artículo trata solo sobre juegos basados en la aleatoriedad, no sobre póker, cartas, ajedrez, etc. ¿Puede haber una "estrategia ganadora" en tales juegos aleatorios? Obviamente no, porque ni el hueso, ni la pelota, ni los boletos de lotería tienen memoria, y su comportamiento no depende de iteraciones previas. Por cierto, es importante recordar este momento: intuitivamente, habiendo perdido varias veces, una persona puede decidir que ahora "definitivamente" ganará. Por desgracia, no hay ruleta o dado, y no saben sobre el número de intentos anteriores, cada juego comienza esencialmente con una pizarra limpia.
Respondiendo la pregunta en el título del artículo: ¿es posible ganar juegos de azar? Como muestra la simulación, en principio es posible, la teoría de la probabilidad admite. Pero no por mucho tiempo: vale la pena comenzar a jugar la 2da, 3ra, ... enésima vez, ya que el balance baja. A la larga, es imposible ganar en el casino.
PD: Para aquellos que quieran experimentar, el código fuente en un archivo se presenta bajo el spoiler. Se puede ejecutar en el IDE de Python en línea, por ejemplo
aquí . Para probar la versión europea de la ruleta en lugar de la estadounidense, es suficiente cambiar 38 a 37 en el código.Esta simulación es bastante básica y no tiene en cuenta varios factores adicionales, como la cantidad de dinero que tiene un jugador o el límite de apuestas en un casino, aquellos que lo deseen pueden agregar todo esto de forma independiente. Bajo el spoiler, también puede ver una versión en video de este artículo.
Código fuente import random def craps(): point = 0 while True: val = shoot()