Bromas aparte, el tema es grave, peligro de incendio. Vamos Este es el tercer artículo de la serie, discute modelos para estimar la corriente máxima de la pista impresa, que en algunas situaciones es un parámetro determinante al elegir el grosor de las capas conductoras de la placa de circuito impreso.
En un artículo
anterior se decía que la elección del grosor de las capas de cobre de la placa de circuito impreso está determinada, en primer lugar, por el espacio libre mínimo requerido y el ancho mínimo del conductor, así como la corriente máxima que fluye a través del conductor. Estos parámetros pueden contradecirse entre sí: cuanto más delgada es la capa conductora, más pequeño se puede obtener el patrón topológico, pero más pequeña es la corriente máxima que puede soportar la ruta de impresión (ceteris paribus, el ancho del conductor, la frecuencia de corriente, el disipador de calor, etc.). La energía térmica Q liberada en la resistencia óhmica R de la pista impresa (calor Joule Q = I
2 Rt, donde I es la fuerza actual, t es el tiempo) hace que su temperatura aumente en relación con el medio ambiente, lo que lleva a un sobrecalentamiento del conductor y componentes relacionados, o, como último recurso, a quemar a una corriente limitante (corriente de fusión en inglés). La relación entre la corriente a través de la pista de impresión y el aumento de la temperatura depende de muchos parámetros y generalmente es difícil de imaginar, sin embargo, existen fórmulas que nos permiten hacer estimaciones preliminares.
Precio, Onderdonk y Brooks
Uno de los primeros intentos fue hecho por W.H. Pris (WHPreece). Recibió su dependencia empírica en un experimento de laboratorio en el que aumentó gradualmente la corriente a través del conductor hasta que se ilumina en rojo. La fórmula de Pris relaciona la corriente luminosa con el diámetro del conductor d para varios materiales:
donde K es una constante tabular aproximadamente igual a 80 para el cobre. Usando la razón del área del círculo, podemos reescribir esta fórmula para el caso de un conductor de cobre con un área de sección transversal S:
En el experimento Pris, el conductor se suspendió en el aire, a diferencia de un conductor en una placa de circuito impreso, para el cual las condiciones del disipador de calor son completamente diferentes. Las condiciones del disipador de calor son más cercanas para los casos de un solo conductor de conexión, así como para algunos casos de soldadura de microhilos (cuando no se utiliza la combinación para protegerlo), donde esta fórmula puede proporcionar una buena estimación de la corriente limitante.
El aumento aceptable de la temperatura de la pista de impresión generalmente se considera de 10-30 ° C. Este valor puede ser mayor dependiendo de los parámetros del proyecto, sin embargo, en todo el rango de temperaturas de funcionamiento del producto, la temperatura de la pista debe ser menor que la temperatura de transición vítrea del material de la placa de circuito impreso (temperatura de transición vítrea inglesa, T
g ) y, más aún, la temperatura del brillo del cobre. Por lo tanto, la dependencia del aumento de temperatura ∆T de la corriente I de la pista impresa de ancho w y espesor de lámina h, útil por Brooks en [1], es útil:
donde C, α, β, γ son constantes, cuyos valores para las capas externa e interna se dan en la Tabla 1. Debe tenerse en cuenta que en las capas externas el espesor de la lámina suele ser 20-40 micras mayor que el valor base debido a la pulverización adicional al crear la transición agujeros Además, el efecto del acabado en tableros sin máscara puede ser significativo. Esto se usa en dispositivos de potencia, cuando se suelda una soldadura adicional a la pista impresa abierta desde la máscara.
Otra fórmula bien conocida para calcular la capacidad de carga de corriente máxima de un conductor es la fórmula de Onderdonk (inglés IMOnderdonk), que contiene un parámetro tan importante como el tiempo. Relaciona el tiempo t del paso de la corriente I a través de un conductor de cobre con una sección transversal S y el aumento de temperatura ∆T en relación con la temperatura inicial T
0 :
Dado que en la derivación de la fórmula [2] se excluye cualquier eliminación de calor, para el caso de una pista de impresión, esta fórmula es aplicable para un pulso de corriente corta que dura hasta 1-2 segundos. Con el aumento del tiempo y la influencia de la eliminación de calor, la precisión de la estimación disminuye, disminuyendo significativamente la corriente limitante. Los gráficos de dependencia para las tres fórmulas anteriores para varios parámetros de la pista de impresión se muestran en las Figuras 1 y 2.
Siempre es importante considerar las condiciones experimentales o los supuestos analíticos en la derivación para comprender los límites de aplicabilidad de una fórmula particular. Ninguna de las fórmulas anteriores proporcionará una relación exacta y óptima entre la corriente limitante y la sección transversal requerida del conductor para aplicaciones reales. Lo mismo se aplica a las calculadoras simples que se pueden encontrar en Internet (
por ejemplo ), porque se basan en estas o en fórmulas similares. La influencia de los conductores y componentes vecinos como fuentes y receptores de calor, radiación, enfriamiento activo o pasivo solo se puede tener en cuenta durante el modelado termoeléctrico en sistemas CAD especializados (como Cadence, ANSYS y otros). Sin embargo, incluso en este caso, los resultados del modelado y el experimento pueden variar significativamente. El hecho es que la pista de impresión no tiene una sección rectangular, sino que está cerca de la trapezoidal (Fig. 3), y su ancho y el valor de conductividad de la lámina de cobre no solo pueden diferir de los calculados por el modelo, sino que también tienen algo de dispersión de muestra a muestra, lote a lote, fabricante a fabricante, etc. La influencia de las desviaciones del ancho aumenta con su disminución. Sin embargo, los resultados calculados por fórmulas y recomendaciones de los estándares representarán con mayor frecuencia el peor de los casos, proporcionando así un margen de seguridad para el sistema. Si el desarrollador necesita optimizar la relación entre la corriente limitante y la sección transversal requerida de la pista impresa, entonces es necesario llegar a este objetivo mediante una forma iterativa de modelado y experimentación.

Efecto de la piel
Un aumento en la sección transversal de la pista impresa reduce proporcionalmente su resistencia óhmica por unidad de longitud, lo que reduce la pérdida de calor durante el flujo de corriente continua. La situación con corriente alterna no es tan simple debido a la existencia de un efecto de piel (efecto de piel inglés), lo que lleva al hecho de que la densidad de la corriente alterna se distribuye de manera desigual sobre la sección transversal del conductor, disminuyendo exponencialmente a cero desde la superficie del conductor hasta el centro. Para la conveniencia de los cálculos, se utiliza el concepto de la sección efectiva del conductor con una profundidad determinada por la relación:
donde f es la frecuencia actual, σ es la conductividad del metal, μ es la permeabilidad magnética. A una profundidad igual a δ, la densidad de corriente se vuelve e veces menor que la densidad de corriente en la superficie J
S. Matemáticamente, se puede mostrar la siguiente igualdad aproximada para la densidad de corriente J (x, y) en el conductor:
Es decir, para cálculos aproximados, podemos suponer que la corriente fluye solo en la capa límite del conductor perimetral l de profundidad δ, y con una distribución uniforme (Fig. 4).

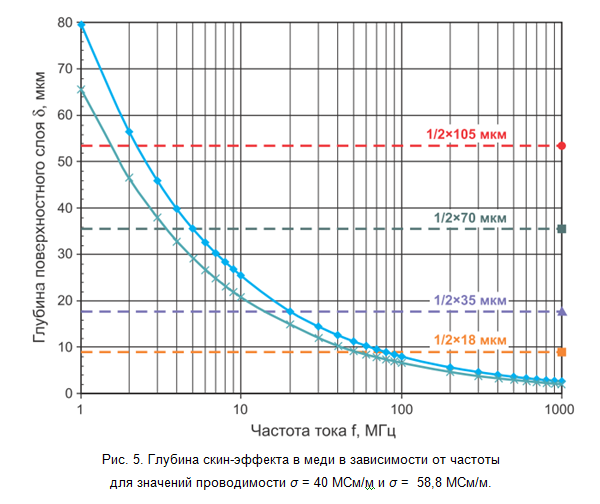
En el marco de este modelo simplificado, si la profundidad de la capa superficial es inferior a la mitad del grosor de la pista de impresión, esta sección efectiva determinará la impedancia de la pista de impresión a una frecuencia dada, lo que conducirá a un aumento de la resistencia óhmica y una ligera disminución de la inductancia. En la fig. La figura 5 muestra la dependencia de la profundidad de la capa superficial con la frecuencia de la corriente, teniendo en cuenta la dispersión en la conductividad del cobre depositado. Se puede ver de él que para las capas de cobre de 18 μm de espesor, la frecuencia de corte (por encima de la cual el efecto de la piel juega un papel) está en la región de 50-70 MHz, y para las capas de 35 μm de espesor está en la región de 15-20 MHz. Tenga en cuenta que a frecuencias superiores a 100 MHz, la profundidad del efecto de la piel varía ligeramente, esto nos permite descuidar su dependencia de la frecuencia en los cálculos de las señales de alta frecuencia.
Al diseñar placas de circuito impreso con corrientes constantes de varios amperios, es necesario realizar cálculos térmicos tanto para los componentes eléctricos como para los conductores. Los modelos presentados y las relaciones analíticas nos permiten estimar la corriente máxima de las pistas impresas y, sobre la base, seleccionar el grosor necesario de las capas de cobre y la topología de los conductores. Para obtener la solución exacta, es necesario utilizar sistemas CAD especializados, mientras que es deseable especificar la geometría teniendo en cuenta los errores de fabricación y los datos de conductividad del cobre recibidos del fabricante de las placas de circuito impreso. Recomiendo leer los
artículos de D. Brooks dedicados a un análisis detallado de los métodos para estimar la temperatura de los conductores impresos, que proporcionan resultados visuales de modelado de campos de temperatura.
Literatura
[1] Brooks DG, Adam J. "Traza corrientes y temperaturas revisadas", UltraCAD, 2015.
[2] Adam J., Brooks DG, "En busca de Preece y Onderdonk", UltraCAD, 2015.
El artículo fue publicado por primera vez en la revista Components and Technologies 2018, No. 1. La publicación en Geektimes ha sido acordada con los editores de la revista.