¿Qué tareas son adecuadas para la investigación científica?

¿Qué número debe insertarse en el último triángulo?

Los científicos resuelven problemas; Tal es su trabajo. Pero, ¿qué tareas serán temas de investigación prometedores? Para responder a esta pregunta, escribí el libro Lost in Mathematics , donde examiné problemas relacionados con los conceptos básicos de la física.

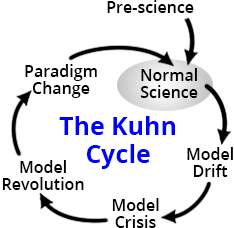
La primera clasificación aproximada de los problemas de investigación puede organizarse utilizando el ciclo de desarrollo de las teorías científicas de Thomas Kuhn. El ciclo de Kuhn consiste en una fase de "ciencia ordinaria", seguida de una "crisis" que conduce a un cambio de paradigma, después del cual comienza una nueva fase de "ciencia ordinaria". Esta es una simplificación increíble de la realidad, pero es adecuada para el razonamiento posterior.

Tareas comunes

Durante la fase científica ordinaria, las preguntas de investigación generalmente se pueden formular como "¿Cómo mediríamos esto?" (para los experimentadores) y "¿Cómo calcularíamos esto?" (para teóricos).



Los fundamentos de la física están llenos de tales "problemas ordinarios". Los experimentadores tienen muchos problemas, porque todos los problemas fáciles de resolver ya se han resuelto, y la complejidad de medir algo nuevo está en constante crecimiento. Los problemas de los teóricos se derivan del hecho de que las predicciones en física no se salen de las hipótesis por sí mismas. A menudo se requiere pasar por muchas etapas de argumentación y hacer muchos cálculos largos para llegar a las consecuencias numéricas de los supuestos teóricos.

Un buen ejemplo de un problema común en los fundamentos de la física sería la materia oscura fría. La hipótesis es bastante simple: en el espacio hay algo frío y oscuro que se comporta como un líquido e interactúa débilmente consigo mismo y con otra materia. Pero esto en sí mismo no es una predicción particularmente útil. Una buena tarea de investigación sería: "¿Cómo afecta la materia oscura fría a las fluctuaciones de temperatura del CMB?" Y luego viene la pregunta experimental: "¿Cómo medimos esto?"

Otras tareas de este tipo en los fundamentos de la física son: "¿Cuál es la contribución de la gravedad al momento magnético de un muón?" y "¿Cuál es el trasfondo de la dispersión de fotones en el Gran Colisionador de Hadrones?"

Las respuestas a tales tareas comunes amplían nuestra comprensión de las teorías existentes. Estos cálculos se pueden hacer dentro de nuestras plataformas existentes, pero pueden ser bastante complicados.

Las tareas dadas en los párrafos anteriores como ejemplos están resueltas, o al menos sabemos cómo resolverlas, aunque siempre es posible requerir una precisión mejorada. Pero en esta categoría también hay problemas sin resolver.

Por ejemplo, la teoría cuántica de la interacción nuclear fuerte debería predecir las masas de partículas que consisten en varios quarks: neutrones, protones y otras partículas compuestas similares (pero inestables). Pero tales cálculos son muy complicados. Hoy se llevan a cabo utilizando programas informáticos complejos (cálculos reticulares) y aún así sus predicciones no son tan buenas. Una pregunta relacionada es cómo se comporta la materia nuclear en los núcleos de las estrellas de neutrones.

Estos son solo ejemplos seleccionados al azar de muchas preguntas abiertas de física, que son "problemas normales", que, como se cree, se pueden encontrar en el marco de las teorías que ya conocemos, pero creo que ilustran bien este tema.

Si vamos más allá de lo básico, entonces tenemos tareas normales como predecir los ciclos solares y el clima soleado: son complejos debido a la extrema no linealidad y la turbulencia parcial del sistema, pero no esperamos que entren en conflicto con las teorías existentes. Todavía hay superconductividad a alta temperatura, un fenómeno bien estudiado, pero teóricamente insuficientemente entendido, ya que tales materiales carecen de cuasipartículas. Y así sucesivamente.

Estas son las tareas que estudiamos cuando todo va de acuerdo al plan. Pero todavía hay tareas que, en principio, pueden cambiar paradigmas, tareas que informan la existencia de una "crisis" en la terminología de Kuhn.

Tareas de crisis

Las tareas de crisis obvias son observaciones que no pueden explicarse sobre la base de teorías bien conocidas.

No considero que la mayoría de las observaciones relacionadas con la materia oscura y la energía oscura sean de crisis. La mayoría de estos datos se pueden explicar bastante bien simplemente agregando dos componentes nuevos al presupuesto de energía del universo. Por supuesto, se quejará de que esto no nos dará una descripción microscópica, pero no tenemos datos para estructuras microscópicas, por lo tanto, aún no podemos formular el problema.

Pero algunas observaciones de la materia oscura pertenecen a la "crisis". Correlaciones inexplicables, patrones en galaxias, que son difíciles de explicar con la ayuda de la materia oscura fría, por ejemplo, la dependencia de Tully-Fisher , o la extraña capacidad de la materia oscura para rastrear la distribución de la materia. Para estas observaciones, no existe una explicación satisfactoria basada en teorías bien conocidas. La modificación de la gravedad explica con éxito algunos de ellos, pero plantea otros problemas. ¡Tanto por la crisis! Y me atrevo a decir que esta es una buena crisis, porque tenemos datos que mejoran cada día.

Este no es el único buen problema de observación de crisis que existe en los fundamentos de la física. Uno de los más antiguos, pero aún vivo y bien, es el momento magnético del muón . Tenemos una discrepancia de larga data entre las predicciones teóricas y las mediciones, que aún no se resuelve. Muchos teóricos consideran que esto es una señal de que no puede explicarse en el marco del Modelo Estándar y, por lo tanto, se requiere una teoría nueva y mejorada.

Hay un par de problemas similares y bastante persistentes. Por ejemplo, el experimento DAMA . En este experimento, los científicos están buscando materia oscura. Reciben una señal de una fuente desconocida con modulación anual, y la han seguido durante más de diez años. Definitivamente hay una señal, pero si resulta ser materia oscura, entonces el resultado entrará en conflicto con otros resultados experimentales. Como resultado, DAMA ve algo, pero nadie sabe exactamente qué.

Todavía hay observaciones desconcertantes del experimento LSND sobre oscilaciones de neutrinos que son inconsistentes con cualquier otra combinación de parámetros. También hay una extraña discrepancia en los resultados de las mediciones del radio de protones utilizando dos métodos diferentes, así como otra historia similar con la vida útil del neutrón . También ha habido recientemente inconsistencias en la medición del parámetro Hubble utilizando diferentes métodos, y esto puede no valer la pena, pero puede valer la pena preocuparse.

Por supuesto, cada una de estas anomalías en los datos puede tener una explicación "normal". Esto puede ser un error de medición sistemático o un error de cálculo o un ingrediente faltante que contribuye. Pero quizás, quizás esto sea algo más.

Este es un tipo de "problema de crisis": el conflicto entre la teoría y la observación. Pero además de estos, hay problemas de crisis de un tipo completamente diferente, ubicados del lado del desarrollo de las teorías. Estos son problemas de consistencia interna.

El problema de la consistencia interna surge cuando su teoría predice observaciones conflictivas, ambiguas o sin sentido. Un ejemplo típico de esto son las probabilidades que se vuelven mayores que la unidad, que no coincide con la interpretación de la probabilidad. Debido a este problema, los físicos estaban convencidos de que el LHC nos demostraría una nueva física. No sabían si sería Higgs, y podría ser otra cosa, por ejemplo, un cambio inesperado en la interacción nuclear débil, pero resultó ser Higgs. La restauración de la consistencia interna condujo a una predicción exitosa.

Históricamente, el estudio de los problemas de coherencia ha dado lugar a muchos avances sorprendentes.

Un ejemplo de tal problema es la " catástrofe ultravioleta " en la que una fuente de calor tendría que emitir una cantidad infinita de luz a longitudes de onda cortas. Esto claramente no corresponde a una teoría física significativa en la cual las cantidades observadas deben ser finitas. (Tenga en cuenta que este conflicto surge con la suposición. Matemáticamente, no hay nada malo con el infinito). Planck resolvió este problema, y ​​la solución finalmente condujo al desarrollo de la mecánica cuántica.

Otro problema famoso con la consistencia es que la mecánica newtoniana resultó ser incompatible con la simetría de la electrodinámica del espacio-tiempo. Einstein resolvió este desacuerdo y recibió una teoría especial de la relatividad. Más tarde, Dirac resolvió la contradicción entre la mecánica cuántica y el STR, lo que llevó a la creación de la teoría cuántica de campos. Einstein eliminó las contradicciones adicionales entre SRT y la gravedad newtoniana, y recibió GR.

Todos estos problemas estaban bien definidos y especificados.

Pero la mayoría de los problemas teóricos actuales en los fundamentos de la física no son de este tipo. Sí, sería bueno si las tres interacciones del Modelo Estándar pudieran combinarse en una sola. Sería bueno, pero esto no es necesario para la coherencia. Sí, sería bueno si el Universo fuera supersimétrico. Sería bueno, pero esto no es necesario para la coherencia. Sí, sería bueno si pudiéramos explicar por qué la masa de Higgs no es técnicamente natural. Pero no hay contradicción en el hecho de que la masa de Higgs es lo que es.

El hecho de que Einstein, y aún más Dirac, se inspiraron en la belleza de sus teorías está bien descrito. A Dirac le gustaba especialmente elogiar el uso de la elegancia matemática en el desarrollo de las teorías. Pero su motivación personal nos interesa en la medida en que. Mirando hacia atrás, entendemos que han tenido éxito porque inicialmente asumieron buenas tareas.

Hay pocos problemas teóricos reales en los fundamentos de la física actual, pero existen. Una de ellas es la falta de cuantización de la gravedad. Es matemáticamente imposible simplemente juntar el Modelo Estándar y la Relatividad General, y no sabemos cómo hacerlo correctamente.

Otro problema grave con el modelo estándar es el polo Landau en una de las constantes de acoplamiento . Esto significa que la fuerza de una de las interacciones se vuelve infinita. Este no es un resultado físico, al igual que un desastre ultravioleta, por lo que algo debe suceder aquí. Se ha dedicado poca atención a este problema, ya que la mayoría de los teóricos creen que el modelo estándar se une mucho antes de alcanzar el polo de Landau, lo que hace que la extrapolación sea redundante.

Todavía hay casos en los que no está claro con qué tipo de tarea estamos trabajando. Una de ellas es la no convergencia de la expansión perturbativa. Quizás la única pregunta es mejorar el aparato matemático o, quizás, no entendemos completamente la teoría cuántica de campos. El mismo caso con el teorema de Haag . También es difícil para mí clasificar el problema de medición en mecánica cuántica. Una apelación a los procesos macroscópicos en los axiomas de la teoría es incompatible con los ideales de los reduccionistas, pero, nuevamente, este no es un problema fundamental, sino una preocupación conceptual. Entonces, sobre este problema, estoy en dificultades.

Sin embargo, la lección que nos enseña la historia de los problemas de crisis es clara: los problemas son temas de investigación prometedores si realmente son problemas. Es decir, debe ser capaz de formular una contradicción matemática. Si el problema es simplemente que no te gusta un cierto aspecto de la teoría, entonces es probable que solo pierdas tu tiempo.