El fracaso de la elegante versión original de la estructura del universo.

Los ocho planetas de nuestro sistema solar y nuestro sol, observando la escala de sus tamaños, pero no la escala de sus órbitas. A simple vista, lo más difícil de ver es Mercurio. Todos los planetas se mueven en órbitas elípticas.

Las mejores teorías científicas son simples, sin complicaciones, predicen efectivamente los resultados de las observaciones y contienen elegancia interior. Las ecuaciones más simples de Newton F = ma y Einstein E = mc ² contienen información sobresaliente y nos permiten deducir mucho de ellas; Los modelos de quarks y la relatividad general son fáciles de describir, pero son teorías increíblemente profundas que controlan las interacciones entre partículas; ideas como la supersimetría, la teoría de la gran unificación y la teoría de cuerdas extienden las simetrías conocidas por la física a nuevos niveles. Aplicando nuevas técnicas matemáticas al Universo, estamos buscando una verdad más profunda en la realidad que nuestro nivel actual de comprensión.

El modelo original del "Universo elegante", Mysterium Cosmographicum [El secreto del universo de Kepler], era simétrico, hermoso y basado en las matemáticas, que no se habían aplicado antes. Pero nuestra historia de advertencia de cómo resultó ser un gran fracaso científico también.


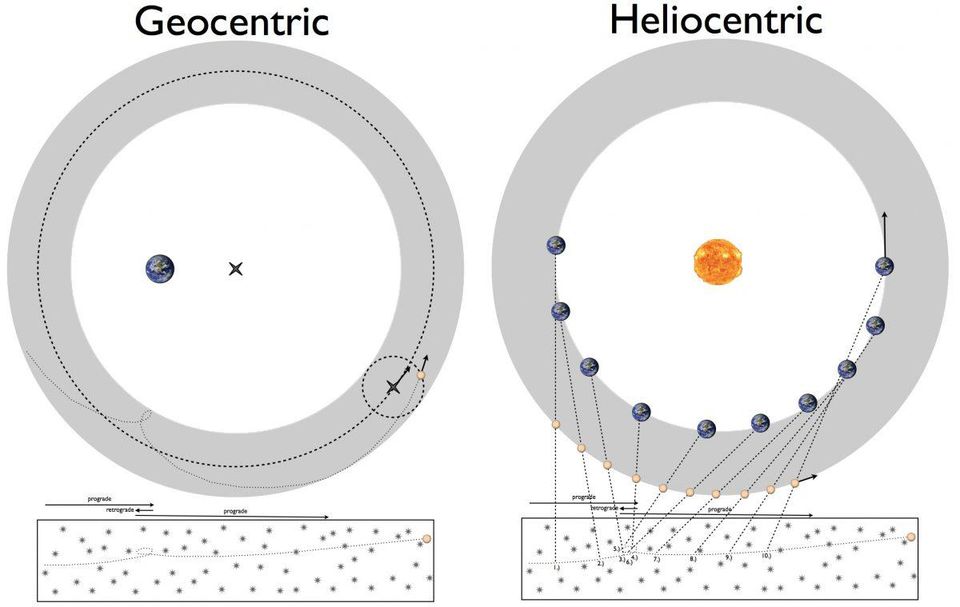Uno de los mayores misterios del siglo XVI fue cómo se mueven los planetas. Esto podría explicarse utilizando el modelo geocéntrico de Ptolomeo (izquierda) o el modelo heliocéntrico de Copérnico (derecha). Sin embargo, ninguno de ellos pudo calcular todos los detalles con precisión arbitraria.

Antes de Kepler, había tres sistemas principales que describían el Universo [el sistema solar en términos de ese tiempo]:

1. El modelo de Ptolomeo, en el que la Tierra estaba inmóvil, y todo giraba a su alrededor en un círculo, usaba equivalentes , deferentes y epiciclos .
2. El modelo copernicano, en el que el Sol estaba inmóvil y la Tierra era uno de los seis planetas que lo orbitaban, también usaba epiciclos.
3. El modelo Tycho Brahe, o geo-heliocéntrico , en el que el Sol giraba alrededor de la Tierra, y todos los demás planetas alrededor del Sol en círculos, también usando epiciclos.

Kepler, creando trabajo científico décadas antes que Galileo, pensó que los sistemas heliocéntricos eran prometedores, pero necesitaban más que solo círculos. Su apoyo requería una elegante estructura matemática. En un ataque de genio, con solo 24 años, Kepler publicó una idea que consideraba la más bella de sus ideas.


Kepler decidió que debería haber exactamente seis planetas en el sistema solar con órbitas definidas con precisión ubicadas en esferas inscritas en poliedros regulares

Dado que seis planetas giraron alrededor del Sol (todo más allá de Saturno solo se descubrirá 200 años después), Kepler decidió que debería haber seis órbitas únicas: una para cada uno de los planetas. ¿Pero por qué seis? ¿Por qué no más, por qué no menos? ¿Por qué hay tales distancias entre ellos? La conexión entre las órbitas y las matemáticas se convirtió en su idea de un universo elegante:

Planeo demostrar que Dios, creando el universo y colocando las esferas, tenía en mente cinco poliedros geométricos regulares, y limitó los tamaños, las proporciones y el movimiento de las esferas a sus tamaños.

Verá, en tres dimensiones puede crear exactamente cinco poliedros a partir de polígonos regulares, ni más ni menos. Fueron descubiertos por los antiguos griegos hace 2000 años, y a veces se les llama poliedros platónicos (aunque fueron descubiertos mucho antes que Platón). Kepler imaginó un sistema de esferas anidadas descritas e inscritas alrededor de cada uno de los poliedros, dando como resultado seis órbitas esféricas a lo largo de las cuales se mueven los planetas.


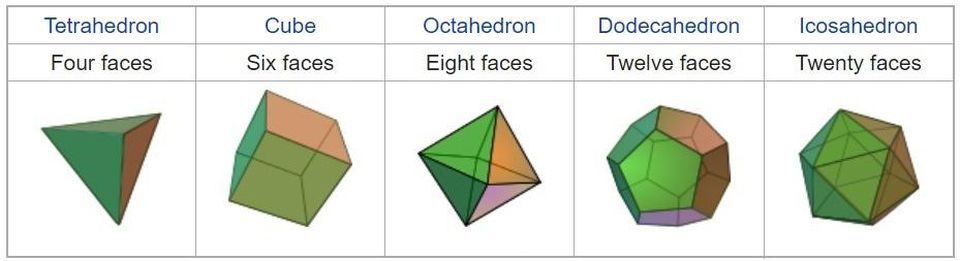Tetraedro, hexaedro (cubo), octaedro, dodecaedro, icosaedro. Cinco poliedros regulares, polígonos compuestos y regulares.

La esfera de Mercurio debe ser la más interna, y se encuentra dentro del octaedro, un poliedro regular, que consta de ocho triángulos equiláteros. A su alrededor, se describe la esfera de Venus; también está inscrita en el icosaedro, una figura de 20 lados que consiste en triángulos equiláteros. A su alrededor se describe la esfera de la Tierra inscrita en el dodecaedro, de las cuales 12 caras son pentágonos. A su alrededor se describe la esfera de Marte inscrita en un tetraedro: un poliedro tetraédrico con lados en forma de triángulos equiláteros. Alrededor del tetraedro se describe la esfera de Júpiter, inscrita en un cubo, el polígono resultante. Y a su alrededor se describe la última esfera, con la órbita de Saturno.


Según la teoría de Kepler, los radios relativos de las órbitas de los planetas se pueden calcular fácilmente. Sin embargo, la teoría no nació de la observación (obviamente, la discrepancia entre las esferas de Júpiter y Marte con el tetraedro), y Kepler tuvo que descartarla.

La idea de Kepler era realmente brillante; basado en ello, fue posible calcular con precisión la relación de los radios de todas las órbitas. El problema se reveló al comparar cálculos con observaciones. Las proporciones de los radios calculados de las órbitas de Mercurio y Venus, Venus y la Tierra, la Tierra y Marte estaban en buen acuerdo con la realidad, pero los dos últimos mundos no pudieron cumplir con los radios predichos por Kepler. En particular, el modelo fue refutado por la órbita de Marte, que no correspondía a ningún círculo. Y aunque Kepler continuó trabajando en ello, e incluso publicó la segunda edición 20 años después, su contribución más notable fue lo que la mayoría de los científicos no pueden hacer: abandonar su querida hipótesis.


Las órbitas de los planetas del sistema solar interior no son enteramente circulares, sino cercanas, y la mayoría se desvían del círculo de Mercurio y Marte. Además, los cometas y los asteroides se mueven a lo largo de elipses, obedeciendo el resto de las leyes de Kepler, si solo están conectados gravitacionalmente con el Sol.

Pero no fueron las esferas anidadas, sino las elipses las que lograron predecir correctamente el movimiento de los planetas. Las tres leyes de Kepler , sobre el movimiento de los planetas a lo largo de elipses alrededor del Sol, en áreas iguales descritas por radios para intervalos de tiempo iguales, y sobre la igualdad de las razones de los cuadrados de los períodos de revolución de los planetas y los cubos de los ejes semi-mayores de sus órbitas, fueron refutadas y reemplazadas por Mysterium Cosmographicum. El éxito de las órbitas elípticas allanó el camino para la ley de Newton de la gravitación universal y generó la astrofísica. A pesar del amor constante de Kepler por la idea más brillante, el universo fue mejor descrito por un modelo menos elegante. Después de dejar a un lado sus esperanzas y dejar que los datos experimentales se comporten aún más, fue capaz de lograr avances que la mente menos dotada no notaría.


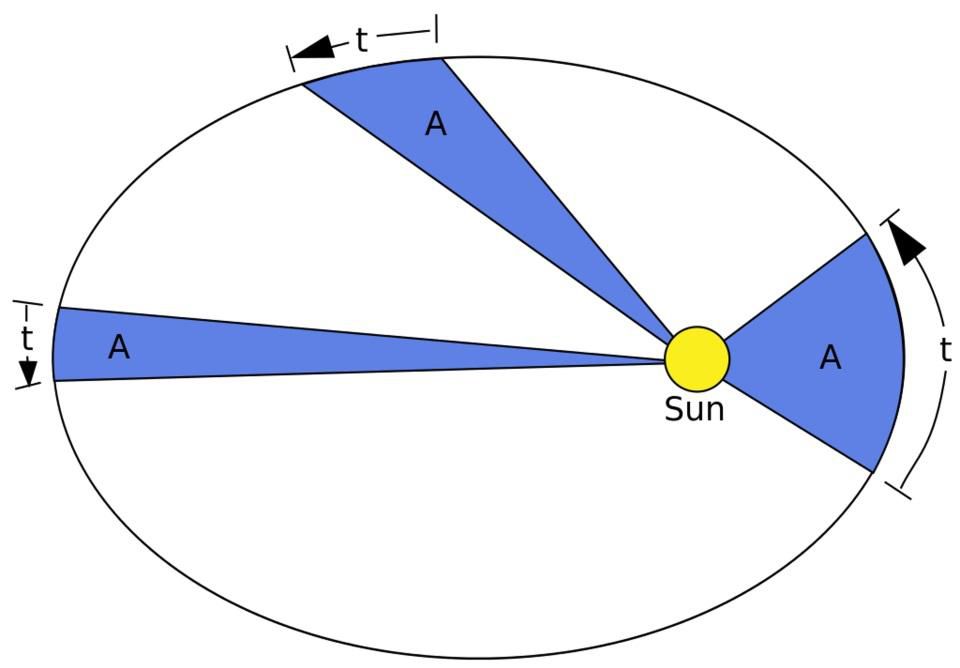Las tres leyes de Kepler se aplican a cualquier sistema gravitacional, así como al sistema solar.

En física, existe la tentación de sucumbir al reduccionismo: describir tantos fenómenos como sea posible con la menor cantidad de medios posible. La idea de la existencia de una teoría de todo, la única teoría capaz de predecir y describir todo lo que se puede describir o predecir en el Universo con la mayor precisión posible, es el sueño y el objetivo final de muchos científicos. Sin embargo, no hay garantía de que tal sueño pueda hacerse realidad en principio. Como escribió el famoso físico Lincoln Wulfenstein:

La lección de Kepler no es que debamos abstenernos de plantear preguntas aparentemente fundamentales; la lección es que no se nos da para averiguar si hay respuestas simples para ellos y dónde se pueden encontrar.

La elegancia, la belleza y el reduccionismo pueden abrir oportunidades increíbles para predicciones exitosas de nuevos fenómenos físicos, pero no hay garantía de que estas predicciones se hagan realidad. Haciendo un nuevo avance en la ciencia fundamental, muchos sueños comparten nuestros sueños y esperanzas de abordar la teoría unificadora de todo con la ayuda de la belleza matemática y la simetría adicional, pero nadie los garantiza. Que todos seamos tan abiertos al hecho de que nos cuentan los datos, como Kepler, y podemos seguirlos sin importar a dónde nos lleven.