En nuestro blog sobre Habré, publicamos traducciones adaptadas de materiales del blog The Financial Hacker, dedicadas a preguntas sobre la creación de estrategias para operar en el intercambio. Anteriormente, discutimos la
búsqueda de ineficiencias del mercado , la creación de
modelos de estrategias comerciales y los
principios de su programación . Hoy nos
centraremos en el uso de enfoques de aprendizaje automático para mejorar la eficiencia de los sistemas comerciales.
La primera computadora en ganar el Campeonato Mundial de Ajedrez fue Deep Blue. Eso fue en 1996, y pasaron otros veinte años antes de que otro programa, Alpha Go, lograra derrotar al mejor jugador en Go. Deep Blue era un sistema orientado a modelos con reglas de ajedrez integradas. AplhaGo es un sistema de minería de datos, una red neuronal profunda, entrenada utilizando miles de juegos en Go. Es decir, para dar un paso más allá de las victorias sobre las personas que son campeones en ajedrez, para dominar a los mejores jugadores en Go, no era necesario una pieza de hierro mejorada, sino un avance en el campo del software.
En el artículo actual, consideraremos aplicar el enfoque de minería de datos para crear estrategias comerciales. Este método no tiene en cuenta los mecanismos del mercado; simplemente escanea las curvas de precios y otras fuentes de datos para buscar patrones predictivos. El aprendizaje automático o la "inteligencia artificial" no siempre son necesarios para esto. Por el contrario, muy a menudo, los métodos más populares y rentables de minería de datos funcionan sin ningún tipo de adorno en forma de redes neuronales o soporte para métodos vectoriales.
Principios de aprendizaje automático
El algoritmo entrenado se alimenta con muestras de datos, generalmente extraídos de alguna manera de los precios de cambio históricos. Cada muestra consta de n variables x1 ... xn, que generalmente se denominan predictores, funciones, señales o, más simplemente, datos de entrada. Estos predictores pueden ser los precios de las últimas n barras en el gráfico de precios o un conjunto de valores de indicadores clásicos, o cualquier otra función de la curva de precios (¡incluso hay casos en los que se utilizan píxeles individuales del gráfico de precios como predictores para una red neuronal!). Cada muestra también suele contener una determinada variable objetivo y, por ejemplo, el resultado de la próxima transacción después de analizar la muestra o el siguiente movimiento de precios.
En la literatura, y a menudo se denomina etiqueta u objetivo. En el proceso de aprendizaje, el algoritmo aprende a predecir el objetivo y en función de los predictores x1 ... xn. Lo que el sistema "recuerda" en el proceso se almacena en una estructura de datos llamada modelo que es específico de un algoritmo particular (es importante no confundir este concepto con un modelo financiero o una estrategia orientada al modelo). Un modelo de aprendizaje automático puede ser funciones con reglas de predicción escritas usando el código C generado por el proceso de aprendizaje. O podría ser un conjunto de pesos relacionados con la red neuronal:
Entrenamiento: x1 ... xn, y => modelo
Predicción: x1 ... xn, modelo => y
Los predictores, funciones o como quiera llamarlos deben contener información suficiente para generar predicciones sobre el valor del objetivo y con cierta precisión. También deben cumplir con dos criterios formales. Primero, todos los valores predictores deben estar en el mismo rango, por ejemplo, -1 ... +1 (para la mayoría de los algoritmos en R) o -100 ... +100 (para algoritmos en los lenguajes de script Zorro o TSSB). Entonces, antes de enviar datos al sistema, debe normalizarlos. En segundo lugar, las muestras deben estar equilibradas, es decir, distribuidas de manera uniforme sobre los valores de la variable objetivo. Es decir, debe tener el mismo número de muestras que conducen a un resultado positivo y pierden series. Si no se siguen estos dos requisitos, los buenos resultados no tendrán éxito.
Los algoritmos de regresión generan predicciones sobre valores numéricos, como la magnitud o el signo del próximo movimiento de precios. Los algoritmos de clasificación predicen clases cuantitativas de muestras, por ejemplo, si preceden a la ganancia o pérdida de fondos. Algunos algoritmos, como las redes neuronales, los árboles de decisión o los métodos de vectores de soporte, se pueden ejecutar en ambos modos.
También hay algoritmos que pueden aprender a extraer de muestras de clase sin la necesidad de un objetivo y. Esto se llama aprendizaje no supervisado, en oposición al aprendizaje supervisado. En algún lugar entre estos dos métodos se encuentra el "aprendizaje de refuerzo", en el que el sistema se entrena ejecutando simulaciones con funciones específicas y utiliza el resultado como un objetivo. Un seguidor de AlphaGo, un sistema llamado AlphaZero utilizó aprendizaje reforzado, jugando un millón de juegos de Go consigo mismo. En finanzas, tales sistemas o productos que usan aprendizaje no supervisado son extremadamente raros. El 99% de los sistemas utilizan aprendizaje supervisado.
Cualesquiera que sean las señales que usamos para los predictores en finanzas, en la mayoría de los casos contendrán mucho ruido y poca información, y además serán inestables. Por lo tanto, la predicción financiera es una de las tareas más difíciles del aprendizaje automático. Algoritmos más complejos aquí logran mejores resultados. La selección de predictores es crítica para el éxito. No necesariamente debe haber muchos de ellos, ya que esto lleva a la reentrenamiento y el mal funcionamiento. Por lo tanto, las estrategias de minería de datos a menudo usan un algoritmo preseleccionado que extrae una pequeña cantidad de predictores de un grupo más amplio. Tal selección preliminar puede basarse en la correlación entre predictores, su importancia, riqueza de información o simplemente el éxito / fracaso del uso del conjunto de pruebas. Los experimentos prácticos con la selección de objetivos se pueden encontrar, por ejemplo, en el blog
Robot Wealth .
A continuación se muestra una lista de los métodos más populares de minería de datos utilizados en el campo de las finanzas.
1. Sopa de indicadores
La mayoría de los sistemas comerciales no se basan en modelos financieros. A menudo, los operadores solo necesitan señales comerciales generadas por ciertos indicadores técnicos, que se filtran por otros indicadores en combinación con indicadores técnicos adicionales. Cuando le pregunta a un comerciante acerca de cómo tal mezcla de indicadores puede generar algún tipo de beneficio, generalmente responde algo como: "Créeme, cambio mis manos y todo funciona".
Y es verdad Al menos a veces. Aunque la mayoría de estos sistemas no pasarán la
prueba WFA (y algunos simplemente prueban datos históricos), una cantidad sorprendentemente grande de dichos sistemas finalmente funciona y obtiene ganancias. El autor del blog Financial Hacker se dedica al desarrollo de sistemas de comercio personalizados y cuenta la historia de uno de los clientes que experimentó sistemáticamente con indicadores técnicos hasta que encontró una combinación que funciona para ciertos tipos de activos. Este método de prueba y error es un enfoque clásico para la minería de datos, para el éxito solo lo necesita, suerte y mucho dinero para las pruebas. Como resultado, a veces puede contar con obtener un sistema rentable.
2. Patrones de velas
No debe confundirse con los patrones de velas que han existido durante cientos de años. El equivalente moderno de este enfoque es el comercio basado en movimientos de precios. También analiza los indicadores de apertura, alto, bajo y cierre para cada vela en el gráfico. Pero ahora está utilizando la minería de datos para analizar las velas de la curva de precios para resaltar patrones que se pueden usar para generar predicciones sobre la dirección del movimiento de precios en el futuro.
Hay paquetes de software completos para este propósito. Buscan patrones que sean rentables en términos de criterios definidos por el usuario y los utilizan para crear una función de detección de patrones. Todo esto puede verse más o menos así:
int detect(double* sig) { if(sig[1]<sig[2] && sig[4]<sig[0] && sig[0]<sig[5] && sig[5]<sig[3] && sig[10]<sig[11] && sig[11]<sig[7] && sig[7]<sig[8] && sig[8]<sig[9] && sig[9]<sig[6]) return 1; if(sig[4]<sig[1] && sig[1]<sig[2] && sig[2]<sig[5] && sig[5]<sig[3] && sig[3]<sig[0] && sig[7]<sig[8] && sig[10]<sig[6] && sig[6]<sig[11] && sig[11]<sig[9]) return 1; if(sig[1]<sig[4] && eqF(sig[4]-sig[5]) && sig[5]<sig[2] && sig[2]<sig[3] && sig[3]<sig[0] && sig[10]<sig[7] && sig[8]<sig[6] && sig[6]<sig[11] && sig[11]<sig[9]) return 1; if(sig[1]<sig[4] && sig[4]<sig[5] && sig[5]<sig[2] && sig[2]<sig[0] && sig[0]<sig[3] && sig[7]<sig[8] && sig[10]<sig[11] && sig[11]<sig[9] && sig[9]<sig[6]) return 1; if(sig[1]<sig[2] && sig[4]<sig[5] && sig[5]<sig[3] && sig[3]<sig[0] && sig[10]<sig[7] && sig[7]<sig[8] && sig[8]<sig[6] && sig[6]<sig[11] && sig[11]<sig[9]) return 1; .... return 0; }
Esta función C devuelve 1 cuando la señal coincide con uno de los patrones; de lo contrario, devuelve 0. El código largo parece indicar que esta no es la forma más rápida de buscar patrones. Es mejor utilizar un enfoque en el que no sea necesario exportar la función de detección, pero puede ordenar las señales según su importancia y ordenarlas. Un ejemplo de dicho sistema se puede encontrar
en el enlace .
¿Puede operar a precio de trabajo? Como en el caso anterior, este método no se basa en ningún modelo financiero racional. Al mismo tiempo, todos entienden que realmente ciertos eventos en el mercado pueden afectar a sus participantes, como resultado de lo cual surgen patrones predictivos a corto plazo. Pero el número de tales patrones no puede ser grande si estudia solo la secuencia de varias velas consecutivas en el gráfico. Luego, deberá comparar el resultado con los datos de las velas, que no están cerca, pero que, por el contrario, se seleccionan al azar durante un período de tiempo más largo. En este caso, obtendrá un número casi ilimitado de patrones, y se separará con éxito de los conceptos de realidad y racionalidad. Es difícil imaginar cómo se puede predecir el precio futuro en función de algunos de sus valores la semana pasada. A pesar de esto, muchos comerciantes trabajan en esta dirección.
3. regresión lineal
Una base simple para muchos algoritmos complejos de aprendizaje automático: para predecir la variable objetivo y utilizando una combinación lineal de predictores x1 ... xn.

Probabilidades: este es el modelo. Se calculan para minimizar la suma de las desviaciones cuadráticas entre los valores reales y, los valores de entrenamiento y los y pronosticados según la fórmula:

Para muestras distribuidas normalmente, la minimización es posible utilizando operaciones matriciales, por lo que no se requieren iteraciones. En el caso cuando n = 1 - con un solo predictor x, la fórmula de regresión se reduce a:
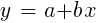
- es decir, antes de una regresión lineal simple, y cuando n> 1 la regresión lineal será multivariante. La regresión lineal simple está disponible en la mayoría de las plataformas de negociación, por ejemplo, el indicador
LinReg en TA-Lib. Cuando y = precio yx = tiempo, se puede usar como una alternativa a los promedios móviles. En la plataforma R, dicha regresión se implementa mediante la función de entrega estándar lm (..). También se puede representar por regresión polinómica. Como en el caso más simple, aquí usamos una variable predictiva x, pero también su cuadrado y grados posteriores, entonces xn == xn:
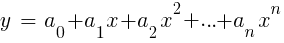
Si n = 2 o n = 3, la regresión polinómica se usa a menudo para predecir el próximo precio promedio a partir de los precios suavizados de las últimas barras. Para la regresión polinómica, se puede utilizar la función polyfit de MatLab, R, Zorro y muchas otras plataformas.
4. Perceptrón
A menudo se llama una red neuronal con una sola neurona. De hecho, el perceptrón es una función de regresión, como se describió anteriormente, pero con un resultado binario, como resultado de lo cual se llama
regresión logística . Aunque, en general, esto no es una regresión, sino un algoritmo de clasificación. Por ejemplo, la función de aviso (PERCEPTRON, ...) del marco Zorro genera un código C que devuelve 100 o -100 dependiendo de si el resultado predicho es umbral o no:
int predict(double* sig) { if(-27.99*sig[0] + 1.24*sig[1] - 3.54*sig[2] > -21.50) return 100; else return -100; }
Como puede ver, la matriz sig es equivalente a las funciones xn en la fórmula de regresión, y los coeficientes an son los factores digitales.
5. Redes neuronales
La regresión lineal o logística solo puede resolver problemas lineales. Al mismo tiempo, las tareas comerciales a menudo no encajan en esta categoría. Un ejemplo famoso es la predicción de la salida de una función XOR simple. Esto también incluye la predicción de ganancias de las transacciones. Una red neuronal artificial (ANN) puede resolver problemas no lineales. Este es un conjunto de perceptrones que están conectados en una matriz de diferentes niveles. Cada perceptrón es una neurona de red. Su salida se convierte en entrada a otras neuronas del siguiente nivel:
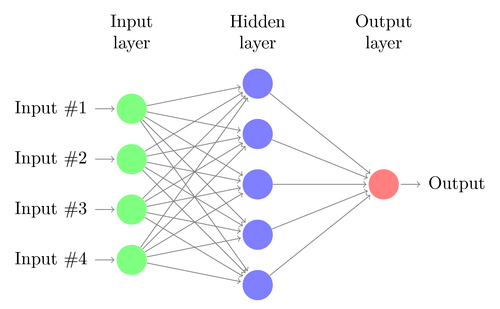
Al igual que el perceptrón, la red neuronal se entrena determinando coeficientes que minimizan el error entre la predicción y el objetivo en la muestra. Esto requiere un proceso de aproximación, generalmente con la propagación hacia atrás del error desde la salida a la entrada con la optimización de los pesos en el camino. Este proceso tiene dos limitaciones. Primero, la salida de neuronas debe ser una función continuamente diferenciable en lugar de un umbral simple para el perceptrón. En segundo lugar, la red no debe ser muy profunda: la presencia de una gran cantidad de niveles ocultos de neuronas entre los datos de entrada y salida solo perjudica. Esta segunda limitación limita la complejidad de los problemas que una red neuronal estándar puede resolver.
Cuando use redes neuronales para predecir transacciones, tendrá muchos parámetros que pueden manipularse, lo que, si se hace de manera incorrecta, puede dar como resultado un sesgo de selección (sesgo de selección):
- cantidad de niveles ocultos;
- la cantidad de neuronas en cada nivel oculto;
- número de ciclos de propagación hacia atrás - épocas;
- grado de entrenamiento, ancho de paso de la era;
- impulso, factor de inercia para la adaptación de pesas;
- función de activación
La función de activación emula el umbral del perceptrón. Para la propagación hacia atrás, necesita una función constantemente diferenciable que genere un paso suave para un cierto valor de x. Por lo general, para esto se utilizan las funciones sigmoide, tanh o softmax. A veces se utiliza una función lineal que devuelve la suma ponderada de todos los datos de entrada. En este caso, la red se puede utilizar para la regresión, la predicción de valores numéricos en lugar de la salida binaria.
Las redes neuronales se incluyen en la entrega de paquetes estándar de R (por ejemplo, nnet es una red con un nivel oculto), así como en muchos otros paquetes (como RSNNS y FCNN4R).
6. Aprendizaje profundo
Los métodos de aprendizaje profundo utilizan redes neuronales con muchos niveles ocultos y miles de neuronas que no pueden entrenarse de manera efectiva mediante la simple propagación de la espalda. En los últimos años, varios métodos se han vuelto populares para entrenar redes tan grandes. Por lo general, implican un entrenamiento previo de niveles ocultos de neuronas para aumentar la efectividad del aprendizaje básico.
La máquina de Boltzmann restringida (RBM) es un algoritmo de clasificación no controlado con una estructura de red especial en la que no hay conexiones entre las neuronas ocultas. Sparse Auto Encoder (SAE) utiliza la estructura de red habitual, pero pre-entrena niveles ocultos de una manera específica, reproduciendo señales de entrada en los niveles de salida con la menor cantidad de conexiones activas posible. Estos métodos le permiten implementar redes muy complejas para resolver problemas de aprendizaje muy complejos. Por ejemplo, la tarea de derrotar a la mejor persona que juega Go.
Las redes de aprendizaje profundo están incluidas en los paquetes deepnet y darch para R. Deepnet incluye el codificador automático, y darch incluye la máquina Boltzmann. A continuación se muestra un ejemplo de código que utiliza la red profunda con tres niveles ocultos para procesar señales comerciales a través de la función neor () del marco Zorro:
library('deepnet', quietly = T) library('caret', quietly = T) # called by Zorro for training neural.train = function(model,XY) { XY <- as.matrix(XY) X <- XY[,-ncol(XY)] # predictors Y <- XY[,ncol(XY)] # target Y <- ifelse(Y > 0,1,0) # convert -1..1 to 0..1 Models[[model]] <<- sae.dnn.train(X,Y, hidden = c(50,100,50), activationfun = "tanh", learningrate = 0.5, momentum = 0.5, learningrate_scale = 1.0, output = "sigm", sae_output = "linear", numepochs = 100, batchsize = 100, hidden_dropout = 0, visible_dropout = 0) } # called by Zorro for prediction neural.predict = function(model,X) { if(is.vector(X)) X <- t(X) # transpose horizontal vector return(nn.predict(Models[[model]],X)) } # called by Zorro for saving the models neural.save = function(name) { save(Models,file=name) # save trained models } # called by Zorro for initialization neural.init = function() { set.seed(365) Models <<- vector("list") } # quick OOS test for experimenting with the settings Test = function() { neural.init() XY <<- read.csv('C:/Project/Zorro/Data/signals0.csv',header = F) splits <- nrow(XY)*0.8 XY.tr <<- head(XY,splits) # training set XY.ts <<- tail(XY,-splits) # test set neural.train(1,XY.tr) X <<- XY.ts[,-ncol(XY.ts)] Y <<- XY.ts[,ncol(XY.ts)] Y.ob <<- ifelse(Y > 0,1,0) Y <<- neural.predict(1,X) Y.pr <<- ifelse(Y > 0.5,1,0) confusionMatrix(Y.pr,Y.ob) # display prediction accuracy }
7. Vectores de soporte
Al igual que con las redes neuronales, el método del vector de soporte es otra extensión de la regresión lineal. Si observa la fórmula de regresión nuevamente:

Entonces uno puede interpretar las funciones xn como las coordenadas de un espacio n-dimensional. Establecer la variable objetivo y en un valor fijo determinará el plano en este espacio; se llamará hiperplano, porque de hecho tendrá dos (incluso n-1) tamaños. El hiperplano separa las muestras con y> 0 de aquellas donde y <0. Los coeficientes an se pueden calcular como la ruta que separa el plano de las muestras más cercanas, sus vectores de soporte, de ahí el nombre del algoritmo. Por lo tanto, obtenemos un clasificador binario con la separación óptima de muestras ganadoras y perdedoras.
Problema: por lo general, estas muestras no se pueden dividir linealmente; se agrupan aleatoriamente en un espacio de funciones. Es imposible dibujar un plano suave entre las opciones ganadoras y perdedoras; si esto se pudiera hacer, para su cálculo se podrían usar métodos más simples como el análisis discriminante lineal. Pero en el caso general, puede usar el truco: agregar más tamaños al espacio. En este caso, el algoritmo de vector de soporte podrá generar más parámetros con una función nuclear que combine dos predictores, por analogía con la transición de la regresión simple al polinomio. Cuantos más tamaños agregue, más fácil será dividir las muestras con un hiperplano. Luego se puede volver a convertir al espacio n-dimensional original.
Al igual que las redes neuronales, los vectores de referencia pueden usarse no solo para la clasificación, sino también para la regresión. También ofrecen una serie de opciones para la optimización y posible reentrenamiento:
- Función del núcleo: generalmente se utiliza el núcleo RBF (función de base radial, núcleo simétrico), pero se pueden seleccionar otros núcleos, por ejemplo, sigmoides, polinomiales y lineales.
- Gamma: ancho del núcleo RBF.
- Parámetro de costo C, "penalización" por clasificaciones incorrectas de muestras de entrenamiento.
A menudo se usa la biblioteca libsvm, que está disponible en el paquete e1071 para R.
8. Algoritmo de vecinos k-más cercanos
En comparación con el pesado ANN y SVM, este es un algoritmo simple y agradable con una propiedad única: no necesita ser entrenado. Las muestras serán el modelo. Este algoritmo se puede usar para un sistema de comercio que se entrena constantemente agregando nuevas muestras. Este algoritmo calcula las distancias en el espacio de funciones desde el valor actual hasta las muestras k más cercanas. La distancia en el espacio n-dimensional entre los dos conjuntos (x1 ... xn) y (y1 ... yn) se calcula mediante la fórmula:
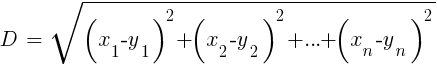
El algoritmo simplemente predice el objetivo a partir del promedio de k variables objetivo de las muestras más cercanas, ponderadas por sus distancias de retorno. Se puede usar tanto para clasificación como para regresión. Para predecir los vecinos más cercanos, puede llamar a la función knn en R o escribir el código C usted mismo para este propósito.
9. K-significa
Este es un algoritmo de aproximación para la clasificación no controlada. Es algo similar al algoritmo anterior. Para clasificar las muestras, el algoritmo primero coloca k puntos aleatorios en el espacio de funciones. Luego asigna a uno de estos puntos todas las muestras con la distancia más pequeña. Luego, el punto se desplaza a la mitad de estos valores más cercanos. Esto genera nuevos enlaces de muestra, ya que algunos de ellos ahora estarán más cerca de otros puntos. El proceso se repite hasta que se detiene la re-referencia como resultado del cambio de los puntos, es decir, hasta que cada punto sea promedio para las muestras más cercanas. Ahora tenemos k clases de muestra, cada una ubicada al lado de un punto k.
Este algoritmo simple puede producir resultados sorprendentemente buenos. En R, la función kmeans se usa para implementarla; se puede encontrar un ejemplo del algoritmo
en el enlace .
10. ingenuo Bayes
Este algoritmo utiliza el teorema bayesiano para clasificar muestras de funciones no numéricas (eventos), como los patrones de velas mencionados anteriormente. Suponga que el evento X (por ejemplo, el parámetro Open de la barra anterior debajo del parámetro Open de la barra actual) aparece en el 80% de las muestras ganadoras. Entonces, ¿cuál será la probabilidad de ganar la muestra en presencia del evento X en ella? Esto no es 0.8 como podría pensar. Esta probabilidad se calcula mediante la fórmula:
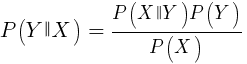
P (Y | X) es la probabilidad de que el evento Y (ganancia) ocurra en todas las muestras que contienen el evento X (en nuestro ejemplo, Open (1) <Open (0)). De acuerdo con la fórmula, es igual a la probabilidad de ocurrencia del evento X en todas las muestras ganadoras (en nuestro caso, 0.8), multiplicado por la probabilidad Y en todas las muestras (aproximadamente 0.5 si sigue los consejos para equilibrar las muestras) y dividido por la probabilidad de ocurrencia de X en todas las muestras
Si somos ingenuos y asumimos que todos los eventos de X son independientes entre sí, entonces podemos calcular la probabilidad total de que la muestra gane simplemente multiplicando las probabilidades P (X | ganar) para cada evento X. Luego llegamos a la siguiente fórmula:
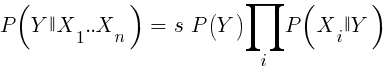
Con factor de escala s. Para que una fórmula funcione, las funciones deben elegirse de tal manera que sean lo más independientes posible. Esto será un obstáculo para usar ingenuos Bayes para el comercio. Por ejemplo, dos eventos Cerrar (1) <Cerrar (0) y Abrir (1) <Abrir (0) probablemente no sean independientes entre sí. Los predictores numéricos se pueden convertir en eventos dividiendo el número en rangos separados. Naive Bayes está disponible en el paquete e1071 para R.
11. Árboles de decisión y regresión
Dichos árboles predicen el resultado de valores numéricos basados en una cadena de decisión en el formato sí / no en la estructura de las ramas de los árboles. Cada decisión representa la presencia o ausencia de eventos (en el caso de valores no numéricos) o la comparación de valores con un umbral fijo. Una función de árbol típica, generada, por ejemplo, por el marco Zorro, se ve así:
int tree(double* sig) { if(sig[1] <= 12.938) { if(sig[0] <= 0.953) return -70; else { if(sig[2] <= 43) return 25; else { if(sig[3] <= 0.962) return -67; else return 15; } } } else { if(sig[3] <= 0.732) return -71; else { if(sig[1] > 30.61) return 27; else { if(sig[2] > 46) return 80; else return -62; } } } }
¿Cómo se obtiene tal árbol de un conjunto de muestras? Puede haber varios métodos para esto, incluida
la entropía informativa de Shannon .
Los árboles de decisión pueden ser ampliamente utilizados. Por ejemplo, son adecuados para generar predicciones que son más precisas de lo que se puede lograr utilizando redes neuronales o vectores de referencia. Sin embargo, esta no es una solución universal. El algoritmo más conocido de este tipo es C5.0, disponible en el paquete C50 para R.
Para mejorar aún más la calidad de las predicciones, puede utilizar conjuntos de árboles: se denominan bosques aleatorios. Este algoritmo está disponible en paquetes R llamados randomForest, ranger y Rborist.
Conclusión
Existen muchos métodos de minería de datos y aprendizaje automático. La pregunta crítica aquí es: ¿cuál es mejor, estrategias basadas en modelos o de aprendizaje automático? No hay duda de que el aprendizaje automático tiene una serie de ventajas. Por ejemplo, no necesita preocuparse por la microestructura del mercado, la economía, tener en cuenta la filosofía de los participantes del mercado u otras cosas similares. Puedes concentrarte en matemáticas puras. El aprendizaje automático es una forma mucho más elegante y atractiva de crear sistemas comerciales. Por su parte, todas las ventajas, excepto una, además de las historias en los foros de comerciantes, el éxito de este método en el comercio real es difícil de rastrear.
Casi todas las semanas, se publican nuevos artículos sobre el comercio mediante el aprendizaje automático. Dichos materiales deben tomarse con bastante escepticismo. Algunos autores afirman tasas ganadoras fantásticas de 70%, 80% o incluso 85%. Sin embargo, pocas personas dicen que puede perder dinero incluso si las predicciones están ganando. Una precisión del 85% generalmente se traduce en un indicador de rentabilidad superior a 5: si todo fuera tan simple, los creadores de dicho sistema ya se convertirían en multimillonarios. Sin embargo, por alguna razón, la reproducción de los mismos resultados simplemente repitiendo los métodos descritos en los artículos falla.
En comparación con los sistemas basados en modelos, hay muy pocos sistemas de aprendizaje automático realmente exitosos. Por ejemplo, rara vez son utilizados por fondos de cobertura exitosos. Quizás en el futuro, cuando la potencia informática se vuelva aún más accesible, algo cambie, pero hasta ahora los algoritmos de aprendizaje profundo siguen siendo más un pasatiempo interesante para los geeks que una herramienta real para ganar dinero en el intercambio.
Otros materiales financieros y bursátiles de ITI Capital :